Miningmodellinhalt von Zeitreihenmodellen (Analysis Services – Data Mining)
Gilt für: SQL Server 2019 und früheren Analysis Services
SQL Server 2019 und früheren Analysis Services  Azure Analysis Services
Azure Analysis Services  Fabric/Power BI Premium
Fabric/Power BI Premium
Wichtig
Data Mining wurde in SQL Server 2017 Analysis Services als veraltet eingestuft und wurde jetzt in SQL Server 2022 Analysis Services eingestellt. Die Dokumentation wird für veraltete und eingestellte Features nicht aktualisiert. Weitere Informationen finden Sie unter Abwärtskompatibilität von Analysis Services.
Zur Speicherung des Inhalts wird für alle Miningmodelle die gleiche Struktur verwendet. Diese Struktur wird nach dem Data Mining-Schemarowset für den Inhalt definiert. Innerhalb dieser standardmäßigen Struktur werden die Knoten, die Informationen enthalten, jedoch unterschiedlich angeordnet, sodass sie verschiedene Arten von Strukturen darstellen. In diesem Thema wird beschrieben, wie die Knoten organisiert sind und was jeder Knoten für Miningmodelle bedeutet, die auf dem Microsoft Time Series-Algorithmus basieren.
Eine Erläuterung des allgemeinen Miningmodellinhalts, der für alle Modelltypen gilt, finden Sie unter Miningmodellinhalt (Analysis Services – Data Mining).
Es empfiehlt sich, die Erläuterungen in diesem Thema anhand der Inhalte eines Zeitreihenmodells nachzuverfolgen. Sie können ein Zeitreihenmodell erstellen, indem Sie das Lernprogramm zu Data Mining-Grundlagen abschließen. Im Rahmen dieses Lernprogramms erstellen Sie ein gemischtes Modell, das zum Trainieren von Daten mit dem ARIMA- und dem ARTXP-Algorithmus dient. Informationen zum Anzeigen des Inhalts eines Miningmodells finden Sie unter Data Mining-Modell-Viewer.
Grundlegendes zur Struktur von Zeitreihenmodellen
Ein Zeitreihenmodell verfügt über einen einzigen übergeordneten Knoten, der das Modell und die zugehörigen Metadaten darstellt. Diesem Knoten sind eine oder zwei Zeitreihenstrukturen untergeordnet, je nachdem, welchen Algorithmus Sie verwendet haben, um das Modell zu erstellen.
Wenn Sie ein gemischtes Modell erstellen, werden zwei separate Strukturen hinzugefügt, eine für ARIMA und eine für ARTXP. Wenn Sie nur den ARTXP-Algorithmus oder nur den ARIMA-Algorithmus verwenden, wird eine einzelne Struktur hinzugefügt, die dem jeweiligen Algorithmus entspricht. Den zu verwendenden Algorithmus können Sie mit dem FORECAST_METHOD-Parameter festlegen. Weitere Informationen dazu, welches Modell Sie verwenden sollten, finden Sie unter Microsoft Time Series-Algorithmus.
Das folgende Diagramm zeigt ein Beispiel für ein Data Mining-Zeitreihenmodell mit den Standardeinstellungen zur Erstellung eines gemischten Modells. Für einen besseren Überblick über die Unterschiede zwischen den beiden Modellen wird das ARTXP-Modell auf der linken Seite und das ARIMA-Modell auf der rechten Seite des Diagramms gezeigt. Bei ARTXP handelt es sich um eine Baumstruktur mit immer detaillierter werdenden Verzweigungen, die mit dem ARIMA-Algorithmus erstellte Struktur ähnelt einer Pyramide, die von unten nach oben allgemeiner wird.
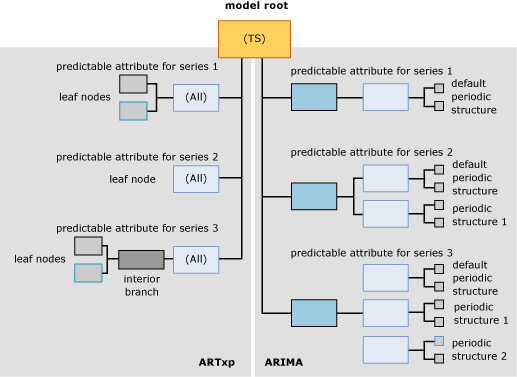
Sie müssen unbedingt beachten, dass die Informationen innerhalb der ARIMA-Struktur und der ARTXP-Struktur vollkommen unterschiedlich angeordnet werden und dass die beiden Strukturen nur über den Stammknoten verbunden sind. Obwohl die beiden Darstellungen der Einfachheit halber in einem Modell gezeigt werden, müssen Sie sie als zwei unabhängige Modelle behandeln. ARTXP entspricht im Gegensatz zu ARIMA einer tatsächlichen Baumstruktur.
Wenn Sie mit dem Microsoft Generic Content Tree Viewer ein Modell anzeigen, das ARIMA und ARTXP verwendet, werden die Knoten der ARTXP- und ARIMA-Modelle alle als untergeordnete Knoten des übergeordneten Zeitreihenmodells dargestellt. Sie können sie jedoch durch die angegebenen Knotenbezeichnungen leicht auseinanderhalten.
Die erste Knotengruppe wird mit (Alle) beschriftet und stellt die Ergebnisse der Analyse mit dem ARTXP-Algorithmus dar.
Die zweite Knotengruppe wird mit ARIMA beschriftet und stellt die Ergebnisse der Analyse mit dem ARIMA-Algorithmus dar.
Warnung
Die Bezeichnung (Alle) der ARTXP-Struktur wird lediglich aus Gründen der Abwärtskompatibilität beibehalten. Vor SQL Server 2008 wurde für den Time Series-Algorithmus nur der ARTXP-Algorithmus zur Analyse verwendet.
Die folgenden Abschnitte erklären, wie die Knoten innerhalb jedes dieser Modelltypen angeordnet sind.
Struktur des ARTXP-Modells
Mit dem ARTXP-Algorithmus wird ein Modell erstellt, das einem Entscheidungsstrukturmodell entspricht. Vorhersagbare Attribute werden gruppiert und immer dann geteilt, wenn signifikante Unterschiede gefunden werden. Aus diesem Grund enthält jedes ARTXP-Modell eine separate Verzweigung für jedes vorhersagbare Attribut. Im Lernprogramm zu Data Mining-Grundlagen wird beispielsweise ein Modell erstellt, das den Betrag der Verkäufe für mehrere Regionen vorhersagt. In diesem Fall ist [Amount] das vorhersagbare Attribut, und für jede Region wird eine separate Verzweigung erstellt. Bei zwei vorhersagbaren Attributen, z.B. [Amount] und [Quantity], wird für jede Attribut/Region-Kombination eine separate Verzweigung erstellt.
Der oberste Knoten der ARTXP-Struktur enthält dieselben Informationen wie der Stammknoten einer Entscheidungsstruktur. Dazu gehören die Anzahl der untergeordneten Elemente für diesen Knoten (CHILDREN_CARDINALITY), die Anzahl der Fälle, die die Bedingungen dieses Knotens erfüllen (NODE_SUPPORT), sowie verschiedene beschreibende Statistiken (NODE_DISTRIBUTION).
Wenn der Knoten keine untergeordneten Elemente hat, bedeutet dies, dass keine signifikanten Bedingungen gefunden wurden, die die weitere Unterteilung der Fälle rechtfertigen würden. Die Verzweigung endet an diesem Punkt, und der Knoten wird als Blattknotenbezeichnet. Der Blattknoten enthält die Attribute, Koeffizienten und Werte, aus denen sich die ARTXP-Formel zusammensetzt.
Einige Verzweigungen weisen möglicherweise zusätzliche Teilungen auf wie bei einem Entscheidungsstrukturmodell. Beispiel: Die Verzweigung einer Struktur, die die Verkäufe für die Region Europa darstellt, wird in zwei Verzweigungen unterteilt. Eine Teilung tritt auf, wenn eine Bedingung gefunden wird, die einen signifikanten Unterschied zwischen den zwei Gruppen darstellt. Der übergeordnete Knoten gibt den Namen des Attributs an, das die Teilung verursacht hat, z. B. [Amount], sowie die Anzahl der Fälle im übergeordneten Knoten. Die Blattknoten bieten weitere Details: den Wert des Attributs, z. B. [Sales] >10.000 vs. [Sales] < 10.000), die Anzahl der Fälle, die jede Bedingung unterstützen, und die ARTXP-Formel.
Hinweis
Sie finden die komplette Regressionsformel auf Blattknotenebene, jedoch nicht in Stamm- oder Zwischenebenenknoten.
Struktur eines ARIMA-Modells
Der ARIMA-Algorithmus erstellt eine einzelne Information für jede Kombination einer Datenreihe (z. B. [Region]) und eines vorhersagbaren Attributs (z. B. [Sales Amount]) – die Gleichung, die die Änderung des vorhersagbaren Attributs im Laufe der Zeit beschreibt.
Die Formel für jede Reihe wird von mehreren Komponenten abgeleitet, eine für jede in den Daten gefundene periodische Struktur. Wenn Sie beispielsweise über Verkaufsdaten verfügen, die auf monatlicher Basis erfasst werden, können mit dem Algorithmus monatliche, vierteljährliche oder jährliche periodische Strukturen erkannt werden.
Der Algorithmus gibt für jede gefundene Periodizität eine separate Gruppe übergeordneter und untergeordneter Knoten aus. Die Standardperiodizität ist 1 für eine einzelne Zeitscheibe. Diese wird automatisch allen Modellen hinzugefügt. Sie können mögliche periodische Strukturen angeben, indem Sie mehrere Werte im PERIODICITY_HINT-Parameter eingeben. Wenn der Algorithmus jedoch keine periodische Struktur erkennt, wird für die jeweilige Angabe kein Ergebnis ausgegeben.
Jede regelmäßige Struktur, die im Modellinhalt ausgegeben wird, enthält die folgenden Komponentenknoten:
Ein Knoten für die autoregressive Reihenfolge (AR)
Ein Knoten für den gleitenden Durchschnitt (MA)
Informationen zur Bedeutung dieser Begriffe finden Sie unter Microsoft Time Series-Algorithmus.
Die Differenzreihenfolge ist ein wichtiger Teil der Formel und wird in der Formel wiedergegeben. Weitere Informationen zur Verwendung der Differenzreihenfolge finden Sie unter Technische Referenz für den Microsoft Time Series-Algorithmus.
Modellinhalt eines Zeitreihenmodells
In diesem Abschnitt werden nur diejenigen Spalten des Miningmodellinhalts detaillierter und anhand von Beispielen erläutert, die für Zeitreihenmodelle relevant sind.
Informationen zu allgemeinen Spalten im Schemarowset, z. B. MODEL_CATALOG und MODEL_NAME, oder Erläuterungen zur Terminologie des Miningmodells finden Sie unter Miningmodellinhalt (Analysis Services – Data Mining).
MODEL_CATALOG
Name der Datenbank, in der das Modell gespeichert wird.
MODEL_NAME
Name des Modells.
ATTRIBUTE_NAME
Das vorhersagbare Attribut für die im Knoten dargestellte Datenreihe. (Der gleiche Wert wie für MSOLAP_MODEL_COLUMN.)
NODE_NAME
Der Name des Knotens.
Derzeit enthält diese Spalte den gleichen Wert wie NODE_UNIQUE_NAME. Dies ändert sich möglicherweise in zukünftigen Versionen.
NODE_UNIQUE_NAME
Der eindeutige Name des Knotens. Dem übergeordneten Knoten des Modells wird stets der Name TSzugewiesen.
ARTXP: Jeder Knoten wird durch TS gefolgt von einem hexadezimalen numerischen Wert dargestellt. Die Reihenfolge der Knoten ist hierbei nicht von Bedeutung.
Die der TS-Struktur direkt untergeordneten ARTXP-Knoten können beispielsweise die Bezeichnung TS00000001-TS0000000b aufweisen.
ARIMA: Jeder Knoten in der ARIMA-Struktur wird durch TA gefolgt von einem hexadezimalen numerischen Wert dargestellt. Die untergeordneten Knoten weisen den eindeutigen Namen des übergeordneten Knotens gefolgt von einer weiteren Hexadezimalzahl auf, mit der die Reihenfolge innerhalb des Knotens angegeben wird.
Alle ARIMA-Strukturen sind genau gleich strukturiert. Jedes Stammelement enthält die in der folgenden Tabelle dargestellten Knoten und Benennungskonvention:
| ARIMA-Knoten-ID und -Typ | Beispiel für Knotennamen |
|---|---|
| ARIMA-Stamm (27) | TA0000000b |
| ARIMA Periodische Struktur (28) | TA0000000b00000000 |
| ARIMA Autoregressiv (29) | TA0000000b000000000 |
| ARIMA Gleitender Durchschnitt (30) | TA0000000b000000001 |
NODE_TYPE
Ein Zeitreihenmodell gibt abhängig vom Algorithmus die folgenden Knotentypen aus.
ARTXP:
| Knotentyp-ID | Beschreibung |
|---|---|
| 1 (Model) | Zeitreihe |
| 3 (Innen) | Stellt eine Verzweigung innerhalb einer ARTXP-Zeitreihenstruktur dar. |
| 16 (Zeitreihenstruktur) | Stammelement der ARTXP-Struktur, das einem vorhersagbaren Attribut und einer Reihe entspricht. |
| 15 (Zeitreihe) | Blattknoten in der ARTXP-Struktur. |
ARIMA:
| Knotentyp-ID | Beschreibung |
|---|---|
| 27 (ARIMA-Stamm) | Der oberste Knoten einer ARIMA-Struktur. |
| 28 (ARIMA Periodische Struktur) | Komponente einer ARIMA-Struktur, die eine einzelne periodische Struktur beschreibt. |
| 29 (ARIMA Autoregressiv) | Enthält einen Koeffizienten für eine einzelne periodische Struktur. |
| 30 (ARIMA Gleitender Durchschnitt) | Enthält einen Koeffizienten für eine einzelne periodische Struktur. |
NODE_CAPTION
Eine Bezeichnung oder Beschriftung, die dem Knoten zugeordnet ist.
Diese Eigenschaft dient hauptsächlich zu Anzeigezwecken.
ARTXP: Enthält die Teilungsbedingung für den Knoten, die als Kombination aus Attribut und Wertebereich angezeigt wird.
ARIMA: Enthält die Kurzform der ARIMA-Formel.
Informationen über das Format der ARIMA-Formel finden Sie unter Mininglegende für die ARIMA-Formel.
CHILDREN_CARDINALITY
Die Anzahl der dem Knoten direkt untergeordneten Elemente.
PARENT_UNIQUE_NAME
Der eindeutige Name des dem Knoten übergeordneten Elements. Für Knoten auf der Stammebene wird NULL zurückgegeben.
NODE_DESCRIPTION
Eine Textbeschreibung der Regeln, Teilungen bzw. Formeln im aktuellen Knoten.
ARTXP: Weitere Informationen finden Sie unter Grundlegendes zur ARTXP-Struktur.
ARIMA: Weitere Informationen finden Sie unter Grundlegendes zur ARIMA-Struktur.
NODE_RULE
Eine XML-Beschreibung der Regeln, Teilungen bzw. Formeln im aktuellen Knoten.
ARTXP: NODE_RULE entspricht im Allgemeinen NODE_CAPTION.
ARIMA: Weitere Informationen finden Sie unter Grundlegendes zur ARIMA-Struktur.
MARGINAL_RULE
Eine XML-Beschreibung der knotenspezifischen Teilung bzw. des knotenspezifischen Inhalts.
ARTXP: MARGINAL_RULE entspricht im Allgemeinen NODE_DESCRIPTION.
ARIMA: Immer leer; verwenden Sie stattdessen NODE_RULE.
NODE_PROBABILITY
ARTXP: Für Strukturknoten immer 1. Für Blattknoten die Wahrscheinlichkeit für das Erreichen des Knotens vom Modellstammknoten aus.
ARIMA: Immer 0.
MARGINAL_PROBABILITY
ARTXP: Für Strukturknoten immer 1. Für Blattknoten die Wahrscheinlichkeit für das Erreichen des Knotens vom direkt übergeordneten Knoten aus.
ARIMA: Immer 0.
NODE_DISTRIBUTION
Eine Tabelle, die das Wahrscheinlichkeitshistogramm des Knotens enthält. In einem Zeitreihenmodell enthält diese geschachtelte Tabelle alle erforderlichen Komponenten für die tatsächliche Regressionsformel.
Weitere Informationen über die NODE_DISTRIBUTION-Tabelle in einer ARTXP-Struktur finden Sie unter Grundlegendes zur ARTXP-Struktur.
Weitere Informationen über die NODE_DISTRIBUTION-Tabelle in einer ARIMA-Struktur finden Sie unter Grundlegendes zur ARIMA-Struktur.
Sie können alle Konstanten und anderen Komponenten mit dem Time Series-Viewerin einem lesbaren Format anzeigen, indem Sie auf den Knoten klicken und die Mininglegendeöffnen.
NODE_SUPPORT
Die Anzahl der Fälle, die diesen Knoten unterstützen.
ARTXP: Gibt für den Knoten (Alle) die Gesamtzahl der in der Verzweigung enthaltenen Zeitscheiben an.
Gibt für Endknoten die Anzahl der Zeitscheiben an, die in dem mit NODE_CAPTION angegebenen Bereich enthalten sind. Die Anzahl der Zeitscheiben in den Endknoten wird stets zu dem NODE_SUPPORT-Wert des Knotens (Alle) addiert.
ARIMA: Eine Anzahl von Fällen, die die aktuelle periodische Struktur unterstützen. Der Unterstützungswert wird in allen Knoten der aktuellen periodischen Struktur wiederholt.
MSOLAP_MODEL_COLUMN
Das vorhersagbare Attribut für die im Knoten dargestellte Datenreihe. (Der gleiche Wert wie für ATTRIBUTE_NAME.)
MSOLAP_NODE_SCORE
Ein numerischer Wert, der den Informationswert der Struktur bzw. der Teilung kennzeichnet.
ARTXP: Für Knoten ohne eine Teilung ist der Wert immer 0.0. Für Knoten mit einer Teilung stellt der Wert den Interessantheitsgrad der Teilung dar.
Weitere Informationen zu Bewertungsmethoden finden Sie unter Featureauswahl (Data Mining).
ARIMA: Die BIC-Bewertung (Bayesian Information Criterion) des ARIMA-Modells. Dieser Wert wird für alle auf die Formel bezogenen ARIMA-Knoten festgelegt.
MSOLAP_NODE_SHORT_CAPTION
ARTXP: Dieselben Informationen wie die NODE_DESCRIPTION.
ARIMA: Dieselben Informationen wie bei NODE_CAPTION, d.h. die Kurzform der ARIMA-Formel.
Grundlegendes zur ARTXP-Struktur
Das ARTXP-Modell dient zur klaren Trennung der linearen Datenbereiche von den Datenbereichen, die nach anderen Faktoren unterteilt werden. Wenn die Änderungen im vorhersagbaren Attribut direkt als Funktion der unabhängigen Variablen dargestellt werden können, wird stets eine Regressionsformel zur Darstellung dieser Beziehung berechnet.
Beispiel: Wenn für die meisten Datenreihen eine direkte Korrelation zwischen Zeit- und Verkaufswerten besteht, ist jede Reihe in einer Zeitreihenstruktur (NODE_TYPE =16) enthalten, die keine untergeordneten Knoten für die einzelnen Datenreihen aufweist, sondern lediglich eine Regressionsformel. Wenn die Beziehung jedoch nicht linear ist, kann eine ARTXP-Zeitreihenstruktur anhand von Bedingungen in untergeordnete Knoten unterteilt werden wie bei einem Entscheidungsstrukturmodell. Wenn Sie den Modellinhalt im Microsoft Generic Content Tree Viewer anzeigen, sehen Sie, wo die Teilungen auftreten und welche Auswirkungen sie auf die Trendlinien haben.
Um dieses Verhalten besser zu verstehen, können Sie das im Lernprogramm zu Data Mining-Grundlagenerstellte Zeitreihenmodell überprüfen. Dieses Modell, das auf dem AdventureWorks-Data Warehouse basiert, verwendet keine besonders komplexen Daten. Aus diesem Grund weist die ARTXP-Struktur nur wenige Teilungen auf. Selbst in diesem relativ einfachen Modell sind jedoch drei unterschiedliche Teilungsarten dargestellt:
Die Trendlinie [Amount] für die Pazifikregion wird anhand des Zeitschlüssels unterteilt. Das heißt, der Trend ändert sich an einem bestimmten Zeitpunkt. Die Trendlinie ist bis zu einem bestimmten Punkt linear, danach nimmt die Kurve eine andere Form an. Beispiel: Eine Zeitreihe endet am 6. August 2002, und nach diesem Datum beginnt eine andere Zeitreihe.
Die Trendlinie [Amount] für Nordamerika wird anhand einer anderen Variablen unterteilt. In diesem Fall erfolgt die Unterteilung anhand des Werts für dasselbe Modell in der Region Europa. In anderen Worten: Der Algorithmus hat erkannt, dass bei Änderung des Werts für Europa der Wert für Nordamerika sich ebenfalls ändert.
Die Trendlinie für die Region Europa wird anhand von sich selbst unterteilt.
Welche Bedeutung haben die einzelnen Teilungen? Um den Modellinhalt richtig interpretieren zu können, müssen Sie mit den Daten und ihrer Bedeutung im geschäftlichen Zusammenhang bestens vertraut sein.
Die offensichtliche Verbindung zwischen den Trends für die Regionen Nordamerika und Europa bedeutet möglicherweise nur, dass die Datenreihe für Europa eine höhere Entropie aufweist, sodass der Trend für Nordamerika schwächer erscheint. Es kann aber auch sein, dass in der Bewertung der beiden Regionen kein signifikanter Unterschied besteht und die Korrelation zufällig erfolgte, da Europa vor Nordamerika berechnet wurde. Sie sollten die Daten auf jeden Fall überprüfen, um sich zu vergewissern, ob die Korrelation falsch ist oder ob möglicherweise andere Faktoren eine Rolle spielen.
Die Unterteilung anhand des Zeitschlüssels bedeutet, dass der Kurvenverlauf eine statistisch signifikante Änderung aufweist. Dies kann durch mathematische Faktoren verursacht werden, wie z. B. die Unterstützung für die einzelnen Reihen oder die für die Teilung erforderlichen Entropieberechnungen. Somit muss die Teilung für die Bedeutung des Modells in der Praxis nicht zwingend von Interesse sein. Beim Überprüfen des in der Teilung angegebenen Zeitraums finden Sie jedoch u. U. interessante Zusammenhänge, die in den Daten nicht dargestellt werden, wie z. B. eine Werbeaktion oder ein anderes Ereignis, das zu diesem Zeitpunkt beginnt und möglicherweise Auswirkungen auf die Daten hat.
Wenn die Daten andere Attribute enthielten, wären die Verzweigungsbeispiele für die Struktur interessanter. Beispiel: Wenn Sie Wetterinformationen erfassen und diese als Attribut für die Analyse verwenden, kann die Struktur mehrere Teilungen aufweisen, die den komplexen Zusammenhang zwischen Verkaufsdaten und Wetterdaten darstellen.
Kurz: Data Mining bietet nützliche Hinweise auf Phänomene, die potenziell von Interesse sind. Um den Wert der Informationen im Kontext genau interpretieren zu können, sind jedoch weitere Untersuchungen und geschäftliches Fachwissen erforderlich.
Elemente der ARTXP-Zeitreihenformel
Zum Anzeigen der vollständigen Formel für eine ARTXP-Struktur oder einen ArtXP-Branch empfiehlt es sich, die Mininglegende des Microsoft Time Series Viewers zu verwenden, die alle Konstanten in einem lesbaren Format darstellt.
Im folgenden Abschnitt werden eine Beispielformel und die grundlegenden Begriffe vorgestellt.
Mininglegende für ARTXP-Formel
Das folgende Beispiel zeigt die ARTXP-Formel für einen Teil des Modells, wie sie in der Mininglegendedargestellt wird. So zeigen Sie diese Formel an: Öffnen Sie das Modell [Forecasting], das Sie im Tutorial zu Data Mining-Grundlagen erstellt haben, im Microsoft Time Series-Viewer, und klicken Sie auf die Registerkarte Modell . Wählen Sie dann die Struktur für die Datenreihe „R250: Europe“ aus.
Um die für dieses Beispiel verwendete Formel anzuzeigen, klicken Sie auf den Knoten, der die Datenreihe am/nach dem 5.7.2003 darstellt.
Beispiel für Strukturknotenformel:
Quantity = 21.322 -0.293 * Quantity(R250 North America,-7) + 0.069 * Quantity(R250 Europe,-1) + 0.023 * Quantity(R250 Europe,-3) -0.142 * Quantity(R750 Europe,-8)
In diesem Fall stellt der Wert 21.322 den Wert dar, der für „Quantity“ als Funktion der folgenden Formelelemente vorhergesagt wird.
Ein Element lautet beispielsweise Quantity(R250 North America,-7). Hiermit wird die Menge für die Region Nordamerika bei t-7, also sieben Zeitscheiben vor der aktuellen Zeitscheibe, angegeben. Der Wert für diese Datenreihe wird mit dem Koeffizienten -0,293 multipliziert. Die Koeffizienten für die einzelnen Elemente werden während des Trainingsprozesses abgeleitet und basieren auf Trends in den Daten.
Diese Formel weist mehrere Elemente auf, da berechnet wurde, dass der Mengenwert des R250-Modells für die Region Europa von den Werten verschiedener anderer Datenreihen abhängt.
Modellinhalt einer ARTXP-Formel
In der folgenden Tabelle werden dieselben Informationen für die Formel unter Verwendung des Inhalts des relevanten Knotens angezeigt, wie sie im Microsoft Generic Content Tree Viewer (Data Mining) angezeigt werden.
| ATTRIBUTE_NAME | ATTRIBUTE_VALUE | Alias | PROBABILITY | Varianz | VALUETYPE |
|---|---|---|---|---|---|
| Quantity(R250 Europe,y-intercept) | 21.3223433563772 | 11 | 0 | 1.65508795539661 | 11 (Intercept) |
| Quantity(R250 Europe,-1) | 0.0691694140876526 | 0 | 0 | 0 | 7 (Koeffizient) |
| Quantity(R250 Europe,-1) | 20.6363635858123 | 0 | 0 | 182.380682874818 | 9 (Statistik) |
| Quantity(R750 Europe,-8) | -0.1421203048299 | 0 | 0 | 0 | 7 (Koeffizient) |
| Quantity(R750 Europe,-8) | 22.5454545333019 | 0 | 0 | 104.362130048408 | 9 (Statistik) |
| Quantity(R250 Europe,-3) | 0.0234095979448281 | 0 | 0 | 0 | 7 (Koeffizient) |
| Quantity(R250 Europe,-3) | 24.8181818883176 | 0 | 0 | 176.475304989169 | 9 (Statistik) |
| Quantity(R250 North America,-7) | -0.292914186039869 | 0 | 0 | 0 | 7 (Koeffizient) |
| Quantity(R250 North America,-7) | 10.36363640433 | 0 | 0 | 701.882534898676 | 9 (Statistik) |
Beim Vergleich dieser Beispiele wird deutlich, dass der Inhalt des Miningmodells den Informationen entspricht, die in der Mininglegendeverfügbar sind, jedoch mit den zusätzlichen Spalten VARIANCE und SUPPORT. Der Wert für SUPPORT gibt die Anzahl von Fällen an, die den mit dieser Formel beschriebenen Trend unterstützen.
Verwenden der ARTXP-Zeitreihenformel
Der Vorteil des ARTXP-Modells besteht für die meisten geschäftlichen Anwender darin, dass es eine Strukturansicht und eine lineare Darstellung der Daten kombiniert.
Wenn die Änderungen im vorhersagbaren Attribut als lineare Funktion der unabhängigen Variablen dargestellt werden können, berechnet der Algorithmus automatisch die Regressionsformel und gibt die Reihe in einem separaten Knoten aus.
Jedes Mal, wenn die Beziehung nicht als lineare Korrelation ausgedrückt werden kann, wird die Zeitreihe wie bei einer Entscheidungsstruktur verzweigt.
Wenn Sie im Microsoft Time Series-Viewer durch den Modellinhalt navigieren, sehen Sie, wo die Teilung auftritt und welche Auswirkung sie auf die Trendlinie hat.
Wenn in einem beliebigen Teil der Datenreihe eine direkte Korrelation zwischen Zeit- und Verkaufsdaten vorhanden ist, können Sie die Formel einfach aus der Mininglegendekopieren und in ein Dokument oder eine Präsentation einfügen, um das Modell besser zu erläutern. Sie haben auch die Möglichkeit, Mittelwert, Koeffizient und andere Informationen aus der Tabelle NODE_DISTRIBUTION für diese Struktur zu extrahieren und zur Berechnung von Trenderweiterungen zu verwenden. Wenn die gesamte Reihe eine konsistente lineare Beziehung aufweist, ist die Formel im Knoten (Alle) enthalten. Wenn die Struktur eine Verzweigung aufweist, ist die Formel im Blattknoten enthalten.
Die folgende Abfrage gibt alle ARTXP-Blattknoten aus einem Miningmodell sowie die geschachtelte Tabelle NODE_DISTRIBUTION zurück, die die Formel enthält.
SELECT MODEL_NAME, ATTRIBUTE_NAME, NODE_NAME,
NODE_CAPTION,
(SELECT ATTRIBUTE_NAME, ATTRIBUTE_VALUE, [VARIANCE], VALUETYPE
FROM NODE_DISTRIBUTION) as t
FROM Forecasting.CONTENT
WHERE NODE_TYPE = 15
Grundlegendes zur ARIMA-Struktur
Jede Struktur in einem ARIMA-Modell entspricht einer Periodizität oder periodischen Struktur. Eine periodische Struktur ist ein Datenmuster, das sich durch die gesamte Datenreihe zieht. Geringfügige Abweichungen in diesem Muster sind innerhalb statistischer Grenzen erlaubt. Die Periodizität wird nach den Standardzeiteinheiten gemessen, die in den Trainingsdaten verwendet wurden. Beispiel: Wenn die Trainingsdaten Verkaufsdaten für jeden Tag enthalten, ist die Standardzeiteinheit ein Tag, und alle periodischen Strukturen werden als Anzahl von Tagen definiert.
Jede periodische Struktur, die vom Algorithmus erkannt wird, erhält einen eigenen Strukturknoten. Wenn Sie z. B. Verkaufsdaten auf Tagesbasis analysieren, können periodische Strukturen erkannt werden, die Wochen darstellen. In diesem Fall erstellt der Algorithmus zwei periodische Strukturen im fertigen Modell: eine für den standardmäßigen täglichen Zeitraum, bezeichnet als {1}und eine für Wochen, die durch angegeben wird {7}.
Beispiel: Die folgende Abfrage gibt alle ARIMA-Strukturen aus einem Miningmodell zurück.
SELECT MODEL_NAME, ATTRIBUTE_NAME, NODE_NAME, NODE_CAPTION
FROM Forecasting.CONTENT
WHERE NODE_TYPE = 27
Beispielergebnisse:
| MODEL_NAME | ATTRIBUTE_NAME | NODE_NAME | NODE_TYPE | NODE_CAPTION |
|---|---|---|---|---|
| Vorhersagen | M200 Europe: Quantity | TA00000000 | 27 | ARIMA (1,0,1) |
| Vorhersagen | M200 North America:Quantity | TA00000001 | 27 | ARIMA (1,0,4) X (1,1,4)(6) |
| Vorhersagen | M200 Pacific:Quantity | TA00000002 | 27 | ARIMA (2,0,8) X (1,0,0)(4) |
| Vorhersagen | M200 Pacific:Quantity | TA00000002 | 27 | ARIMA (2,0,8) X (1,0,0)(4) |
| Vorhersagen | R250 Europe:Quantity | TA00000003 | 27 | ARIMA (1,0,7) |
| Vorhersagen | R250 North America:Quantity | TA00000004 | 27 | ARIMA (1,0,2) |
| Vorhersagen | R250 Pacific:Quantity | TA00000005 | 27 | ARIMA (2,0,2) X (1,1,2)(12) |
| Vorhersagen | R750 Europe:Quantity | TA00000006 | 27 | ARIMA (2,1,1) X (1,1,5)(6) |
| Vorhersagen | T1000 Europe:Quantity | TA00000009 | 27 | ARIMA (1,0,1) |
| Vorhersagen | T1000 North America:Quantity | TA0000000a | 27 | ARIMA (1,1,1) |
| Vorhersagen | T1`000 Pacific:Quantity | TA0000000b | 27 | ARIMA (1,0,3) |
Anhand dieser Ergebnisse, die Sie auch mit dem Microsoft Generic Content Tree Viewer (Data Mining) durchsuchen können, können Sie auf einen Blick erkennen, welche Reihen vollständig linear sind, welche mehrere periodische Strukturen aufweisen und wie die ermittelten Periodizitäten sind.
An der Kurzform der ARIMA-Formel für die Datenreihe M200 Europe können Sie z. B. ablesen, dass nur der standardmäßige Tageszyklus erkannt wurde. Die Kurzform der Formel wird in der Spalte NODE_CAPTION bereitgestellt.
Für die Reihe M200 North America wurde jedoch eine weitere periodische Struktur gefunden. Der Knoten TA00000001 verfügt über zwei untergeordnete Knoten, einen mit der Formel (1,0,4) und einen mit der Formel (1,1,4)(6). Diese Formeln werden verkettet und im übergeordneten Knoten angegeben.
Für jede periodische Struktur stellt der Modellinhalt außerdem die Reihenfolge und den gleitenden Durchschnitt in Form von untergeordneten Knoten bereit. So werden z. B. mit der folgenden Abfrage die untergeordneten Knoten von einem der im vorherigen Beispiel aufgelisteten Knoten abgerufen. Beachten Sie, dass die Spalte PARENT_UNIQUE_NAME in Klammern eingeschlossen werden muss, um sie von dem reservierten Schlüsselwort mit demselben Namen zu unterscheiden.
SELECT *
FROM Forecasting.CONTENT
WHERE [PARENT_UNIQUE_NAME] = ' TA00000001'
Da dies eine ARIMA-Struktur und keine ARTXP-Struktur ist, können Sie die IsDescendant-Funktion (DMX) nicht verwenden, um die untergeordneten Knoten dieser periodischen Struktur zurückzugeben. Stattdessen können Sie die Ergebnisse anhand von Attribut- und Knotentypen filtern, sodass die untergeordneten Knoten zurückgegeben werden, die zusätzliche Informationen zum Aufbau der Formel bereitstellen, wie z. B. gleitender Durchschnitt und Differenzreihenfolge.
SELECT MODEL_NAME, ATTRIBUTE_NAME, NODE_UNIQUE_NAME,
NODE_TYPE, NODE_CAPTION
FROM Forecasting.CONTENT
WHERE [MSOLAP_MODEL_COLUMN] ='M200 North America:Quantity'
AND (NODE_TYPE = 29 or NODE_TYPE = 30)
Beispielergebnisse:
| MODEL_NAME | ATTRIBUTE_NAME | NODE_UNIQUE_NAME | NODE_TYPE | NODE_CAPTION |
|---|---|---|---|---|
| Vorhersagen | M200 North America:Quantity | TA00000001000000010 | 29 | ARIMA {1,0.961832044807041} |
| Vorhersagen | M200 North America:Quantity | TA00000001000000011 | 30 | ARIMA {1,-3.51073103693271E-02,2.15731642954099,-0.220314343327742,-1.33151478258758} |
| Vorhersagen | M200 North America:Quantity | TA00000001000000000 | 29 | ARIMA {1,0.643565911081657} |
| Vorhersagen | M200 North America:Quantity | TA00000001000000001 | 30 | ARIMA {1,1.45035399809581E-02,-4.40489283927752E-02,-0.19203901352577,0.242202497643993} |
Diese Beispiele veranschaulichen, dass bei jedem weiteren Drilldown in der ARIMA-Struktur mehr Details aufgerufen werden, die wichtigen Informationen werden jedoch kombiniert und auch im übergeordneten Knoten angezeigt.
Zeitreihenformel für ARIMA
Verwenden Sie zur Anzeige der kompletten Formel für einen ARIMA-Knoten die Mininglegende im Microsoft Time Series-Viewer, in der die autoregressive Reihenfolge, der gleitende Durchschnitt und andere Elemente der Formel in einem konsistenten und lesbaren Format dargestellt werden.
Dieser Abschnitt enthält eine Beispielformel sowie Erläuterungen zu den grundlegenden Begriffen.
Mininglegende für ARIMA-Formel
Das folgende Beispiel zeigt die ARIMA-Formel für einen Teil des Modells, wie sie in der Mininglegende dargestellt wird. So zeigen Sie diese Formel an: Öffnen Sie das Forecasting -Modell im Microsoft Time Series-Viewer, und klicken Sie auf die Registerkarte Modell . Wählen Sie dann die Struktur für die Datenreihe R250: Europe aus, und klicken Sie auf den Knoten, der die Datenreihe am oder nach dem 5.7.2003 darstellt. In der Mininglegende werden alle Konstanten in einem lesbaren Format angezeigt, wie im folgenden Beispiel:
ARIMA-Formel:
ARIMA ({1,1},0,{1,1.49791920964142,1.10640053499397,0.888873034670339,-5.05429403071953E-02,-0.905265316720334,-0.961908900643379,-0.649991020901922}) Intercept:56.8888888888889
Dies ist das lange ARIMA-Format, das die Werte der Koeffizienten und das konstante Glied (Intercept) einschließt. Das kurze Format für diese Gleichung wäre {1,0,7}, wobei 1 den Zeitraum als Anzahl von Zeitsegmenten, 0 die Reihenfolge der Begriffsdifferenz und 7 die Anzahl der Koeffizienten angibt.
Hinweis
Zur Varianzberechnung wird von Analysis Services eine Konstante ermittelt, diese wird jedoch auf der Benutzeroberfläche nicht angezeigt. Sie können jedoch die Varianz für einen beliebigen Punkt in der Datenreihe als Funktion dieser Konstante anzeigen, indem Sie in der Diagramm -Sicht die Option Abweichungen anzeigen wählen. Die Varianz für spezifische vorhergesagte Punkte lässt sich in der QuickInfo zu jeder Datenreihe anzeigen.
Modellinhalt einer ARIMA-Formel
Ein ARIMA-Modell folgt einer Standardstruktur, bei der unterschiedliche Informationen in Knoten unterschiedlichen Typs enthalten sind. Um den Inhalt des ARIMA-Modells anzuzeigen, wechseln Sie zum Microsoft Generic Content Tree Viewer, und erweitern Sie den Knoten mit dem Attributnamen R250 Europe:Quantity.
Das ARIMA-Modell für eine Datenreihe enthält die grundlegende periodische Formel in vier verschiedenen Formaten, aus denen Sie das für Ihre Anwendung am besten geeignete Format auswählen können.
NODE_CAPTION: zeigt die Kurzform der Formel an. Aus der Kurzform ersehen Sie, wie viele periodische Strukturen dargestellt werden und wie viele Koeffizienten diese aufweisen. Wenn das Kurzformat der Formel z. B. {4,0,6}lautet, stellt der Knoten eine periodische Struktur mit 6 Koeffizienten dar. Wenn die Kurzform etwa {2,0,8} x {1,0,0}(4)lautet, enthält der Knoten zwei periodische Strukturen.
NODE DESCRIPTION: Zeigt die Langform der Formel an, die dem Format der Formel in der Mininglegendeentspricht. Die Langform entspricht der Kurzform, mit dem Unterschied, dass die Istwerte der Koeffizienten angezeigt werden.
NODE_RULE: zeigt eine XML-Darstellung der Formel an. Abhängig vom Knotentyp kann die XML-Darstellung einzelne oder mehrere periodische Strukturen enthalten. Die folgende Tabelle zeigt, wie ein Rollup der XML-Knoten auf höhere Ebenen des ARIMA-Modells durchgeführt wird.
| Knotentyp | XML-Inhalt |
|---|---|
| 27 (ARIMA-Stamm) | Enthält alle periodischen Strukturen für die Datenreihe und den Inhalt aller untergeordneten Knoten für die einzelnen periodischen Strukturen. |
| 28 (ARIMA Periodische Struktur) | Definiert eine einzelne periodische Struktur, einschließlich des Knotens für die autoregressive Reihenfolge und der Koeffizienten für den gleitenden Durchschnitt. |
| 29 (ARIMA Autoregressiv) | Listet die Ausdrücke für eine einzelne periodische Struktur auf. |
| 30 (ARIMA Gleitender Durchschnitt) | Listet die Koeffizienten für eine einzelne periodische Struktur auf. |
NODE_DISTRIBUTION: zeigt die Ausdrücke der Formel in einer geschachtelten Tabelle an, die Sie nach bestimmten Ausdrücken abfragen können. Die NODE_DISTRIBUTION-Tabelle weist dieselbe hierarchische Struktur auf wie die XML-Regeln. Das heißt, der Stammknoten der ARIMA-Reihe (NODE_TYPE = 27) enthält den Wert des konstanten Glieds und der Periodizitäten für die gesamte Formel, wobei es sich um mehrere Periodizitäten handeln kann, und die untergeordneten Knoten enthalten lediglich spezifische Informationen zu einer bestimmten periodischen Struktur bzw. die untergeordneten Knoten dieser periodischen Struktur.
| Knotentyp | attribute | Werttyp |
|---|---|---|
| 27 (ARIMA-Stamm) | Konstantes Glied Periodizität |
11 |
| 28 (ARIMA Periodische Struktur) | Periodizität Autoregressive Reihenfolge Differenzreihenfolge Reihenfolge für gleitenden Durchschnitt |
12 13 15 14 |
| 29 (ARIMA Autoregressiv) | Koeffizient (Komplement des Koeffizienten) |
7 |
| 30 (ARIMA Gleitender Durchschnitt) | Wert bei "t" Wert bei "t-1" ... Wert bei "t-n" |
7 |
Der Wert für die Reihenfolge für gleitenden Durchschnitt gibt die Anzahl der gleitenden Durchschnittswerte in einer Reihe an. In der Regel wird der gleitende Durchschnitt n-1 Mal berechnet, wenn n Ausdrücke in einer Reihe enthalten sind, die Zahl kann jedoch zur Vereinfachung des Prozesses reduziert werden.
Der Wert für autoregressive Reihenfolge gibt die Anzahl der autoregressiven Reihen an.
Der Wert für Differenzreihenfolge gibt an, wie viele Male die Reihen verglichen bzw. differenziert werden.
Eine Enumeration der möglichen Werttypen finden Sie unter Microsoft.AnalysisServices.AdomdServer.MiningValueType.
Verwenden der ARIMA-Strukturinformationen
Wenn Sie in einer Geschäftslösung Vorhersagen verwenden, die auf dem ARIMA-Algorithmus basieren, sollten Sie die Formel in ein Dokument einfügen, um zu veranschaulichen, mit welcher Methode die Vorhersage erstellt wurde. Sie können die Beschriftung oder die Beschreibung verwenden, um die Formeln in Kurzform bzw. in Langform darzustellen.
Wenn Sie eine Anwendung entwickeln, die Zeitreihenvorhersagen verwendet, empfiehlt es sich, die ARIMA-Formel aus dem Modellinhalt abzurufen und dann eigene Vorhersagen zu erstellen. Zum Abrufen der ARIMA-Formel für eine bestimmte Ausgabe können Sie im ARIMA-Stamm eine direkte Abfrage nach dem Attribut ausführen, wie in den vorherigen Beispielen gezeigt.
Wenn Sie die ID des Knotens kennen, der die gewünschte Reihe enthält, haben Sie zwei Möglichkeiten zum Abrufen der Formelkomponenten:
Geschachtelte Tabelle: DMX-Abfrage oder Abfrage über OLEDB-Client
XML-Darstellung: XML-Abfrage
Hinweise
Die Abfrage von Informationen aus einer ARTXP-Struktur kann kompliziert sein, da sich die Informationen für jede Teilung innerhalb der Struktur an einer anderen Position befinden. Wenn Sie mit einem ARTXP-Modell arbeiten, müssen Sie aus diesem Grund alle Teile abrufen und dann einige Verarbeitungsvorgänge ausführen, um die vollständige Formel wieder zusammenzusetzen. Das Abrufen einer Formel aus einem ARIMA-Modell ist einfacher, da die Formel strukturweit verfügbar gemacht wird. Informationen zum Erstellen einer Abfrage zum Abrufen dieser Informationen finden Sie unter Abfragebeispiel Zeitreihenmodell.
Weitere Informationen
Miningmodellinhalt (Analysis Services –</ph> Data Mining)
Microsoft Time Series-Algorithmus
Abfragebeispiel Zeitreihenmodell
Microsoft Time Series Algorithm Technical Reference