System.Drawing.Drawing2D.Matrix-Klasse
Dieser Artikel enthält ergänzende Hinweise zur Referenzdokumentation für diese API.
Die Matrix Klasse kapselt eine 3:3-affine Matrix, die eine geometrische Transformation darstellt.
In GDI+ können Sie eine affine Transformation in einem Matrix Objekt speichern. Da die dritte Spalte einer Matrix, die eine affine Transformation darstellt, immer (0, 0, 1) ist, geben Sie nur die sechs Zahlen in den ersten beiden Spalten an, wenn Sie ein Matrix-Objekt erstellen. Die Anweisung Matrix myMatrix = new Matrix(0, 1, -1, 0, 3, 4) erstellt die matrix, die in der folgenden Abbildung dargestellt ist.
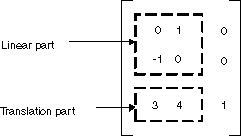
Hinweis
In .NET 6 und höheren Versionen wird das System.Drawing.Common-Paket, das diesen Typ enthält, nur unter Windows-Betriebssystemen unterstützt. Die Verwendung dieses Typs in plattformübergreifenden Apps führt zu Kompilierungszeitwarnungen und Laufzeit-Ausnahmen. Weitere Informationen finden Sie unter "System.Drawing.Common", das nur unter Windows unterstützt wird.
Zusammengesetzte Transformationen
Eine zusammengesetzte Transformation ist eine Sequenz von Transformationen (eine nach der anderen). Sehen Sie sich die Matrizen und Transformationen in der folgenden Liste an:
| Matrix | Transformation |
|---|---|
| Matrix A | Um 90 Grad drehen |
| Matrix B | Um den Faktor 2 in x-Richtung skalieren |
| Matrix C | Drei Einheiten in y-Richtung verschieben |
Wenn Sie mit dem Punkt (2, 1) beginnen - dargestellt durch die Matrix [2 1 1] - und multiplizieren sie mit A, dann B, dann C, der Punkt (2, 1) wird den drei Transformationen in der aufgeführten Reihenfolge unterzogen.
[2 1 1]ABC = [-2 5 1]
Anstatt die drei Teile der zusammengesetzten Transformation in drei separaten Matrizen zu speichern, können Sie A, B und C gemeinsam multiplizieren, um eine einzelne 3×3-Matrix zu erhalten, die die gesamte zusammengesetzte Transformation speichert. Gehen Sie vom Wert ABC = D aus. Dann gibt ein mit D multiplizierter Punkt dasselbe Ergebnis wie ein mit A multiplizierter Punkt, dann B und dann C.
[2 1 1]D = [-2 5 1]
Die folgende Abbildung zeigt die Matrizen A, B, C und D:
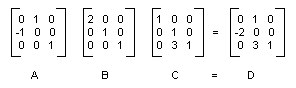
Die Tatsache, dass die Matrix einer zusammengesetzten Transformation durch Multiplizieren der einzelnen Transformationsmatrizen gebildet werden kann, bedeutet, dass jede Sequenz affiner Transformationen in einem einzelnen Matrix-Objekt gespeichert werden kann.
Achtung
Die Reihenfolge einer zusammengesetzten Transformation ist wichtig. Im Allgemeinen ist Drehen > Skalieren > Verschieben nicht das Gleiche wie Skalieren > Drehen > Verschieben. Auch die Reihenfolge der Matrixmultiplikation ist wichtig. ABC ist im Allgemeinen nicht das Gleiche wie BAC.
Die Klasse Matrix bietet mehrere Methoden zur Erstellung einer zusammengesetzten Transformation: Multiply, Rotate, RotateAt, Scale, Shear und Translate. Im folgenden Beispiel wird die Matrix einer zusammengesetzten Transformation erstellt. Dabei wird zuerst eine 30-Grad-Drehung durchgeführt. Danach folgen eine Skalierung um den Faktor 2 in y-Richtung und eine Verschiebung um fünf Einheiten in x-Richtung:
Matrix myMatrix = new Matrix();
myMatrix.Rotate(30);
myMatrix.Scale(1, 2, MatrixOrder.Append);
myMatrix.Translate(5, 0, MatrixOrder.Append);
Dim myMatrix As New Matrix()
myMatrix.Rotate(30)
myMatrix.Scale(1, 2, MatrixOrder.Append)
myMatrix.Translate(5, 0, MatrixOrder.Append)
