Math Behind the Hashing Birthday Attack
Last time I was looking at hashing algorithms when I pointed out that finding collisions was easier than reversing a message digest. For a good hashing algorithm, finding a message with a particular digest generally requires looking at as many messages as the size of the message digest space. If you have a 64-bit message digest, then you need to look at 2^64 messages, more or less (a little less actually).
It turns out that it takes looking at far fewer messages on average to find a collision. The cause of this is something called the birthday paradox. The birthday paradox comes from the question whether any two people in a crowded room were born on the same day of the year. Most people guess that everyone has a unique birthday unless there's at least a hundred people in the room. In reality, it turns out that it only takes about two dozen people before it's more likely than not that two share a common birthday. Here's why.
Take M to be the size of the message digest space, say 2^64 or so. Then, the probability that there's a collision in a group of N messages is one minus the chance of every message having a unique message digest.
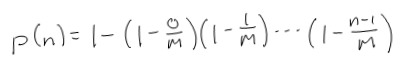
Now, this is an inconvenient thing to try to solve for particular values of M and N. What we can do is take an approximation to that product to make it easier to evaluate.

I've used an expansion of e^x to first convert the terms of the product and then collapse all of the terms together into a simple expression. We still need to solve for N though to find out how difficult it is to come up with collisions.

I put 0.5 in as the probability I was looking for, and then found an expression for N in terms of a constant times the square root of M. This shows that you only have to look at slightly more than 2^32 messages to find a collision for a 64-bit message digest. On the other hand, you need to look at slightly less than 2^64 messages to reverse a particular message digest. This is why collisions are so much harder to protect against than reversibility.
Next time: Using the BufferManager
Comments
- Anonymous
May 19, 2006
In the Basics of Transport Security article I wrote a few weeks ago, I introduced three different kinds... - Anonymous
July 21, 2006
Nicholas Allen has some excellent posts about WCF where he gets into a lot of the nitty-gritty and explains... - Anonymous
July 28, 2006
When using symmetric encryption, repetition is the enemy of security. For the basic stream cipher and... - Anonymous
October 17, 2006
When using symmetric encryption, repetition is the enemy of security. For the basic stream cipher and