Exercise - Estimate resources for a real-world problem
Shor's factoring algorithm is one of the most well-known quantum algorithms. It offers an exponential speedup over any known classical factoring algorithm.
Classic cryptography uses physical or mathematical means, like computational difficulty, to accomplish a task. A popular cryptographic protocol is the Rivest–Shamir–Adleman (RSA) scheme, which is based on the assumption of the difficulty of factoring prime numbers by using a classical computer.
The Shor's algorithm implies that sufficiently large quantum computers can break public-key cryptography. Estimating the resources required for Shor’s algorithm is important to assess the vulnerability of these types of cryptographic schemes.
In the following exercise, you'll calculate the resource estimates for the factoring of a 2,048-bit integer. For this application, you'll compute the physical resource estimates directly from precomputed logical resource estimates. For the tolerated error budget, you'll use $\epsilon = 1/3$.
Write the Shor's algorithm
In Visual Studio Code, select View > Command palette and select Create: New Jupyter Notebook.
Save the notebook as ShorRE.ipynb.
In the first cell, import the
qsharppackage:import qsharpUse the
Microsoft.Quantum.ResourceEstimationnamespace to define a cached, optimized version of Shor's integer factorization algorithm. Add a new cell and copy and paste the following code:%%qsharp open Microsoft.Quantum.Arrays; open Microsoft.Quantum.Canon; open Microsoft.Quantum.Convert; open Microsoft.Quantum.Diagnostics; open Microsoft.Quantum.Intrinsic; open Microsoft.Quantum.Math; open Microsoft.Quantum.Measurement; open Microsoft.Quantum.Unstable.Arithmetic; open Microsoft.Quantum.ResourceEstimation; operation RunProgram() : Unit { let bitsize = 31; // When choosing parameters for `EstimateFrequency`, make sure that // generator and modules are not co-prime let _ = EstimateFrequency(11, 2^bitsize - 1, bitsize); } // In this sample we concentrate on costing the `EstimateFrequency` // operation, which is the core quantum operation in Shors algorithm, and // we omit the classical pre- and post-processing. /// # Summary /// Estimates the frequency of a generator /// in the residue ring Z mod `modulus`. /// /// # Input /// ## generator /// The unsigned integer multiplicative order (period) /// of which is being estimated. Must be co-prime to `modulus`. /// ## modulus /// The modulus which defines the residue ring Z mod `modulus` /// in which the multiplicative order of `generator` is being estimated. /// ## bitsize /// Number of bits needed to represent the modulus. /// /// # Output /// The numerator k of dyadic fraction k/2^bitsPrecision /// approximating s/r. operation EstimateFrequency( generator : Int, modulus : Int, bitsize : Int ) : Int { mutable frequencyEstimate = 0; let bitsPrecision = 2 * bitsize + 1; // Allocate qubits for the superposition of eigenstates of // the oracle that is used in period finding. use eigenstateRegister = Qubit[bitsize]; // Initialize eigenstateRegister to 1, which is a superposition of // the eigenstates we are estimating the phases of. // We first interpret the register as encoding an unsigned integer // in little endian encoding. ApplyXorInPlace(1, eigenstateRegister); let oracle = ApplyOrderFindingOracle(generator, modulus, _, _); // Use phase estimation with a semiclassical Fourier transform to // estimate the frequency. use c = Qubit(); for idx in bitsPrecision - 1..-1..0 { within { H(c); } apply { // `BeginEstimateCaching` and `EndEstimateCaching` are the operations // exposed by Azure Quantum Resource Estimator. These will instruct // resource counting such that the if-block will be executed // only once, its resources will be cached, and appended in // every other iteration. if BeginEstimateCaching("ControlledOracle", SingleVariant()) { Controlled oracle([c], (1 <<< idx, eigenstateRegister)); EndEstimateCaching(); } R1Frac(frequencyEstimate, bitsPrecision - 1 - idx, c); } if MResetZ(c) == One { set frequencyEstimate += 1 <<< (bitsPrecision - 1 - idx); } } // Return all the qubits used for oracles eigenstate back to 0 state // using Microsoft.Quantum.Intrinsic.ResetAll. ResetAll(eigenstateRegister); return frequencyEstimate; } /// # Summary /// Interprets `target` as encoding unsigned little-endian integer k /// and performs transformation |k⟩ ↦ |gᵖ⋅k mod N ⟩ where /// p is `power`, g is `generator` and N is `modulus`. /// /// # Input /// ## generator /// The unsigned integer multiplicative order ( period ) /// of which is being estimated. Must be co-prime to `modulus`. /// ## modulus /// The modulus which defines the residue ring Z mod `modulus` /// in which the multiplicative order of `generator` is being estimated. /// ## power /// Power of `generator` by which `target` is multiplied. /// ## target /// Register interpreted as LittleEndian which is multiplied by /// given power of the generator. The multiplication is performed modulo /// `modulus`. internal operation ApplyOrderFindingOracle( generator : Int, modulus : Int, power : Int, target : Qubit[] ) : Unit is Adj + Ctl { // The oracle we use for order finding implements |x⟩ ↦ |x⋅a mod N⟩. We // also use `ExpModI` to compute a by which x must be multiplied. Also // note that we interpret target as unsigned integer in little-endian // encoding by using the `LittleEndian` type. ModularMultiplyByConstant(modulus, ExpModI(generator, power, modulus), target); } /// # Summary /// Performs modular in-place multiplication by a classical constant. /// /// # Description /// Given the classical constants `c` and `modulus`, and an input /// quantum register (as LittleEndian) |𝑦⟩, this operation /// computes `(c*x) % modulus` into |𝑦⟩. /// /// # Input /// ## modulus /// Modulus to use for modular multiplication /// ## c /// Constant by which to multiply |𝑦⟩ /// ## y /// Quantum register of target internal operation ModularMultiplyByConstant(modulus : Int, c : Int, y : Qubit[]) : Unit is Adj + Ctl { use qs = Qubit[Length(y)]; for (idx, yq) in Enumerated(y) { let shiftedC = (c <<< idx) % modulus; Controlled ModularAddConstant([yq], (modulus, shiftedC, qs)); } ApplyToEachCA(SWAP, Zipped(y, qs)); let invC = InverseModI(c, modulus); for (idx, yq) in Enumerated(y) { let shiftedC = (invC <<< idx) % modulus; Controlled ModularAddConstant([yq], (modulus, modulus - shiftedC, qs)); } } /// # Summary /// Performs modular in-place addition of a classical constant into a /// quantum register. /// /// # Description /// Given the classical constants `c` and `modulus`, and an input /// quantum register (as LittleEndian) |𝑦⟩, this operation /// computes `(x+c) % modulus` into |𝑦⟩. /// /// # Input /// ## modulus /// Modulus to use for modular addition /// ## c /// Constant to add to |𝑦⟩ /// ## y /// Quantum register of target internal operation ModularAddConstant(modulus : Int, c : Int, y : Qubit[]) : Unit is Adj + Ctl { body (...) { Controlled ModularAddConstant([], (modulus, c, y)); } controlled (ctrls, ...) { // We apply a custom strategy to control this operation instead of // letting the compiler create the controlled variant for us in which // the `Controlled` functor would be distributed over each operation // in the body. // // Here we can use some scratch memory to save ensure that at most one // control qubit is used for costly operations such as `AddConstant` // and `CompareGreaterThenOrEqualConstant`. if Length(ctrls) >= 2 { use control = Qubit(); within { Controlled X(ctrls, control); } apply { Controlled ModularAddConstant([control], (modulus, c, y)); } } else { use carry = Qubit(); Controlled AddConstant(ctrls, (c, y + [carry])); Controlled Adjoint AddConstant(ctrls, (modulus, y + [carry])); Controlled AddConstant([carry], (modulus, y)); Controlled CompareGreaterThanOrEqualConstant(ctrls, (c, y, carry)); } } } /// # Summary /// Performs in-place addition of a constant into a quantum register. /// /// # Description /// Given a non-empty quantum register |𝑦⟩ of length 𝑛+1 and a positive /// constant 𝑐 < 2ⁿ, computes |𝑦 + c⟩ into |𝑦⟩. /// /// # Input /// ## c /// Constant number to add to |𝑦⟩. /// ## y /// Quantum register of second summand and target; must not be empty. internal operation AddConstant(c : Int, y : Qubit[]) : Unit is Adj + Ctl { // We are using this version instead of the library version that is based // on Fourier angles to show an advantage of sparse simulation in this sample. let n = Length(y); Fact(n > 0, "Bit width must be at least 1"); Fact(c >= 0, "constant must not be negative"); Fact(c < 2 ^ n, $"constant must be smaller than {2L ^ n}"); if c != 0 { // If c has j trailing zeroes than the j least significant bits // of y will not be affected by the addition and can therefore be // ignored by applying the addition only to the other qubits and // shifting c accordingly. let j = NTrailingZeroes(c); use x = Qubit[n - j]; within { ApplyXorInPlace(c >>> j, x); } apply { IncByLE(x, y[j...]); } } } /// # Summary /// Performs greater-than-or-equals comparison to a constant. /// /// # Description /// Toggles output qubit `target` if and only if input register `x` /// is greater than or equal to `c`. /// /// # Input /// ## c /// Constant value for comparison. /// ## x /// Quantum register to compare against. /// ## target /// Target qubit for comparison result. /// /// # Reference /// This construction is described in [Lemma 3, arXiv:2201.10200] internal operation CompareGreaterThanOrEqualConstant(c : Int, x : Qubit[], target : Qubit) : Unit is Adj+Ctl { let bitWidth = Length(x); if c == 0 { X(target); } elif c >= 2 ^ bitWidth { // do nothing } elif c == 2 ^ (bitWidth - 1) { ApplyLowTCNOT(Tail(x), target); } else { // normalize constant let l = NTrailingZeroes(c); let cNormalized = c >>> l; let xNormalized = x[l...]; let bitWidthNormalized = Length(xNormalized); let gates = Rest(IntAsBoolArray(cNormalized, bitWidthNormalized)); use qs = Qubit[bitWidthNormalized - 1]; let cs1 = [Head(xNormalized)] + Most(qs); let cs2 = Rest(xNormalized); within { for i in IndexRange(gates) { (gates[i] ? ApplyAnd | ApplyOr)(cs1[i], cs2[i], qs[i]); } } apply { ApplyLowTCNOT(Tail(qs), target); } } } /// # Summary /// Internal operation used in the implementation of GreaterThanOrEqualConstant. internal operation ApplyOr(control1 : Qubit, control2 : Qubit, target : Qubit) : Unit is Adj { within { ApplyToEachA(X, [control1, control2]); } apply { ApplyAnd(control1, control2, target); X(target); } } internal operation ApplyAnd(control1 : Qubit, control2 : Qubit, target : Qubit) : Unit is Adj { body (...) { CCNOT(control1, control2, target); } adjoint (...) { H(target); if (M(target) == One) { X(target); CZ(control1, control2); } } } /// # Summary /// Returns the number of trailing zeroes of a number /// /// ## Example /// ```qsharp /// let zeroes = NTrailingZeroes(21); // = NTrailingZeroes(0b1101) = 0 /// let zeroes = NTrailingZeroes(20); // = NTrailingZeroes(0b1100) = 2 /// ``` internal function NTrailingZeroes(number : Int) : Int { mutable nZeroes = 0; mutable copy = number; while (copy % 2 == 0) { set nZeroes += 1; set copy /= 2; } return nZeroes; } /// # Summary /// An implementation for `CNOT` that when controlled using a single control uses /// a helper qubit and uses `ApplyAnd` to reduce the T-count to 4 instead of 7. internal operation ApplyLowTCNOT(a : Qubit, b : Qubit) : Unit is Adj+Ctl { body (...) { CNOT(a, b); } adjoint self; controlled (ctls, ...) { // In this application this operation is used in a way that // it is controlled by at most one qubit. Fact(Length(ctls) <= 1, "At most one control line allowed"); if IsEmpty(ctls) { CNOT(a, b); } else { use q = Qubit(); within { ApplyAnd(Head(ctls), a, q); } apply { CNOT(q, b); } } } controlled adjoint self; }
Estimate the Shor's algorithm
Now, estimate the physical resources for the RunProgram operation using the default assumptions. Add a new cell and copy and paste the following code:
result = qsharp.estimate("RunProgram()")
result
The qsharp.estimate function creates a result object you can use to display a table with the overall physical resource counts. You can inspect cost details by collapsing the groups, which have more information.
For example, collapse the Logical qubit parameters group to see that the code distance is 21 and the number of physical qubits is 882.
| Logical qubit parameter | Value |
|---|---|
| QEC scheme | surface_code |
| Code distance | 21 |
| Physical qubits | 882 |
| Logical cycle time | 8 milisecs |
| Logical qubit error rate | 3.00E-13 |
| Crossing prefactor | 0.03 |
| Error correction threshold | 0.01 |
| Logical cycle time formula | (4 * twoQubitGateTime + 2 * oneQubitMeasurementTime) * codeDistance |
| Physical qubits formula | 2 * codeDistance * codeDistance |
Tip
For a more compact version of the output table, you can use result.summary.
Space diagram
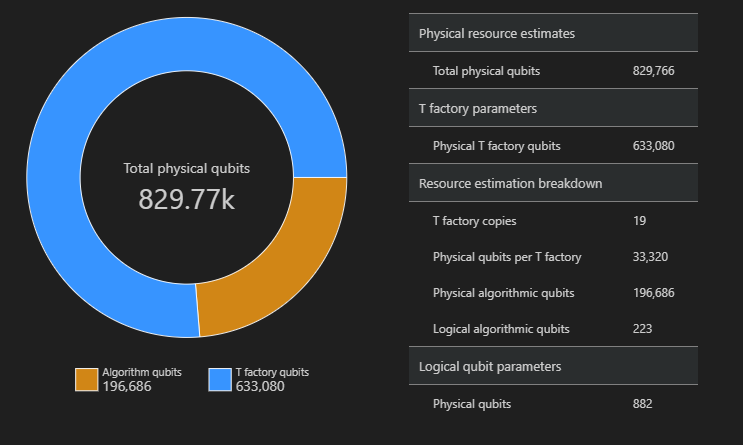
The distribution of physical qubits used for the algorithm and the T factories is a factor which might impact your algorithm's design. You can use the qsharp-widgets package to visualize this distribution to better understand the algorithm's estimated space requirements.
from qsharp_widgets import SpaceChart
SpaceChart(result)
In this example, the number of physical qubits required to run the algorithm is 829766, 196686 of which are algorithm qubits and 633080 of which are T factory qubits.
Compare the resource estimates for different qubit technologies
The Azure Quantum Resource Estimator allows you to run multiple configurations of target parameters and compare the results. This is useful when you want to compare the cost of different qubit models, QEC schemes, or error budgets.
You can also construct a list of estimation parameters using the EstimatorParams object.
from qsharp.estimator import EstimatorParams, QubitParams, QECScheme, LogicalCounts
labels = ["Gate-based µs, 10⁻³", "Gate-based µs, 10⁻⁴", "Gate-based ns, 10⁻³", "Gate-based ns, 10⁻⁴", "Majorana ns, 10⁻⁴", "Majorana ns, 10⁻⁶"]
params = EstimatorParams(6)
params.error_budget = 0.333
params.items[0].qubit_params.name = QubitParams.GATE_US_E3
params.items[1].qubit_params.name = QubitParams.GATE_US_E4
params.items[2].qubit_params.name = QubitParams.GATE_NS_E3
params.items[3].qubit_params.name = QubitParams.GATE_NS_E4
params.items[4].qubit_params.name = QubitParams.MAJ_NS_E4
params.items[4].qec_scheme.name = QECScheme.FLOQUET_CODE
params.items[5].qubit_params.name = QubitParams.MAJ_NS_E6
params.items[5].qec_scheme.name = QECScheme.FLOQUET_CODE
qsharp.estimate("RunProgram()", params=params).summary_data_frame(labels=labels)
| Qubit model | Logical qubits | Logical depth | T states | Code distance | T factories | T factory fraction | Physical qubits | rQOPS | Physical runtime |
|---|---|---|---|---|---|---|---|---|---|
| Gate-based µs, 10⁻³ | 223 3.64M | 4.70M | 17 | 13 | 40.54 % | 216.77k | 21.86k | 10 hours | |
| Gate-based µs, 10⁻⁴ | 223 | 3.64M | 4.70M | 9 | 14 | 43.17 % | 63.57k | 41.30k | 5 hours |
| Gate-based ns, 10⁻³ | 223 3.64M | 4.70M | 17 | 16 | 69.08 % | 416.89k | 32.79M | 25 secs | |
| Gate-based ns, 10⁻⁴ | 223 3.64M | 4.70M | 9 | 14 | 43.17 % | 63.57k | 61.94M | 13 secs | |
| Majorana ns, 10⁻⁴ | 223 3.64M | 4.70M | 9 | 19 | 82.75 % | 501.48k | 82.59M | 10 secs | |
| Majorana ns, 10⁻⁶ | 223 3.64M | 4.70M | 5 | 13 | 31.47 % | 42.96k | 148.67M | 5 secs |
Extract resource estimates from logical resource counts
If you already know some estimates for an operation, the Resource Estimator allows you to incorporate the known estimates into the overall program cost to reduce the execution time. You can use the LogicalCounts class to extract the logical resource estimates from precalculated resource estimation values.
Select Code to add a new cell, and then enter and run the following code:
logical_counts = LogicalCounts({
'numQubits': 12581,
'tCount': 12,
'rotationCount': 12,
'rotationDepth': 12,
'cczCount': 3731607428,
'measurementCount': 1078154040})
logical_counts.estimate(params).summary_data_frame(labels=labels)
| Qubit model | Logical qubits | Logical depth | T states | Code distance | T factories | T factory fraction | Physical qubits | Physical runtime |
|---|---|---|---|---|---|---|---|---|
| Gate-based µs, 10⁻³ | 25481 | 1.2e+10 | 1.5e+10 | 27 | 13 | 0.6% | 37.38M | 6 years |
| Gate-based µs, 10⁻⁴ | 25481 | 1.2e+10 | 1.5e+10 | 13 | 14 | 0.8% | 8.68M | 3 years |
| Gate-based ns, 10⁻³ | 25481 | 1.2e+10 | 1.5e+10 | 27 | 15 | 1.3% | 37.65M | 2 days |
| Gate-based ns, 10⁻⁴ | 25481 | 1.2e+10 | 1.5e+10 | 13 | 18 | 1.2% | 8.72M | 18 hours |
| Majorana ns, 10⁻⁴ | 25481 | 1.2e+10 | 1.5e+10 | 15 | 15 | 1.3% | 26.11M | 15 hours |
| Majorana ns, 10⁻⁶ | 25481 | 1.2e+10 | 1.5e+10 | 7 | 13 | 0.5% | 6.25M | 7 hours |
Conclusion
In the worst scenario, a quantum computer using gate-based µs qubits (qubits that have operation times in the nanosecond regime, such as superconducting qubits) and a surface QEC code would need six years and 37.38 millions of qubits to factor a 2,048-bit integer by using Shor's algorithm.
If you use a different qubit technology—for example, gate-based ns ion qubits—and the same surface code, the number of qubits doesn't change much, but the runtime becomes two days in the worst case and 18 hours in the optimistic case. If you change the qubit technology and the QEC code—for example, by using Majorana-based qubits—factoring a 2,048-bit integer by using Shor’s algorithm could be done in hours with an array of 6.25 millions of qubits in the best-case scenario.
From your experiment, you can conclude that using Majorana qubits and a Floquet QEC code is the best choice to execute Shor's algorithm and factor a 2,048-bit integer.