Uses and applications of quantum computing
In this unit, you explore some of the most promising applications of quantum computing.
What problems can quantum computers solve?
A quantum computer isn't a supercomputer that can do everything faster or that can solve any possible problem. A quantum computer expands the set of problems that we can solve efficiently, but there still exist problems that are too complex for a quantum computer to solve.
The following diagram shows the different sets of problems by their complexity. The problems that a quantum computer can solve more efficiently than a classical computer are called BQP (bounded-error quantum polynomials). The name means that they're solvable by a quantum computer in polynomial time. Examples of BQP problems include the factoring problem and the search problem.
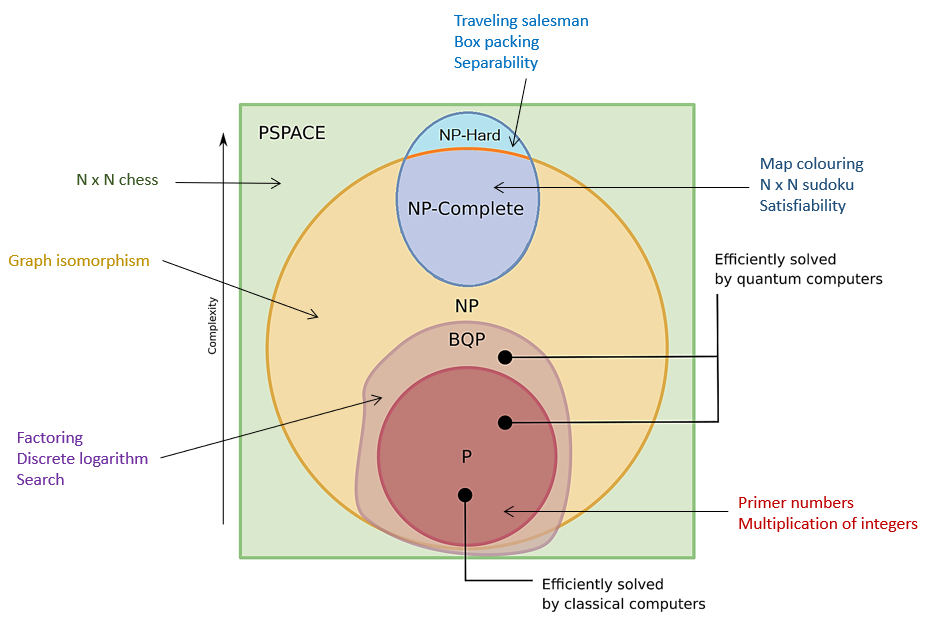
In fact, one of the goals of quantum computing research is to study which problems a quantum computer can solve faster than a classical computer, and how large the speedup can be. Quantum computers do exceptionally well with problems that require calculating a large number of possible combinations.
Quantum simulation
Quantum mechanics is the underlying "operating system" of our universe. It describes how the fundamental building blocks of nature behave. Nature's behaviors, such as chemical reactions, biological reactions, and material formations, often involve many-body quantum interactions. Quantum computing is promising for simulating intrinsically quantum mechanical systems, such as molecules, because qubits can be used to represent the natural states in question. Examples of quantum systems that we can model include photosynthesis, superconductivity, and complex molecular formations.
Resource estimation
The Azure Quantum Azure Resource Estimator helps you prepare for the future of quantum computing by providing a way to estimate the resources required to run your quantum programs on scaled quantum computers. It helps you answer questions such as what hardware resources are required? How many physical and logical qubits are needed and what type? How long is the run time?
As a result, you're able to refine your algorithms and build solutions that take advantage of scaled quantum computers when they become available.
Quantum speedups
One of the goals of quantum computing research is to study which problems a quantum computer can solve faster than a classical computer, and how large the speedup can be. Two well-known examples are Grover's algorithm and Shor's algorithm, which yield a polynomial and an exponential speedup, respectively, over their classical counterparts.
Shor's algorithm running on a quantum computer could break classical cryptographic schemes such as the Rivest–Shamir–Adleman (RSA) scheme, which is widely used in e-commerce for secure data transmission. This scheme is based on the practical difficulty of factoring prime numbers by using classical algorithms.
Grover's algorithm speeds up the solution to unstructured data searches, running the search in fewer steps than any classical algorithm could. Indeed, any problem that allows you to check whether a given value is a valid solution (a "yes or no" problem) can be formulated in terms of the search problem.