Diferentes formas de ejecutar el estimador de recursos
En este artículo, aprenderá a trabajar con el estimador de recursos de Azure Quantum. El estimador de recursos le ayuda a calcular los recursos necesarios para ejecutar un programa cuántico en un equipo cuántico. Puede usar el estimador de recursos para calcular el número de cúbits, el número de puertas y la profundidad del circuito necesario para ejecutar un programa cuántico.
El estimador de recursos está disponible en Visual Studio Code con la extensión Quantum Development Kit. Para obtener más información, consulte Instalación del Kit de Desarrollo Cuántico.
Advertencia
El estimador de recursos de Azure Portal está en desuso. Recomendamos que realice la transición al Estimador de Recursos local en Visual Studio Code proporcionado en el Quantum Development Kit .
Requisitos previos para VS Code
- La versión más reciente de Visual Studio Code o abrir VS Code en la Web.
- La versión más reciente de Extensión de kit de desarrollo de Quantum. Para obtener más información sobre la instalación, consulte Instalación del QDK en VS Code.
Sugerencia
No es necesario tener una cuenta de Azure para ejecutar el estimador de recursos.
Creación de un nuevo archivo Q#
- Abra Visual Studio Code y seleccione Archivo > Nuevo archivo de texto para crear un nuevo archivo.
- Guarde el archivo como
ShorRE.qs. Este archivo contendrá el código Q# del programa.
Creación del algoritmo cuántico
Copie el código siguiente en el archivo ShorRE.qs:
import Std.Arrays.*;
import Std.Canon.*;
import Std.Convert.*;
import Std.Diagnostics.*;
import Std.Math.*;
import Std.Measurement.*;
import Microsoft.Quantum.Unstable.Arithmetic.*;
import Std.ResourceEstimation.*;
operation Main() : Unit {
let bitsize = 31;
// When choosing parameters for `EstimateFrequency`, make sure that
// generator and modules are not co-prime
let _ = EstimateFrequency(11, 2^bitsize - 1, bitsize);
}
// In this sample we concentrate on costing the `EstimateFrequency`
// operation, which is the core quantum operation in Shors algorithm, and
// we omit the classical pre- and post-processing.
/// # Summary
/// Estimates the frequency of a generator
/// in the residue ring Z mod `modulus`.
///
/// # Input
/// ## generator
/// The unsigned integer multiplicative order (period)
/// of which is being estimated. Must be co-prime to `modulus`.
/// ## modulus
/// The modulus which defines the residue ring Z mod `modulus`
/// in which the multiplicative order of `generator` is being estimated.
/// ## bitsize
/// Number of bits needed to represent the modulus.
///
/// # Output
/// The numerator k of dyadic fraction k/2^bitsPrecision
/// approximating s/r.
operation EstimateFrequency(
generator : Int,
modulus : Int,
bitsize : Int
)
: Int {
mutable frequencyEstimate = 0;
let bitsPrecision = 2 * bitsize + 1;
// Allocate qubits for the superposition of eigenstates of
// the oracle that is used in period finding.
use eigenstateRegister = Qubit[bitsize];
// Initialize eigenstateRegister to 1, which is a superposition of
// the eigenstates we are estimating the phases of.
// We first interpret the register as encoding an unsigned integer
// in little endian encoding.
ApplyXorInPlace(1, eigenstateRegister);
let oracle = ApplyOrderFindingOracle(generator, modulus, _, _);
// Use phase estimation with a semiclassical Fourier transform to
// estimate the frequency.
use c = Qubit();
for idx in bitsPrecision - 1..-1..0 {
within {
H(c);
} apply {
// `BeginEstimateCaching` and `EndEstimateCaching` are the operations
// exposed by Azure Quantum Resource Estimator. These will instruct
// resource counting such that the if-block will be executed
// only once, its resources will be cached, and appended in
// every other iteration.
if BeginEstimateCaching("ControlledOracle", SingleVariant()) {
Controlled oracle([c], (1 <<< idx, eigenstateRegister));
EndEstimateCaching();
}
R1Frac(frequencyEstimate, bitsPrecision - 1 - idx, c);
}
if MResetZ(c) == One {
frequencyEstimate += 1 <<< (bitsPrecision - 1 - idx);
}
}
// Return all the qubits used for oracles eigenstate back to 0 state
// using Microsoft.Quantum.Intrinsic.ResetAll.
ResetAll(eigenstateRegister);
return frequencyEstimate;
}
/// # Summary
/// Interprets `target` as encoding unsigned little-endian integer k
/// and performs transformation |k⟩ ↦ |gᵖ⋅k mod N ⟩ where
/// p is `power`, g is `generator` and N is `modulus`.
///
/// # Input
/// ## generator
/// The unsigned integer multiplicative order ( period )
/// of which is being estimated. Must be co-prime to `modulus`.
/// ## modulus
/// The modulus which defines the residue ring Z mod `modulus`
/// in which the multiplicative order of `generator` is being estimated.
/// ## power
/// Power of `generator` by which `target` is multiplied.
/// ## target
/// Register interpreted as little endian encoded which is multiplied by
/// given power of the generator. The multiplication is performed modulo
/// `modulus`.
internal operation ApplyOrderFindingOracle(
generator : Int, modulus : Int, power : Int, target : Qubit[]
)
: Unit
is Adj + Ctl {
// The oracle we use for order finding implements |x⟩ ↦ |x⋅a mod N⟩. We
// also use `ExpModI` to compute a by which x must be multiplied. Also
// note that we interpret target as unsigned integer in little-endian
// encoding.
ModularMultiplyByConstant(modulus,
ExpModI(generator, power, modulus),
target);
}
/// # Summary
/// Performs modular in-place multiplication by a classical constant.
///
/// # Description
/// Given the classical constants `c` and `modulus`, and an input
/// quantum register |𝑦⟩, this operation
/// computes `(c*x) % modulus` into |𝑦⟩.
///
/// # Input
/// ## modulus
/// Modulus to use for modular multiplication
/// ## c
/// Constant by which to multiply |𝑦⟩
/// ## y
/// Quantum register of target
internal operation ModularMultiplyByConstant(modulus : Int, c : Int, y : Qubit[])
: Unit is Adj + Ctl {
use qs = Qubit[Length(y)];
for (idx, yq) in Enumerated(y) {
let shiftedC = (c <<< idx) % modulus;
Controlled ModularAddConstant([yq], (modulus, shiftedC, qs));
}
ApplyToEachCA(SWAP, Zipped(y, qs));
let invC = InverseModI(c, modulus);
for (idx, yq) in Enumerated(y) {
let shiftedC = (invC <<< idx) % modulus;
Controlled ModularAddConstant([yq], (modulus, modulus - shiftedC, qs));
}
}
/// # Summary
/// Performs modular in-place addition of a classical constant into a
/// quantum register.
///
/// # Description
/// Given the classical constants `c` and `modulus`, and an input
/// quantum register |𝑦⟩, this operation
/// computes `(x+c) % modulus` into |𝑦⟩.
///
/// # Input
/// ## modulus
/// Modulus to use for modular addition
/// ## c
/// Constant to add to |𝑦⟩
/// ## y
/// Quantum register of target
internal operation ModularAddConstant(modulus : Int, c : Int, y : Qubit[])
: Unit is Adj + Ctl {
body (...) {
Controlled ModularAddConstant([], (modulus, c, y));
}
controlled (ctrls, ...) {
// We apply a custom strategy to control this operation instead of
// letting the compiler create the controlled variant for us in which
// the `Controlled` functor would be distributed over each operation
// in the body.
//
// Here we can use some scratch memory to save ensure that at most one
// control qubit is used for costly operations such as `AddConstant`
// and `CompareGreaterThenOrEqualConstant`.
if Length(ctrls) >= 2 {
use control = Qubit();
within {
Controlled X(ctrls, control);
} apply {
Controlled ModularAddConstant([control], (modulus, c, y));
}
} else {
use carry = Qubit();
Controlled AddConstant(ctrls, (c, y + [carry]));
Controlled Adjoint AddConstant(ctrls, (modulus, y + [carry]));
Controlled AddConstant([carry], (modulus, y));
Controlled CompareGreaterThanOrEqualConstant(ctrls, (c, y, carry));
}
}
}
/// # Summary
/// Performs in-place addition of a constant into a quantum register.
///
/// # Description
/// Given a non-empty quantum register |𝑦⟩ of length 𝑛+1 and a positive
/// constant 𝑐 < 2ⁿ, computes |𝑦 + c⟩ into |𝑦⟩.
///
/// # Input
/// ## c
/// Constant number to add to |𝑦⟩.
/// ## y
/// Quantum register of second summand and target; must not be empty.
internal operation AddConstant(c : Int, y : Qubit[]) : Unit is Adj + Ctl {
// We are using this version instead of the library version that is based
// on Fourier angles to show an advantage of sparse simulation in this sample.
let n = Length(y);
Fact(n > 0, "Bit width must be at least 1");
Fact(c >= 0, "constant must not be negative");
Fact(c < 2 ^ n, $"constant must be smaller than {2L ^ n}");
if c != 0 {
// If c has j trailing zeroes than the j least significant bits
// of y won't be affected by the addition and can therefore be
// ignored by applying the addition only to the other qubits and
// shifting c accordingly.
let j = NTrailingZeroes(c);
use x = Qubit[n - j];
within {
ApplyXorInPlace(c >>> j, x);
} apply {
IncByLE(x, y[j...]);
}
}
}
/// # Summary
/// Performs greater-than-or-equals comparison to a constant.
///
/// # Description
/// Toggles output qubit `target` if and only if input register `x`
/// is greater than or equal to `c`.
///
/// # Input
/// ## c
/// Constant value for comparison.
/// ## x
/// Quantum register to compare against.
/// ## target
/// Target qubit for comparison result.
///
/// # Reference
/// This construction is described in [Lemma 3, arXiv:2201.10200]
internal operation CompareGreaterThanOrEqualConstant(c : Int, x : Qubit[], target : Qubit)
: Unit is Adj+Ctl {
let bitWidth = Length(x);
if c == 0 {
X(target);
} elif c >= 2 ^ bitWidth {
// do nothing
} elif c == 2 ^ (bitWidth - 1) {
ApplyLowTCNOT(Tail(x), target);
} else {
// normalize constant
let l = NTrailingZeroes(c);
let cNormalized = c >>> l;
let xNormalized = x[l...];
let bitWidthNormalized = Length(xNormalized);
let gates = Rest(IntAsBoolArray(cNormalized, bitWidthNormalized));
use qs = Qubit[bitWidthNormalized - 1];
let cs1 = [Head(xNormalized)] + Most(qs);
let cs2 = Rest(xNormalized);
within {
for i in IndexRange(gates) {
(gates[i] ? ApplyAnd | ApplyOr)(cs1[i], cs2[i], qs[i]);
}
} apply {
ApplyLowTCNOT(Tail(qs), target);
}
}
}
/// # Summary
/// Internal operation used in the implementation of GreaterThanOrEqualConstant.
internal operation ApplyOr(control1 : Qubit, control2 : Qubit, target : Qubit) : Unit is Adj {
within {
ApplyToEachA(X, [control1, control2]);
} apply {
ApplyAnd(control1, control2, target);
X(target);
}
}
internal operation ApplyAnd(control1 : Qubit, control2 : Qubit, target : Qubit)
: Unit is Adj {
body (...) {
CCNOT(control1, control2, target);
}
adjoint (...) {
H(target);
if (M(target) == One) {
X(target);
CZ(control1, control2);
}
}
}
/// # Summary
/// Returns the number of trailing zeroes of a number
///
/// ## Example
/// ```qsharp
/// let zeroes = NTrailingZeroes(21); // = NTrailingZeroes(0b1101) = 0
/// let zeroes = NTrailingZeroes(20); // = NTrailingZeroes(0b1100) = 2
/// ```
internal function NTrailingZeroes(number : Int) : Int {
mutable nZeroes = 0;
mutable copy = number;
while (copy % 2 == 0) {
nZeroes += 1;
copy /= 2;
}
return nZeroes;
}
/// # Summary
/// An implementation for `CNOT` that when controlled using a single control uses
/// a helper qubit and uses `ApplyAnd` to reduce the T-count to 4 instead of 7.
internal operation ApplyLowTCNOT(a : Qubit, b : Qubit) : Unit is Adj+Ctl {
body (...) {
CNOT(a, b);
}
adjoint self;
controlled (ctls, ...) {
// In this application this operation is used in a way that
// it is controlled by at most one qubit.
Fact(Length(ctls) <= 1, "At most one control line allowed");
if IsEmpty(ctls) {
CNOT(a, b);
} else {
use q = Qubit();
within {
ApplyAnd(Head(ctls), a, q);
} apply {
CNOT(q, b);
}
}
}
controlled adjoint self;
}
Ejecución del estimador de recursos
El estimador de recursos ofrece seis parámetros de cúbit predefinidos, cuatro de los cuales tienen conjuntos de instrucciones basados en puertas y dos que tienen un conjunto de instrucciones Majorana. También ofrece dos floquet_code
En este ejemplo, ejecutará el estimador de recursos mediante el parámetro de cúbit qubit_gate_us_e3 y el código de corrección de errores cuánticos surface_code.
Seleccione Ver -> Paleta de comandos y escriba "recurso" que debe abrir la opción Q#: Calculate Resource Estimates (Calcular estimaciones de recursos). También puede hacer clic en Estimación en la lista de comandos que se muestran justo antes de la
Mainoperación. Seleccione esta opción para abrir la ventana del estimador de recursos.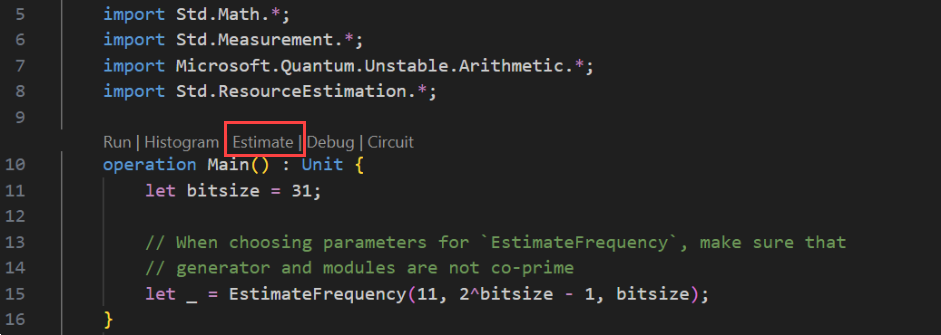
Puede seleccionar uno o varios tipos de parámetros de cúbit y códigos de corrección de errores para calcular los recursos. En este ejemplo, seleccione qubit_gate_us_e3 y haga clic en Aceptar.
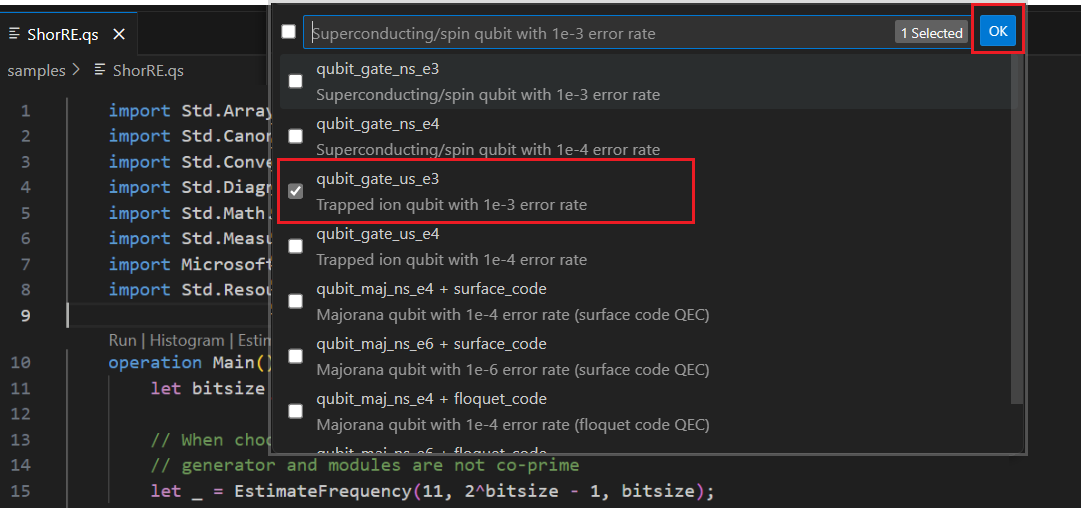
Especifique el presupuesto de errores o acepte el valor predeterminado 0,001. En este ejemplo, deje el valor predeterminado y presione Entrar.
Presione Entrar para aceptar el nombre de resultado predeterminado en función del nombre de archivo, en este caso, ShorRE.
Ver resultados
El estimador de recursos proporciona varias estimaciones para el mismo algoritmo, cada una de las cuales muestra inconvenientes entre el número de cúbits y el tiempo de ejecución. Comprender el equilibrio entre el tiempo de ejecución y la escala del sistema es uno de los aspectos más importantes de la estimación de recursos.
El resultado de la estimación de recursos se muestra en la ventana Estimación de Q#.
En la pestaña Resultados, se muestra un resumen de la estimación de recursos. Haga clic en el icono situado junto a la primera fila para seleccionar las columnas que desee mostrar. Puede seleccionar entre el nombre de ejecución, el tipo de estimación, el tipo de cúbit, el esquema qec, el presupuesto de errores, los cúbits lógicos, la profundidad lógica, la distancia del código, los estados de T, los generadores de T, la fracción de factoría de T, el tiempo de ejecución, rQOPS y los cúbits físicos.
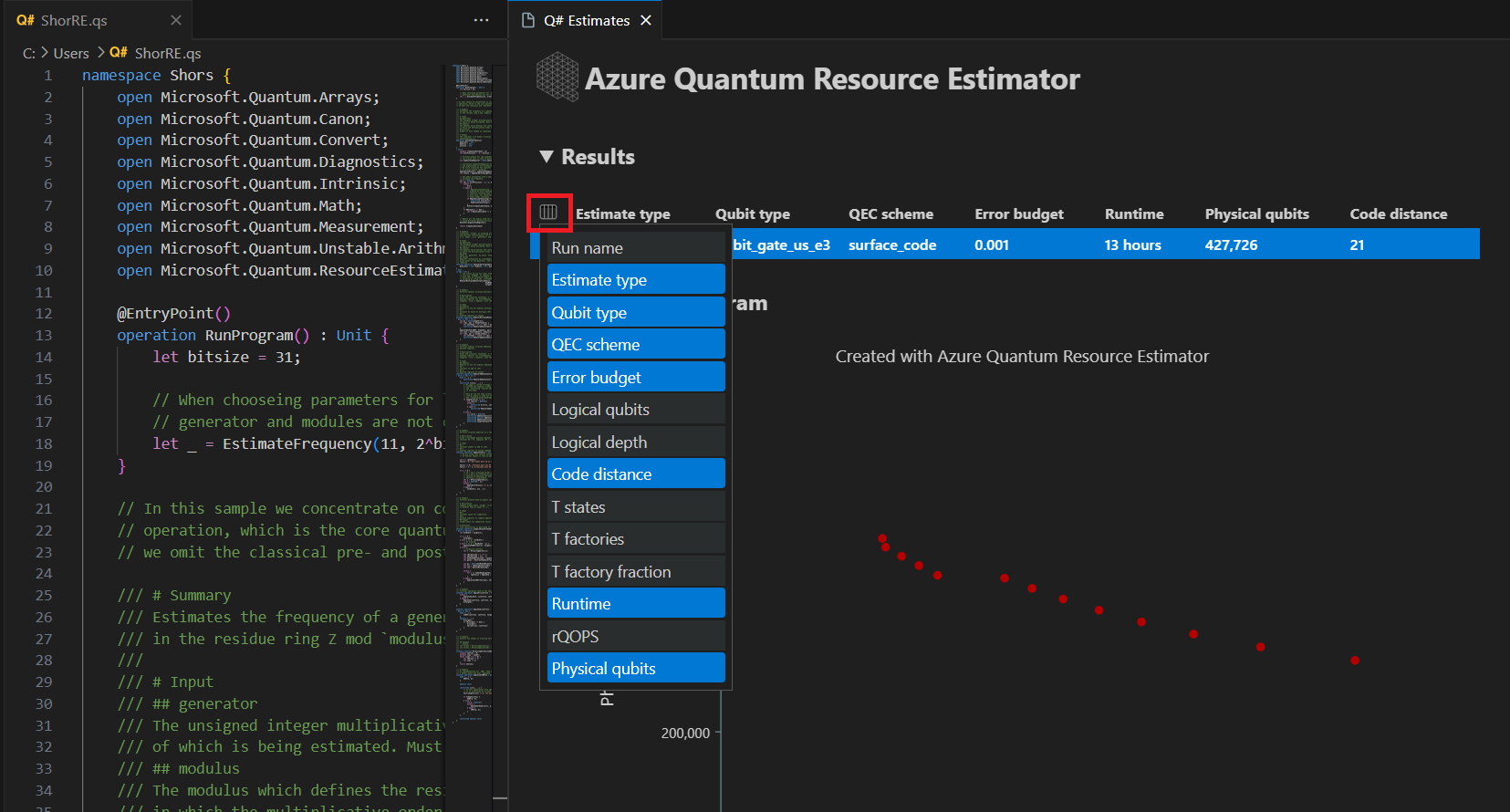
En la columna Tipo estimado de la tabla de resultados, puede ver el número de combinaciones óptimas de {número de cúbits, runtime} para el algoritmo. Estas combinaciones se pueden ver en el diagrama de tiempo espacial.
En el diagrama space-time se muestran los inconvenientes entre el número de cúbits físicos y el tiempo de ejecución del algoritmo. En este caso, el estimador de recursos encuentra 13 combinaciones óptimas diferentes de muchas miles posibles. Puede mantener el puntero sobre cada {número de cúbits, tiempo de ejecución} para ver los detalles de la estimación de recursos en ese momento.
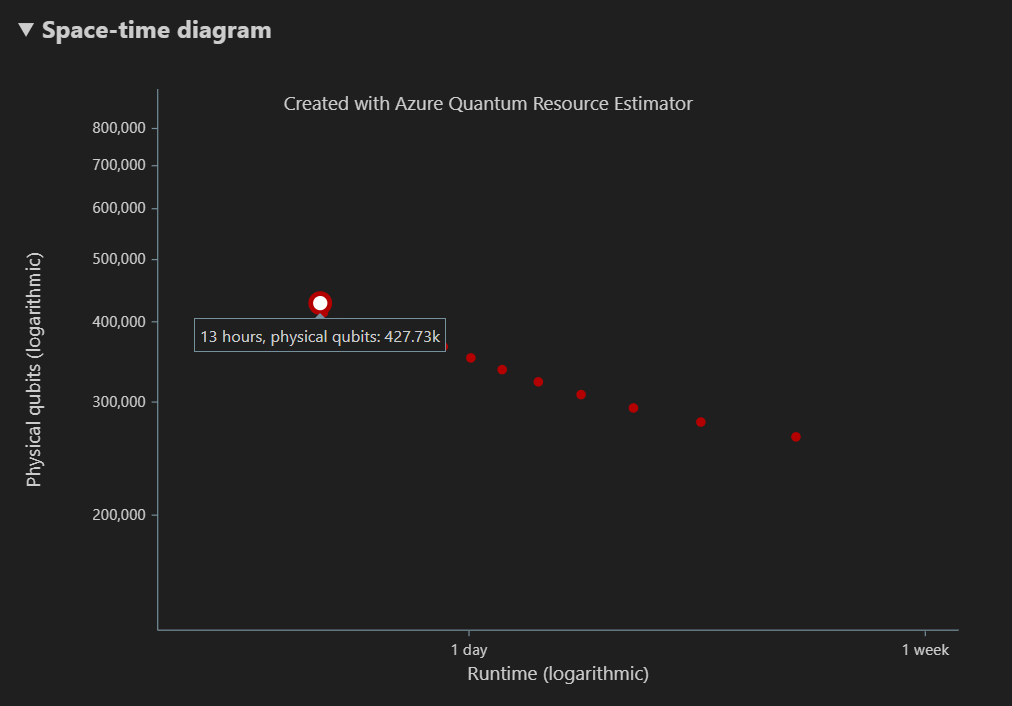
Para obtener más información, vea Diagrama de tiempo espaciador.
Nota:
Debe hacer clic en un punto del diagrama de tiempo espaciado, es decir, un {número de cúbits, un par runtime}, para ver el diagrama de espacio y los detalles de la estimación de recursos correspondiente a ese punto.
El diagrama space muestra la distribución de cúbits físicos usados para el algoritmo y las factorías de T, correspondientes a un par {número de cúbits, runtime}. Por ejemplo, si selecciona el punto más a la izquierda en el diagrama de tiempo espacial, el número de cúbits físicos necesarios para ejecutar el algoritmo se 427726, 196686 de los cuales son cúbits de algoritmo y 231040 de los cuales son cúbits de fábrica de T.
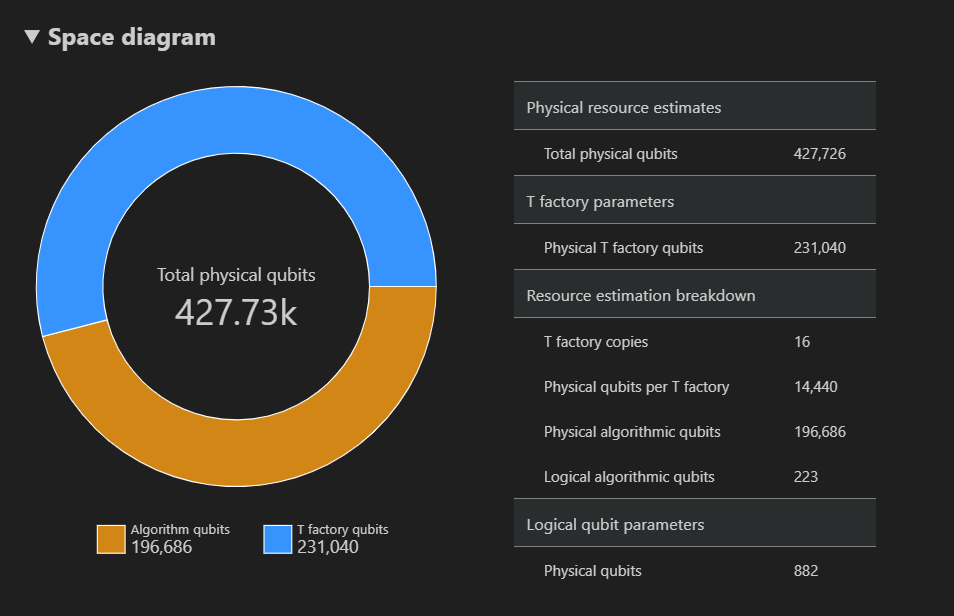
Por último, en la pestaña Estimaciones de recursos se muestra la lista completa de datos de salida del estimador de recursos correspondiente a un par {número de cúbits, runtime} . Se pueden inspeccionar los detalles de los costos contrayendo los grupos, que contienen más información. Por ejemplo, seleccione el punto más a la izquierda en el diagrama de tiempo espaciado y contraiga el grupo Parámetros cuánticos lógicos .
Parámetro de cúbit lógico Value Esquema de QEC surface_code Distancia del código 21 Cúbits físicos 882 Tiempo de ciclo lógico 13 milisegundos Tasa de errores de cúbit lógico 3,00E-13 Factor previo de cruce 0,03 Umbral de corrección de errores 0,01 Fórmula de tiempo de ciclo lógico (4 * twoQubitGateTime+ 2 *oneQubitMeasurementTime) *codeDistanceFórmula de cúbits físicos 2 * codeDistance*codeDistanceSugerencia
Haga clic en Mostrar filas de detalles para mostrar la descripción de cada salida de los datos del informe.
Para obtener más información, consulte los datos de informe completos del estimador de recursos.
Cambiar los target parámetros
Puede calcular el costo del mismo programa de Q# mediante otro tipo de cúbit, código de corrección de errores y presupuesto de errores. Abra la ventana Estimador de recursos seleccionando Ver -> Paleta de comandos y escriba Q#: Calculate Resource Estimates.
Seleccione cualquier otra configuración, por ejemplo, el parámetro qubit basado en Majorana, qubit_maj_ns_e6. Acepte el valor predeterminado del presupuesto de errores o escriba uno nuevo y presione Entrar. El estimador de recursos vuelve a ejecutar la estimación con los nuevos target parámetros.
Para obtener más información, consulte Target parámetros para el estimador de recursos.
Ejecución de varias configuraciones de parámetros
El estimador de recursos de Azure Quantum puede ejecutar varias configuraciones de parámetros y comparar los resultados de target la estimación de recursos.
Seleccione Ver-> Paleta de comandos o presione Ctrl+Mayús+P y escriba
Q#: Calculate Resource Estimates.Seleccione qubit_gate_us_e3, qubit_gate_us_e4, qubit_maj_ns_e4 + floquet_code y qubit_maj_ns_e6 + floquet_code y haga clic en Aceptar.
Acepte el valor predeterminado del presupuesto de errores 0.001 y presione Entrar.
Presione Entrar para aceptar el archivo de entrada, en este caso, ShorRE.qs.
En el caso de varias configuraciones de parámetros, los resultados se muestran en filas diferentes en la pestaña Resultados .
En el diagrama space-time se muestran los resultados de todas las configuraciones de parámetros. La primera columna de la tabla de resultados muestra la leyenda de cada configuración de parámetros. Puede mantener el puntero sobre cada punto para ver los detalles de la estimación de recursos en ese momento.
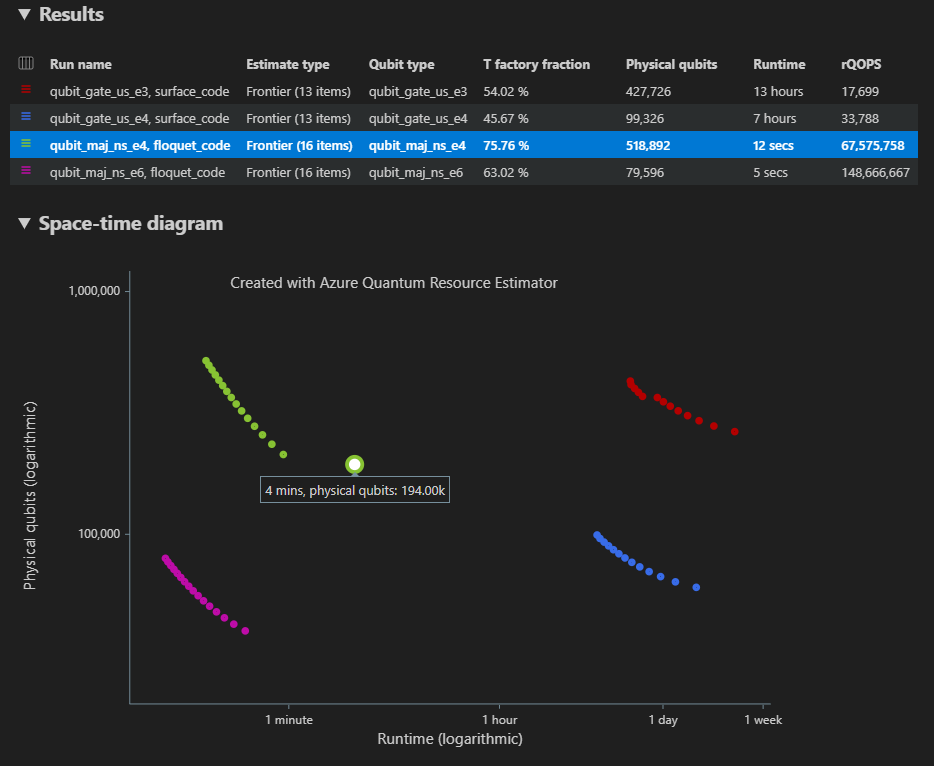
Haga clic en un punto {número de cúbits, runtime} del diagrama de tiempo de espacio para mostrar el diagrama de espacio y los datos de informe correspondientes.
Requisitos previos para Jupyter Notebook en VS Code
Un entorno de Python con Python y Pip instalados.
La versión más reciente de Visual Studio Code o abrir VS Code en la Web.
VS Code con el kit de desarrollo de Quantum, Python y extensiones de de Jupyter instaladas.
Los paquetes y
qsharpAzure Quantumqsharp_widgetsmás recientes.python -m pip install --upgrade qsharp qsharp_widgetso
!pip install --upgrade qsharp qsharp_widgets
Sugerencia
No es necesario tener una cuenta de Azure para ejecutar el estimador de recursos.
Creación del algoritmo cuántico
En VS Code, seleccione Ver > Paleta de comandos y seleccione Crear: Nuevo Jupyter Notebook.
En la parte superior derecha, VS Code detectará y mostrará la versión de Python y el entorno de Python virtual que se seleccionó para el cuaderno. Si tiene varios entornos de Python, es posible que tenga que seleccionar un kernel mediante el selector de kernel en la parte superior derecha. Si no se detectó ningún entorno, consulte Jupyter Notebooks in VS Code (Cuadernos de Jupyter Notebook en VS Code ) para obtener información de configuración.
En la primera celda del cuaderno, importe el paquete
qsharp.import qsharpAgregue una nueva celda y copie el código siguiente.
%%qsharp import Std.Arrays.*; import Std.Canon.*; import Std.Convert.*; import Std.Diagnostics.*; import Std.Math.*; import Std.Measurement.*; import Microsoft.Quantum.Unstable.Arithmetic.*; import Std.ResourceEstimation.*; operation RunProgram() : Unit { let bitsize = 31; // When choosing parameters for `EstimateFrequency`, make sure that // generator and modules are not co-prime let _ = EstimateFrequency(11, 2^bitsize - 1, bitsize); } // In this sample we concentrate on costing the `EstimateFrequency` // operation, which is the core quantum operation in Shors algorithm, and // we omit the classical pre- and post-processing. /// # Summary /// Estimates the frequency of a generator /// in the residue ring Z mod `modulus`. /// /// # Input /// ## generator /// The unsigned integer multiplicative order (period) /// of which is being estimated. Must be co-prime to `modulus`. /// ## modulus /// The modulus which defines the residue ring Z mod `modulus` /// in which the multiplicative order of `generator` is being estimated. /// ## bitsize /// Number of bits needed to represent the modulus. /// /// # Output /// The numerator k of dyadic fraction k/2^bitsPrecision /// approximating s/r. operation EstimateFrequency( generator : Int, modulus : Int, bitsize : Int ) : Int { mutable frequencyEstimate = 0; let bitsPrecision = 2 * bitsize + 1; // Allocate qubits for the superposition of eigenstates of // the oracle that is used in period finding. use eigenstateRegister = Qubit[bitsize]; // Initialize eigenstateRegister to 1, which is a superposition of // the eigenstates we are estimating the phases of. // We first interpret the register as encoding an unsigned integer // in little endian encoding. ApplyXorInPlace(1, eigenstateRegister); let oracle = ApplyOrderFindingOracle(generator, modulus, _, _); // Use phase estimation with a semiclassical Fourier transform to // estimate the frequency. use c = Qubit(); for idx in bitsPrecision - 1..-1..0 { within { H(c); } apply { // `BeginEstimateCaching` and `EndEstimateCaching` are the operations // exposed by Azure Quantum Resource Estimator. These will instruct // resource counting such that the if-block will be executed // only once, its resources will be cached, and appended in // every other iteration. if BeginEstimateCaching("ControlledOracle", SingleVariant()) { Controlled oracle([c], (1 <<< idx, eigenstateRegister)); EndEstimateCaching(); } R1Frac(frequencyEstimate, bitsPrecision - 1 - idx, c); } if MResetZ(c) == One { frequencyEstimate += 1 <<< (bitsPrecision - 1 - idx); } } // Return all the qubits used for oracle eigenstate back to 0 state // using Microsoft.Quantum.Intrinsic.ResetAll. ResetAll(eigenstateRegister); return frequencyEstimate; } /// # Summary /// Interprets `target` as encoding unsigned little-endian integer k /// and performs transformation |k⟩ ↦ |gᵖ⋅k mod N ⟩ where /// p is `power`, g is `generator` and N is `modulus`. /// /// # Input /// ## generator /// The unsigned integer multiplicative order ( period ) /// of which is being estimated. Must be co-prime to `modulus`. /// ## modulus /// The modulus which defines the residue ring Z mod `modulus` /// in which the multiplicative order of `generator` is being estimated. /// ## power /// Power of `generator` by which `target` is multiplied. /// ## target /// Register interpreted as little endian encoded which is multiplied by /// given power of the generator. The multiplication is performed modulo /// `modulus`. internal operation ApplyOrderFindingOracle( generator : Int, modulus : Int, power : Int, target : Qubit[] ) : Unit is Adj + Ctl { // The oracle we use for order finding implements |x⟩ ↦ |x⋅a mod N⟩. We // also use `ExpModI` to compute a by which x must be multiplied. Also // note that we interpret target as unsigned integer in little-endian // encoding. ModularMultiplyByConstant(modulus, ExpModI(generator, power, modulus), target); } /// # Summary /// Performs modular in-place multiplication by a classical constant. /// /// # Description /// Given the classical constants `c` and `modulus`, and an input /// quantum register |𝑦⟩, this operation /// computes `(c*x) % modulus` into |𝑦⟩. /// /// # Input /// ## modulus /// Modulus to use for modular multiplication /// ## c /// Constant by which to multiply |𝑦⟩ /// ## y /// Quantum register of target internal operation ModularMultiplyByConstant(modulus : Int, c : Int, y : Qubit[]) : Unit is Adj + Ctl { use qs = Qubit[Length(y)]; for (idx, yq) in Enumerated(y) { let shiftedC = (c <<< idx) % modulus; Controlled ModularAddConstant([yq], (modulus, shiftedC, qs)); } ApplyToEachCA(SWAP, Zipped(y, qs)); let invC = InverseModI(c, modulus); for (idx, yq) in Enumerated(y) { let shiftedC = (invC <<< idx) % modulus; Controlled ModularAddConstant([yq], (modulus, modulus - shiftedC, qs)); } } /// # Summary /// Performs modular in-place addition of a classical constant into a /// quantum register. /// /// # Description /// Given the classical constants `c` and `modulus`, and an input /// quantum register |𝑦⟩, this operation /// computes `(x+c) % modulus` into |𝑦⟩. /// /// # Input /// ## modulus /// Modulus to use for modular addition /// ## c /// Constant to add to |𝑦⟩ /// ## y /// Quantum register of target internal operation ModularAddConstant(modulus : Int, c : Int, y : Qubit[]) : Unit is Adj + Ctl { body (...) { Controlled ModularAddConstant([], (modulus, c, y)); } controlled (ctrls, ...) { // We apply a custom strategy to control this operation instead of // letting the compiler create the controlled variant for us in which // the `Controlled` functor would be distributed over each operation // in the body. // // Here we can use some scratch memory to save ensure that at most one // control qubit is used for costly operations such as `AddConstant` // and `CompareGreaterThenOrEqualConstant`. if Length(ctrls) >= 2 { use control = Qubit(); within { Controlled X(ctrls, control); } apply { Controlled ModularAddConstant([control], (modulus, c, y)); } } else { use carry = Qubit(); Controlled AddConstant(ctrls, (c, y + [carry])); Controlled Adjoint AddConstant(ctrls, (modulus, y + [carry])); Controlled AddConstant([carry], (modulus, y)); Controlled CompareGreaterThanOrEqualConstant(ctrls, (c, y, carry)); } } } /// # Summary /// Performs in-place addition of a constant into a quantum register. /// /// # Description /// Given a non-empty quantum register |𝑦⟩ of length 𝑛+1 and a positive /// constant 𝑐 < 2ⁿ, computes |𝑦 + c⟩ into |𝑦⟩. /// /// # Input /// ## c /// Constant number to add to |𝑦⟩. /// ## y /// Quantum register of second summand and target; must not be empty. internal operation AddConstant(c : Int, y : Qubit[]) : Unit is Adj + Ctl { // We are using this version instead of the library version that is based // on Fourier angles to show an advantage of sparse simulation in this sample. let n = Length(y); Fact(n > 0, "Bit width must be at least 1"); Fact(c >= 0, "constant must not be negative"); Fact(c < 2 ^ n, $"constant must be smaller than {2L ^ n}"); if c != 0 { // If c has j trailing zeroes than the j least significant bits // of y will not be affected by the addition and can therefore be // ignored by applying the addition only to the other qubits and // shifting c accordingly. let j = NTrailingZeroes(c); use x = Qubit[n - j]; within { ApplyXorInPlace(c >>> j, x); } apply { IncByLE(x, y[j...]); } } } /// # Summary /// Performs greater-than-or-equals comparison to a constant. /// /// # Description /// Toggles output qubit `target` if and only if input register `x` /// is greater than or equal to `c`. /// /// # Input /// ## c /// Constant value for comparison. /// ## x /// Quantum register to compare against. /// ## target /// Target qubit for comparison result. /// /// # Reference /// This construction is described in [Lemma 3, arXiv:2201.10200] internal operation CompareGreaterThanOrEqualConstant(c : Int, x : Qubit[], target : Qubit) : Unit is Adj+Ctl { let bitWidth = Length(x); if c == 0 { X(target); } elif c >= 2 ^ bitWidth { // do nothing } elif c == 2 ^ (bitWidth - 1) { ApplyLowTCNOT(Tail(x), target); } else { // normalize constant let l = NTrailingZeroes(c); let cNormalized = c >>> l; let xNormalized = x[l...]; let bitWidthNormalized = Length(xNormalized); let gates = Rest(IntAsBoolArray(cNormalized, bitWidthNormalized)); use qs = Qubit[bitWidthNormalized - 1]; let cs1 = [Head(xNormalized)] + Most(qs); let cs2 = Rest(xNormalized); within { for i in IndexRange(gates) { (gates[i] ? ApplyAnd | ApplyOr)(cs1[i], cs2[i], qs[i]); } } apply { ApplyLowTCNOT(Tail(qs), target); } } } /// # Summary /// Internal operation used in the implementation of GreaterThanOrEqualConstant. internal operation ApplyOr(control1 : Qubit, control2 : Qubit, target : Qubit) : Unit is Adj { within { ApplyToEachA(X, [control1, control2]); } apply { ApplyAnd(control1, control2, target); X(target); } } internal operation ApplyAnd(control1 : Qubit, control2 : Qubit, target : Qubit) : Unit is Adj { body (...) { CCNOT(control1, control2, target); } adjoint (...) { H(target); if (M(target) == One) { X(target); CZ(control1, control2); } } } /// # Summary /// Returns the number of trailing zeroes of a number /// /// ## Example /// ```qsharp /// let zeroes = NTrailingZeroes(21); // = NTrailingZeroes(0b1101) = 0 /// let zeroes = NTrailingZeroes(20); // = NTrailingZeroes(0b1100) = 2 /// ``` internal function NTrailingZeroes(number : Int) : Int { mutable nZeroes = 0; mutable copy = number; while (copy % 2 == 0) { nZeroes += 1; copy /= 2; } return nZeroes; } /// # Summary /// An implementation for `CNOT` that when controlled using a single control uses /// a helper qubit and uses `ApplyAnd` to reduce the T-count to 4 instead of 7. internal operation ApplyLowTCNOT(a : Qubit, b : Qubit) : Unit is Adj+Ctl { body (...) { CNOT(a, b); } adjoint self; controlled (ctls, ...) { // In this application this operation is used in a way that // it is controlled by at most one qubit. Fact(Length(ctls) <= 1, "At most one control line allowed"); if IsEmpty(ctls) { CNOT(a, b); } else { use q = Qubit(); within { ApplyAnd(Head(ctls), a, q); } apply { CNOT(q, b); } } } controlled adjoint self; }
Cálculo del algoritmo cuántico
Ahora, estime los recursos físicos para la operación RunProgram con los supuestos predeterminados. Agregue una nueva celda y copie el código siguiente.
result = qsharp.estimate("RunProgram()")
result
La función qsharp.estimate crea un objeto de resultado, que se puede usar para mostrar una tabla con el número global de recursos físicos. Puede inspeccionar los detalles de costos expandiendo los grupos, que tienen más información. Para obtener más información, consulte los datos de informe completos del estimador de recursos.
Por ejemplo, amplíe el grupo de parámetros de qubits lógicos para ver que la distancia del código es 21 y el número de qubits físicos es 882.
| Parámetro de cúbit lógico | Value |
|---|---|
| Esquema de QEC | surface_code |
| Distancia del código | 21 |
| Cúbits físicos | 882 |
| Tiempo de ciclo lógico | 8 milisegundos |
| Tasa de errores de cúbit lógico | 3,00E-13 |
| Factor previo de cruce | 0,03 |
| Umbral de corrección de errores | 0,01 |
| Fórmula de tiempo de ciclo lógico | (4 * twoQubitGateTime + 2 * oneQubitMeasurementTime) * codeDistance |
| Fórmula de cúbits físicos | 2 * codeDistance * codeDistance |
Sugerencia
Para obtener una versión más compacta de la tabla de salida, puede usar result.summary.
Diagrama de espacio
La distribución de cúbits físicos usados para el algoritmo y las fábricas T es un factor que puede afectar al diseño del algoritmo. Puede usar el paquete qsharp-widgets para visualizar esta distribución para comprender mejor los requisitos de espacio estimados para el algoritmo.
from qsharp-widgets import SpaceChart, EstimateDetails
SpaceChart(result)
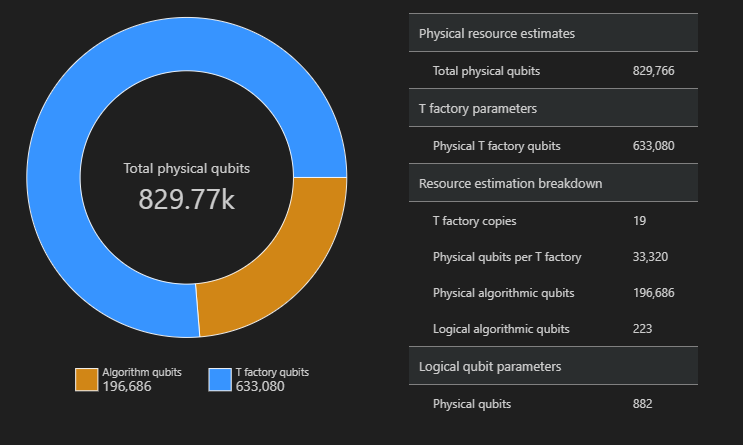
En este ejemplo, el número de cúbits físicos necesarios para ejecutar el algoritmo es 829766, 196686 de los cuales son cúbits de algoritmo y 633080 de los cuales son cúbits de fábrica T.
Cambio de los valores predeterminados y cálculo del algoritmo
Al enviar una solicitud de cálculo de recursos para el programa, puede especificar algunos parámetros opcionales. Use el jobParams campo para acceder a todos los target parámetros que se pueden pasar a la ejecución del trabajo y ver qué valores predeterminados se han asumido:
result['jobParams']
{'errorBudget': 0.001,
'qecScheme': {'crossingPrefactor': 0.03,
'errorCorrectionThreshold': 0.01,
'logicalCycleTime': '(4 * twoQubitGateTime + 2 * oneQubitMeasurementTime) * codeDistance',
'name': 'surface_code',
'physicalQubitsPerLogicalQubit': '2 * codeDistance * codeDistance'},
'qubitParams': {'instructionSet': 'GateBased',
'name': 'qubit_gate_ns_e3',
'oneQubitGateErrorRate': 0.001,
'oneQubitGateTime': '50 ns',
'oneQubitMeasurementErrorRate': 0.001,
'oneQubitMeasurementTime': '100 ns',
'tGateErrorRate': 0.001,
'tGateTime': '50 ns',
'twoQubitGateErrorRate': 0.001,
'twoQubitGateTime': '50 ns'}}
Puede ver que el estimador de recursos toma el modelo de cúbits qubit_gate_ns_e3, el código de corrección de errores surface_code y el presupuesto de errores 0,001 como valores predeterminados para el cálculo.
Estos son los target parámetros que se pueden personalizar:
errorBudget: el presupuesto general de errores permitido para el algoritmoqecScheme: el esquema de corrección de errores cuánticos (QEC)qubitParams: los parámetros de cúbit físicosconstraints: restricciones en el nivel de componente.distillationUnitSpecifications: las especificaciones de los algoritmos de destilación de fábricas de TestimateType: único o fronterizo
Para obtener más información, consulte Target parámetros para el estimador de recursos.
Cambio del modelo de cúbits
Puede calcular el costo del mismo algoritmo mediante el parámetro de cúbit basado en Majorana, qubitParams, "qubit_maj_ns_e6".
result_maj = qsharp.estimate("RunProgram()", params={
"qubitParams": {
"name": "qubit_maj_ns_e6"
}})
EstimateDetails(result_maj)
Cambio del esquema de corrección de errores cuánticos
Puede volver a ejecutar el trabajo de cálculo de recursos para el mismo ejemplo en los parámetros de cúbit basados en Majorana con un esquema QEC en código floquet, qecScheme.
result_maj = qsharp.estimate("RunProgram()", params={
"qubitParams": {
"name": "qubit_maj_ns_e6"
},
"qecScheme": {
"name": "floquet_code"
}})
EstimateDetails(result_maj)
Cambio del presupuesto de errores
A continuación, vuelva a ejecutar el mismo circuito cuántico con un errorBudget del 10 %.
result_maj = qsharp.estimate("RunProgram()", params={
"qubitParams": {
"name": "qubit_maj_ns_e6"
},
"qecScheme": {
"name": "floquet_code"
},
"errorBudget": 0.1})
EstimateDetails(result_maj)
Procesamiento por lotes con el estimador de recursos
El estimador de recursos de Azure Quantum permite ejecutar varias configuraciones de target parámetros y comparar los resultados. Esto resulta útil cuando desea comparar el coste de diferentes modelos de cúbits, esquemas QEC o presupuestos de error.
Puede realizar una estimación por lotes pasando una lista de target parámetros al
paramsparámetro de laqsharp.estimatefunción. Por ejemplo, ejecute el mismo algoritmo con los parámetros predeterminados y los parámetros de cúbit basados en Majorana con un esquema QEC de floquet.result_batch = qsharp.estimate("RunProgram()", params= [{}, # Default parameters { "qubitParams": { "name": "qubit_maj_ns_e6" }, "qecScheme": { "name": "floquet_code" } }]) result_batch.summary_data_frame(labels=["Gate-based ns, 10⁻³", "Majorana ns, 10⁻⁶"])Modelo Cúbits lógicos Profundidad lógica Estados T Distancia del código Generadores de T Fracción de generador de T Cúbits físicos rQOPS Tiempo de ejecución físico ns basados en puertas, 10⁻³ 223 3,64 M 4,70 M 21 19 76.30 % 829.77k 26,55 M 31 segundos ns basados en Majorana, 10⁻⁶ 223 3,64 M 4,70 M 5 19 63.02 % 79.60k 148,67 M 5 segundos También puede construir una lista de parámetros de estimación mediante la
EstimatorParamsclase .from qsharp.estimator import EstimatorParams, QubitParams, QECScheme, LogicalCounts labels = ["Gate-based µs, 10⁻³", "Gate-based µs, 10⁻⁴", "Gate-based ns, 10⁻³", "Gate-based ns, 10⁻⁴", "Majorana ns, 10⁻⁴", "Majorana ns, 10⁻⁶"] params = EstimatorParams(num_items=6) params.error_budget = 0.333 params.items[0].qubit_params.name = QubitParams.GATE_US_E3 params.items[1].qubit_params.name = QubitParams.GATE_US_E4 params.items[2].qubit_params.name = QubitParams.GATE_NS_E3 params.items[3].qubit_params.name = QubitParams.GATE_NS_E4 params.items[4].qubit_params.name = QubitParams.MAJ_NS_E4 params.items[4].qec_scheme.name = QECScheme.FLOQUET_CODE params.items[5].qubit_params.name = QubitParams.MAJ_NS_E6 params.items[5].qec_scheme.name = QECScheme.FLOQUET_CODEqsharp.estimate("RunProgram()", params=params).summary_data_frame(labels=labels)Modelo Cúbits lógicos Profundidad lógica Estados T Distancia del código Generadores de T Fracción de generador de T Cúbits físicos rQOPS Tiempo de ejecución físico μs basados en puertas, 10⁻³ 223 3,64 M 4,70 M 17 13 40,54 % 216,77 k 21,86 k 10 horas μs basados en puertas, 10⁻⁴ 223 3,64 M 4,70 M 9 14 43,17 % 63,57 k 41,30 k 5 horas ns basados en puertas, 10⁻³ 223 3,64 M 4,70 M 17 16 69,08 % 416,89 k 32,79 M 25 s ns basados en puertas, 10⁻⁴ 223 3,64 M 4,70 M 9 14 43,17 % 63,57 k 61,94 M 13 s ns basados en Majorana, 10⁻⁴ 223 3,64 M 4,70 M 9 19 82,75 % 501,48 k 82,59 M 10 s ns basados en Majorana, 10⁻⁶ 223 3,64 M 4,70 M 5 13 31,47 % 42,96 k 148,67 M 5 segundos
Ejecución de la estimación de la frontera de Pareto
Al calcular los recursos de un algoritmo, es importante tener en cuenta el equilibrio entre el número de cúbits físicos y el tiempo de ejecución del algoritmo. Podría considerar la asignación de tantos cúbits físicos como sea posible para reducir el tiempo de ejecución del algoritmo. Sin embargo, el número de cúbits físicos está limitado por el número de cúbits físicos disponibles en el hardware cuántico.
La estimación de la frontera de Pareto proporciona varias estimaciones para el mismo algoritmo, cada una con un equilibrio entre el número de cúbits y el tiempo de ejecución.
Para ejecutar el estimador de recursos mediante la estimación de frontera de Pareto, debe especificar el
"estimateType"target parámetro como"frontier". Por ejemplo, ejecute el mismo algoritmo con los parámetros de cúbit basados en Majorana con un código de superficie mediante la estimación de frontera de Pareto.result = qsharp.estimate("RunProgram()", params= {"qubitParams": { "name": "qubit_maj_ns_e4" }, "qecScheme": { "name": "surface_code" }, "estimateType": "frontier", # frontier estimation } )Puede usar la
EstimatesOverviewfunción para mostrar una tabla con los recuentos generales de recursos físicos. Haga clic en el icono situado junto a la primera fila para seleccionar las columnas que desee mostrar. Puede seleccionar entre el nombre de ejecución, el tipo de estimación, el tipo de cúbit, el esquema qec, el presupuesto de errores, los cúbits lógicos, la profundidad lógica, la distancia del código, los estados de T, los generadores de T, la fracción de factoría de T, el tiempo de ejecución, rQOPS y los cúbits físicos.from qsharp_widgets import EstimatesOverview EstimatesOverview(result)
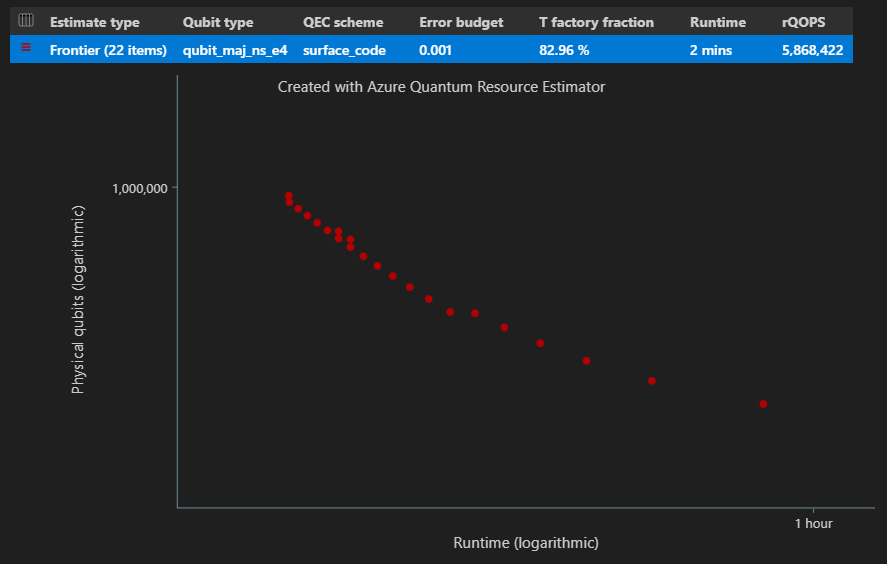
En la columna Tipo estimado de la tabla de resultados, puede ver el número de combinaciones diferentes de {número de cúbits, runtime} para el algoritmo. En este caso, el estimador de recursos encuentra 22 combinaciones óptimas diferentes de muchas miles posibles.
Diagrama de tiempo espaciador
La EstimatesOverview función también muestra el diagrama de tiempo espaciador del estimador de recursos.
El diagrama de tiempo espaciado muestra el número de cúbits físicos y el tiempo de ejecución del algoritmo para cada par {número de cúbits, runtime}. Puede mantener el puntero sobre cada punto para ver los detalles de la estimación de recursos en ese momento.
Procesamiento por lotes con estimación de frontera de Pareto
Para calcular y comparar varias configuraciones de target parámetros con estimación de frontera, agregue
"estimateType": "frontier",a los parámetros.result = qsharp.estimate( "RunProgram()", [ { "qubitParams": { "name": "qubit_maj_ns_e4" }, "qecScheme": { "name": "surface_code" }, "estimateType": "frontier", # Pareto frontier estimation }, { "qubitParams": { "name": "qubit_maj_ns_e6" }, "qecScheme": { "name": "floquet_code" }, "estimateType": "frontier", # Pareto frontier estimation }, ] ) EstimatesOverview(result, colors=["#1f77b4", "#ff7f0e"], runNames=["e4 Surface Code", "e6 Floquet Code"])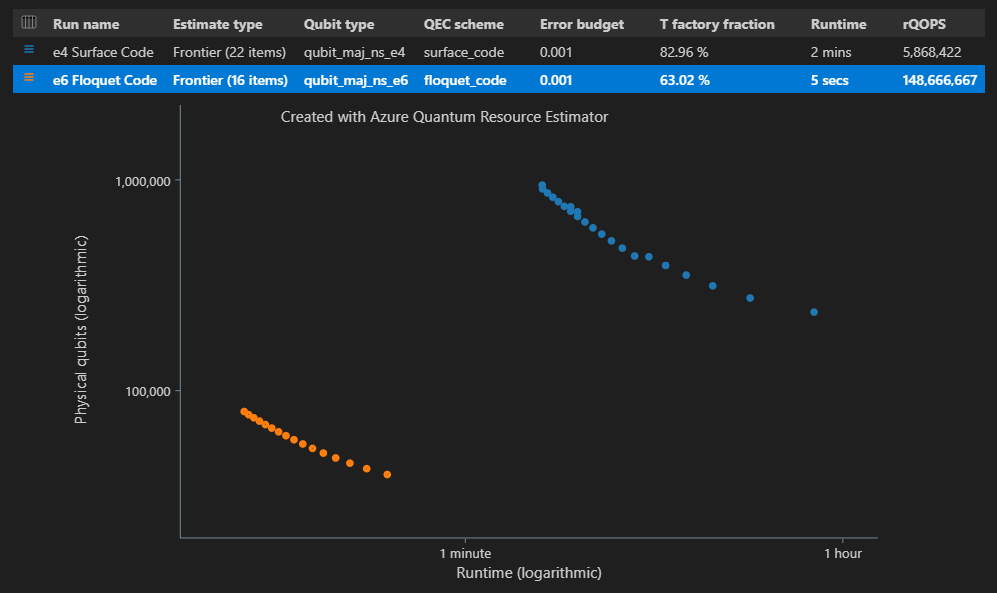
Nota:
Puede definir colores y nombres de ejecución para el diagrama de tiempo de cúbit mediante la
EstimatesOverviewfunción .Al ejecutar varias configuraciones de target parámetros mediante la estimación de frontera de Pareto, puede ver las estimaciones de recursos para un punto específico del diagrama de tiempo espaciado, es decir, para cada {número de cúbits, par runtime}. Por ejemplo, el código siguiente muestra el uso de detalles de estimación para la segunda ejecución (estimación de index=0) y el cuarto tiempo de ejecución (point index=3).
EstimateDetails(result[1], 4)También puede ver el diagrama de espacio para un punto específico del diagrama de tiempo espacial. Por ejemplo, el código siguiente muestra el diagrama de espacio para la primera ejecución de combinaciones (estimación de index=0) y el tercer tiempo de ejecución más corto (point index=2).
SpaceChart(result[0], 2)
Requisitos previos para Qiskit en VS Code
Un entorno de Python con Python y Pip instalados.
La versión más reciente de Visual Studio Code o abra Visual Studio Code en la web.
VS Code con el Kit de Desarrollo de Quantum , Python , y las extensiones de Jupyter instaladas.
Los paquetes de
qsharpyqsharp_widgetsyqiskitde Azure Quantum más recientes.python -m pip install --upgrade qsharp qsharp_widgets qiskito
!pip install --upgrade qsharp qsharp_widgets qiskit
Sugerencia
No es necesario tener una cuenta de Azure para ejecutar el estimador de recursos.
Crea un nuevo cuaderno de Jupyter
- En VS Code, seleccione Ver > Paleta de comandos y seleccione Crear: Nuevo Jupyter Notebook.
- En la parte superior derecha, VS Code detectará y mostrará la versión de Python y el entorno de Python virtual que se seleccionó para el cuaderno. Si tiene varios entornos de Python, es posible que tenga que seleccionar un kernel mediante el selector de kernel en la parte superior derecha. Si no se detectó ningún entorno, consulte Jupyter Notebooks in VS Code (Cuadernos de Jupyter Notebook en VS Code ) para obtener información de configuración.
Creación del algoritmo cuántico
En este ejemplo, se crea un circuito cuántico para un multiplicador basado en la construcción presentada en Ruiz-Perez y Garcia-Escartin (arXiv:1411.5949) que usa la transformación de Fourier cuántico para implementar la aritmética.
Puede ajustar el tamaño del multiplicador cambiando la bitwidth variable. La generación del circuito se ajusta en una función a la que se puede llamar con el bitwidth valor del multiplicador. La operación tendrá dos registros de entrada, cada uno del tamaño del objeto especificado bitwidthy un registro de salida que sea el doble del tamaño del especificado bitwidth. La función también imprimirá algunos recuentos de recursos lógicos para el multiplicador extraído directamente del circuito cuántico.
from qiskit.circuit.library import RGQFTMultiplier
def create_algorithm(bitwidth):
print(f"[INFO] Create a QFT-based multiplier with bitwidth {bitwidth}")
circ = RGQFTMultiplier(num_state_qubits=bitwidth)
return circ
Nota:
Si selecciona un kernel de Python y el módulo qiskit no se reconoce, intente seleccionar otro entorno de Python en el selector de kernel.
Cálculo del algoritmo cuántico
Cree una instancia del algoritmo mediante la create_algorithm función . Puede ajustar el tamaño del multiplicador cambiando la bitwidth variable.
bitwidth = 4
circ = create_algorithm(bitwidth)
Calcule los recursos físicos de esta operación mediante las suposiciones predeterminadas. Puede usar la llamada estimate, que se sobrecarga para aceptar un objeto QuantumCircuit de Qiskit.
from qsharp.estimator import EstimatorParams
from qsharp.interop.qiskit import estimate
params = EstimatorParams()
result = estimate(circ, params)
Como alternativa, puede usar el ResourceEstimatorBackend para realizar la estimación como lo hace el back-end existente.
from qsharp.interop.qiskit import ResourceEstimatorBackend
from qsharp.estimator import EstimatorParams
params = EstimatorParams()
backend = ResourceEstimatorBackend()
job = backend.run(circ, params)
result = job.result()
El objeto result contiene la salida del trabajo de estimación de recursos. Puede usar la función EstimateDetails para mostrar los resultados en un formato más legible.
from qsharp_widgets import EstimateDetails
EstimateDetails(result)
EstimateDetails función muestra una tabla con los recuentos generales de recursos físicos. Puede inspeccionar los detalles de costos expandiendo los grupos, que tienen más información. Para obtener más información, consulte los datos de informe completos del estimador de recursos.
Por ejemplo, si expande el grupo de los parámetros de cúbit lógicos, puede ver más fácilmente que la distancia del código de corrección de errores es 15.
| Parámetro de cúbit lógico | Value |
|---|---|
| Esquema de QEC | surface_code |
| Distancia del código | 15 |
| Cúbits físicos | 450 |
| Tiempo de ciclo lógico | 6us |
| Tasa de errores de cúbit lógico | 3.00E-10 |
| Factor previo de cruce | 0,03 |
| Umbral de corrección de errores | 0,01 |
| Fórmula de tiempo de ciclo lógico | (4 * twoQubitGateTime + 2 * oneQubitMeasurementTime) * codeDistance |
| Fórmula de cúbits físicos | 2 * codeDistance * codeDistance |
En el grupo Parámetros de cúbit físico, puede ver las propiedades de cúbit físicos que se han asumido para esta estimación. Por ejemplo, el tiempo para realizar una medición de un solo cúbit y una puerta de un solo cúbit se supone que son 100 ns y 50 ns, respectivamente.
Sugerencia
También puede acceder a la salida del estimador de recursos como diccionario de Python mediante el método result.data(). Por ejemplo, para acceder a los recuentos físicos result.data()["physicalCounts"].
Diagramas de espacio
La distribución de cúbits físicos usados para el algoritmo y las fábricas T es un factor que puede afectar al diseño del algoritmo. Puede visualizar esta distribución para comprender mejor los requisitos de espacio estimados para el algoritmo.
from qsharp_widgets import SpaceChart
SpaceChart(result)
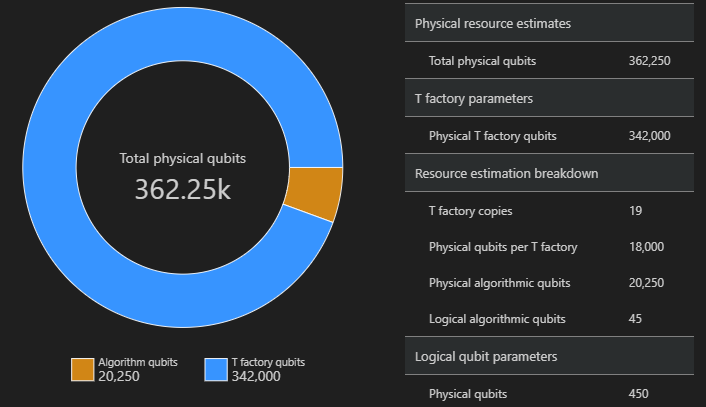
El diagrama de espacio muestra la proporción de cúbits de algoritmo y cúbits de fábrica de T. Tenga en cuenta que el número de copias de factorías de T, 19, contribuye al número de cúbits físicos para factorías de T según $\text{factorías de T} \cdot \text{cúbit físico por factoría de T}= 19 \cdot 18.000 = 342.000$.
Para obtener más información, consulte Estimación física de fábrica de T.
Cambio de los valores predeterminados y cálculo del algoritmo
Al enviar una solicitud de cálculo de recursos para el programa, puede especificar algunos parámetros opcionales. Use el jobParams campo para acceder a todos los valores que se pueden pasar a la ejecución del trabajo y ver qué valores predeterminados se han asumido:
result.data()["jobParams"]
{'errorBudget': 0.001,
'qecScheme': {'crossingPrefactor': 0.03,
'errorCorrectionThreshold': 0.01,
'logicalCycleTime': '(4 * twoQubitGateTime + 2 * oneQubitMeasurementTime) * codeDistance',
'name': 'surface_code',
'physicalQubitsPerLogicalQubit': '2 * codeDistance * codeDistance'},
'qubitParams': {'instructionSet': 'GateBased',
'name': 'qubit_gate_ns_e3',
'oneQubitGateErrorRate': 0.001,
'oneQubitGateTime': '50 ns',
'oneQubitMeasurementErrorRate': 0.001,
'oneQubitMeasurementTime': '100 ns',
'tGateErrorRate': 0.001,
'tGateTime': '50 ns',
'twoQubitGateErrorRate': 0.001,
'twoQubitGateTime': '50 ns'}}
Estos son los target parámetros que se pueden personalizar:
errorBudget: el presupuesto general de errores permitidoqecScheme: el esquema de corrección de errores cuánticos (QEC)qubitParams: los parámetros de cúbit físicosconstraints: restricciones en el nivel de componente.distillationUnitSpecifications: las especificaciones de los algoritmos de destilación de fábricas de T
Para obtener más información, consulte Target parámetros para el estimador de recursos.
Cambio del modelo de cúbits
A continuación, calcule el costo del mismo algoritmo mediante el parámetro qubit basado en Majorana. qubit_maj_ns_e6
qubitParams = {
"name": "qubit_maj_ns_e6"
}
result = backend.run(circ, qubitParams).result()
Puede inspeccionar los recuentos físicos mediante programación. Por ejemplo, puede explorar detalles sobre la factoría de T que se creó para ejecutar el algoritmo.
result.data()["tfactory"]
{'eccDistancePerRound': [1, 1, 5],
'logicalErrorRate': 1.6833177305222897e-10,
'moduleNamePerRound': ['15-to-1 space efficient physical',
'15-to-1 RM prep physical',
'15-to-1 RM prep logical'],
'numInputTstates': 20520,
'numModulesPerRound': [1368, 20, 1],
'numRounds': 3,
'numTstates': 1,
'physicalQubits': 16416,
'physicalQubitsPerRound': [12, 31, 1550],
'runtime': 116900.0,
'runtimePerRound': [4500.0, 2400.0, 110000.0]}
Nota:
De forma predeterminada, el tiempo de ejecución se muestra en nanosegundos.
Puede usar estos datos para generar algunas explicaciones sobre cómo las factorías de T generan los estados T necesarios.
data = result.data()
tfactory = data["tfactory"]
breakdown = data["physicalCounts"]["breakdown"]
producedTstates = breakdown["numTfactories"] * breakdown["numTfactoryRuns"] * tfactory["numTstates"]
print(f"""A single T factory produces {tfactory["logicalErrorRate"]:.2e} T states with an error rate of (required T state error rate is {breakdown["requiredLogicalTstateErrorRate"]:.2e}).""")
print(f"""{breakdown["numTfactories"]} copie(s) of a T factory are executed {breakdown["numTfactoryRuns"]} time(s) to produce {producedTstates} T states ({breakdown["numTstates"]} are required by the algorithm).""")
print(f"""A single T factory is composed of {tfactory["numRounds"]} rounds of distillation:""")
for round in range(tfactory["numRounds"]):
print(f"""- {tfactory["numUnitsPerRound"][round]} {tfactory["unitNamePerRound"][round]} unit(s)""")
A single T factory produces 1.68e-10 T states with an error rate of (required T state error rate is 2.77e-08).
23 copies of a T factory are executed 523 time(s) to produce 12029 T states (12017 are required by the algorithm).
A single T factory is composed of 3 rounds of distillation:
- 1368 15-to-1 space efficient physical unit(s)
- 20 15-to-1 RM prep physical unit(s)
- 1 15-to-1 RM prep logical unit(s)
Cambio del esquema de corrección de errores cuánticos
Ahora, vuelva a ejecutar el trabajo de estimación de recursos para el mismo ejemplo en los parámetros de cúbit basados en Majorana con un esquema QEC floqued, qecScheme.
params = {
"qubitParams": {"name": "qubit_maj_ns_e6"},
"qecScheme": {"name": "floquet_code"}
}
result_maj_floquet = backend.run(circ, params).result()
EstimateDetails(result_maj_floquet)
Cambio del presupuesto de errores
Vamos a volver a ejecutar el mismo circuito cuántico con un errorBudget 10 %.
params = {
"errorBudget": 0.01,
"qubitParams": {"name": "qubit_maj_ns_e6"},
"qecScheme": {"name": "floquet_code"},
}
result_maj_floquet_e1 = backend.run(circ, params).result()
EstimateDetails(result_maj_floquet_e1)
Nota:
Si tiene algún problema al trabajar con el estimador de recursos, consulte la página Solución de problemas o póngase en contacto con AzureQuantumInfo@microsoft.com.