¿Qué es el entrelazamiento?
El entrelazamiento es una de las características clave de la mecánica cuántica que la distingue de la mecánica clásica. ¿Qué es el entrelazamiento? ¿Cómo funciona? ¿Y por qué es tan importante para la información cuántica?
En esta unidad, veremos cómo definir y describir el entrelazamiento cuántico y comprender por qué es un recurso tan eficaz para la computación cuántica.
Descripción del entrelazamiento cuántico
Imagine que tiene dos cúbits, $A$ y $B$. Los cúbits son independientes entre sí, lo que significa que la información sobre el estado del cúbit $A$, sea cual sea, pertenece solo al cúbit $A$. Del mismo modo, la información sobre el estado del cúbit $B$ pertenece a cúbit $B$. Puede describir el estado de cada cúbit. En este caso, los cúbits no están entrelazados porque no comparten ninguna información.
Ahora imagine que entrelaza los cúbits (aprenderá a hacerlo más adelante). Si los cúbits $A$ y $B$ están entrelazados, la información sobre el estado del cúbit $A$ no es independiente del estado de $B$. Cuando está entrelazada, la información se comparte entre ambos cúbits y no hay ninguna manera de deducir el estado del cúbit $A$ o el estado del cúbit $B$. Solo puede describir el estado del sistema global, no el estado de los cúbits individuales.
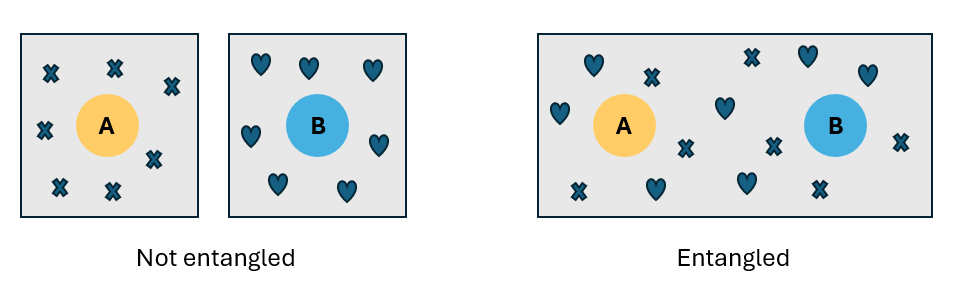
El entrelazamiento es una correlación cuántica entre dos o más partículas. Si dos partículas están entrelazadas, no se pueden describir de forma independiente, sino solo como un sistema entero.
Descripción del entrelazamiento cuántico
Imagine dos cúbits $A$ y $B$ de forma que el estado de $\ket{\phi}$ del sistema global sea:
$$\ket{\phi}=\frac1{\sqrt2}(\ket{0_A 0_B}+ \ket{1_A 1_B})$$
Nota:
En notación Dirac, $\ket{0_A 0_B}=|0\rangle_\text{A}|0\rangle_\text{B}$. La primera posición corresponde al primer cúbit y la segunda posición corresponde al segundo cúbit.
$\ket{\phi}$ del sistema global está en una superposición de los estados $|00\rangle$ y $|11\rangle$. Si mide ambos cúbits, solo se pueden dar dos resultados: $\ket{{00}$ y $\ket{{11}$, y cada uno tiene la misma probabilidad de $\frac{1}{{2}$.
¿Pero cuál es el estado individual del cúbit $A$? ¿Y del cúbit $B$? Si intenta describir el estado del cúbit $A$ sin tener en cuenta el estado del cúbit $B$, se producirá un error. Los subsistemas $A$ y $B$ están entrelazados, lo que significa que están correlacionados y no se pueden describir de forma independiente.
Sugerencia
Si está familiarizado con la notación de álgebra y Dirac, un buen ejercicio es intentar modificar el estado $\ket{\phi}$ para obtener algo parecido al estado del cúbit $A$ multiplicado por el estado del cúbit $B$. Si intenta expandir el paréntesis, obtenga el factor común, etc., y verá que no es posible.
$\ket{\phi}$ del estado cuántico es un estado entrelazado especial denominado estado Bell. Hay cuatro estados de Bell.
$$\ket{\phi^{+}}=\frac1{\sqrt2}\ket{{00} + \frac1{\sqrt2}\ket{{11}$$$$\ket{\phi^{-}}=\frac1{\sqrt2}\ket{00} - \frac1{\sqrt2}\ket{11}$$$$\ket{\psi^{+}}=\frac1{\sqrt2}\ket{{01} + \frac1{\sqrt2}\ket{{10}$$$$\ket{\psi^{-}}=\frac1{\sqrt2}\ket{01} - \frac1{\sqrt2}\ket{10}$$
Uso del entrelazamiento como un recurso
En este momento, puede preguntarse cuál es la importancia del entrelazamiento.
Cuando dos partículas están entrelazadas, los subsistemas se correlacionan y no se pueden describir de forma independiente. Pero esta es la parte interesante: los resultados de la medición también se correlacionan. Es decir: cualquier operación que ocurra con el estado de un cúbit de un par entrelazado también afecta al estado del otro cúbit.
Por ejemplo, considere el estado $\ket{\phi^{+}}$,
$$\ket{\phi^{+}}=\frac1{\sqrt2}\ket{{00} + \frac1{\sqrt2}\ket{{11}$$
Si mide ambos cúbits, obtendrá $|00\rangle$ o $|11\rangle$ con la misma probabilidad. Hay cero probabilidad de obtener los estados $|01\rangle$ y $|10\rangle$.
¿Pero qué ocurre si solo mide un cúbit?
Si solo mide el cúbit $A$ y obtiene el estado $|0\rangle$, significa que el sistema global se contrae al estado $\ket{00}$. Este es el único resultado posible, ya que la probabilidad de medir $|01\rangle$ es cero.
Por lo tanto, sin medir el cúbit $B$, puede tener la certeza de que el segundo cúbit también está en estado $|0\rangle$. Los resultados de la medición se correlacionan porque los cúbits están entrelazados.
El entrelazamiento puede existir entre dos partículas incluso si están separadas por grandes distancias. Esta correlación es más fuerte que cualquier correlación clásica y es un recurso clave para las tareas de procesamiento de información cuántica, como la teletransportación cuántica, la criptografía cuántica y la computación cuántica.