Partager via

Guide pratique pour contrôler le remplissage d’une forme composite

  • Article

La propriété FillRule d’un GeometryGroup ou d’un PathGeometry, spécifie une « règle » utilisée par la forme composite pour déterminer si un point donné fait partie de la géométrie. Il existe deux valeurs possibles pour FillRule: EvenOdd et Nonzero. Les sections suivantes décrivent comment utiliser ces deux règles.

EvenOdd : Cette règle détermine si un point se trouve dans la zone de remplissage en dessinant un rayon de ce point à l’infini dans n’importe quelle direction et en comptant le nombre de segments de chemin dans la forme donnée que le rayon croise. Si ce nombre est impair, le point est à l’intérieur ; si même, le point est en dehors.

Par exemple, le code XAML ci-dessous crée une forme composite composée d’une série d’anneaux concentriques (cible) avec un FillRule défini sur EvenOdd.

<Path Stroke="Black" StrokeThickness="1" Fill="#CCCCFF">
  <Path.Data>
    <GeometryGroup FillRule="EvenOdd">
      <EllipseGeometry RadiusX="50" RadiusY="50" Center="75,75" />
      <EllipseGeometry RadiusX="70" RadiusY="70" Center="75,75" />
      <EllipseGeometry RadiusX="100" RadiusY="100" Center="75,75" />
      <EllipseGeometry RadiusX="120" RadiusY="120" Center="75,75" />
    </GeometryGroup>
  </Path.Data>
</Path>

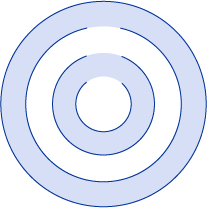
L’illustration suivante montre la forme créée dans l’exemple précédent.

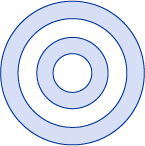
Un cercle composé d’anneaux concentriques de série avec des couleurs alternées.

Dans l’illustration précédente, notez que le centre et le troisième anneau ne sont pas remplis. Cela est dû au fait qu’un rayon dessiné à partir de n’importe quel point dans l’un de ces deux anneaux passe par un nombre pair de segments. Consultez l’illustration suivante :

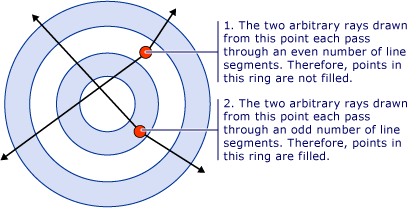
Diagramme montrant les rayons EvenOdd dessinés dans le cercle.

NonZero : Cette règle détermine si un point se trouve dans la zone de remplissage du chemin en dessinant un rayon de ce point à l’infini dans n’importe quelle direction, puis en examinant les endroits où un segment de la forme traverse le rayon. Commencez avec un compte de zéro, ajoutez un chaque fois qu’un segment traverse le rayon de gauche à droite et soustrayez un chaque fois qu’un segment traverse le rayon de droite à gauche. Après avoir compté les croisements, si le résultat est égal à zéro, le point est à l'extérieur du chemin. Sinon, c’est à l’intérieur.

<Path Stroke="Black" StrokeThickness="1" Fill="#CCCCFF">
  <Path.Data>
    <GeometryGroup FillRule="NonZero">
      <EllipseGeometry RadiusX="50" RadiusY="50" Center="75,75" />
      <EllipseGeometry RadiusX="70" RadiusY="70" Center="75,75" />
      <EllipseGeometry RadiusX="100" RadiusY="100" Center="75,75" />
      <EllipseGeometry RadiusX="120" RadiusY="120" Center="75,75" />
    </GeometryGroup>
  </Path.Data>
</Path>

À l’aide de l’exemple précédent, une valeur de Nonzero pour FillRule donne l’illustration suivante en conséquence :

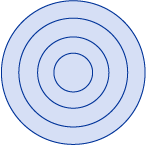
Cercle composé d’un anneau concentrique de série rempli de la même couleur.

Comme vous pouvez le voir, tous les anneaux sont remplis. Cela est dû au fait que tous les segments sont orientés dans la même direction et qu’un rayon dessiné à partir de n’importe quel point traversera un ou plusieurs segments et que la somme des intersections ne sera pas égale à zéro. Par exemple, dans l’illustration suivante, les flèches rouges représentent la direction dans laquelle les segments sont tracés et la flèche blanche représente un rayon arbitraire qui part d’un point dans le cercle le plus intérieur. À compter d’une valeur égale à zéro, pour chaque segment que le rayon traverse, une valeur d’une valeur est ajoutée, car le segment traverse le rayon de gauche à droite.

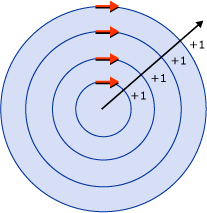
Diagramme montrant la valeur de la propriété FillRule égale à Nonzero.

Pour mieux illustrer le comportement de Nonzero règle, une forme plus complexe avec des segments s’exécutant dans différentes directions est nécessaire. Le code XAML ci-dessous crée une forme similaire à l’exemple précédent, sauf qu’elle est créée avec un PathGeometry plutôt qu’un EllipseGeometry qui crée quatre arcs concentriques plutôt que des cercles concentriques entièrement fermés.

<Path Stroke="Black" StrokeThickness="1" Fill="#CCCCFF">
  <Path.Data>
    <GeometryGroup FillRule="NonZero">
      <PathGeometry>
        <PathGeometry.Figures>

          <!-- Inner Ring -->
          <PathFigure StartPoint="10,120">
            <PathFigure.Segments>
              <PathSegmentCollection>
                <ArcSegment Size="50,50" IsLargeArc="True" SweepDirection="CounterClockwise" Point="25,120" />
              </PathSegmentCollection>
            </PathFigure.Segments>
          </PathFigure>

          <!-- Second Ring -->
          <PathFigure StartPoint="10,100">
            <PathFigure.Segments>
              <PathSegmentCollection>
                <ArcSegment Size="70,70" IsLargeArc="True" SweepDirection="CounterClockwise" Point="25,100" />
              </PathSegmentCollection>
            </PathFigure.Segments>
          </PathFigure>

          <!-- Third Ring (Not part of path) -->
          <PathFigure StartPoint="10,70">
            <PathFigure.Segments>
              <PathSegmentCollection>
                <ArcSegment Size="100,100" IsLargeArc="True" SweepDirection="CounterClockwise" Point="25,70" />
              </PathSegmentCollection>
            </PathFigure.Segments>
          </PathFigure>

          <!-- Outer Ring -->
          <PathFigure StartPoint="10,300">
            <PathFigure.Segments>
              <ArcSegment Size="130,130" IsLargeArc="True" SweepDirection="Clockwise" Point="25,300" />
            </PathFigure.Segments>
          </PathFigure>
        </PathGeometry.Figures>
      </PathGeometry>
    </GeometryGroup>
  </Path.Data>
</Path>

L’illustration suivante montre la forme créée dans l’exemple précédent.

Un cercle composé d’un anneau concentrique de série avec des couleurs alternées avec le troisième arc non rempli.

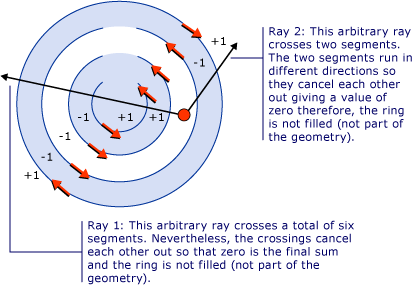
Notez que le troisième arc du centre n’est pas rempli. L’illustration suivante montre pourquoi c’est le cas. Dans l’illustration, les flèches rouges représentent la direction que les segments sont dessinés. Les deux flèches blanches représentent deux rayons arbitraires qui se déplacent d’un point dans la région « non remplie ». Comme on peut le voir à partir de l’illustration, la somme des valeurs d’un rayon donné qui traverse les segments dans son chemin est égale à zéro. Comme défini ci-dessus, une somme de zéro signifie que le point ne fait pas partie de la géométrie (et non une partie du remplissage), tandis qu’une somme qui n’est pas zéro, y compris une valeur négative, fait partie de la géométrie.

Diagramme montrant des rayons arbitraires franchissant des segments.

Note

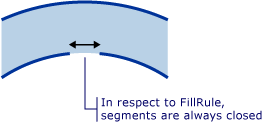
À des fins de FillRule, toutes les formes sont considérées comme fermées. S’il y a un écart dans un segment, dessinez une ligne imaginaire pour la fermer. Dans l’exemple ci-dessus, il existe de petites lacunes dans les anneaux. Étant donné cela, on peut s’attendre à ce qu’un rayon qui traverse l’écart donne un résultat différent qu’un rayon se déplaçant dans une autre direction. Vous trouverez ci-dessous une illustration agrandie de l’une de ces lacunes et du « segment imaginaire » (segment dessiné à des fins d’application du FillRule) qui le ferme.

Diagramme montrant les segments FillRule qui sont toujours fermés.

Exemple

Voir aussi