Résultats des modèles Machine Learning
Cet article traite des matrices de confusion, des problèmes de classification et de la précision des modèles de Machine Learning (ML). Le but est d’améliorer votre compréhension de la précision des résultats de prédiction ML. Le public cible comprend des ingénieurs, des analystes et des gestionnaires qui souhaitent développer leurs connaissances et leurs compétences en science des données.
Matrice de confusion
Une fois qu’un problème de ML supervisé est formé sur un jeu de données historiques, il est testé à l’aide de données qui ne sont pas conservées dans le processus de formation. De cette manière, vous pouvez comparer les prédictions du modèle formé avec les valeurs réelles. La matrice de confusion fournit un moyen d’évaluer le succès d’un problème de classification et où il fait des erreurs (c’est-à-dire où il devient "confus").
Par exemple, votre objectif est de prédire si un animal de compagnie est un chien ou un chat, sur la base de certains attributs physiques et comportementaux. Si vous disposez d’un jeu de données de test contenant 30 chiens et 20 chats, la matrice de confusion peut ressembler à l’illustration suivante.

Les nombres dans les cellules vertes représentent des prédictions correctes. Comme vous pouvez le voir, le modèle a prédit correctement un pourcentage plus élevé de chats réels. La précision globale du modèle est facile à calculer. Dans ce cas, c’est 42 ÷ 50, soit 0,84.
Classificateurs multi-classes dans une matrice de confusion
La plupart des discussions sur la matrice de confusion se concentrent sur les classificateurs binaires, comme dans l’exemple précédent. Ce cas est un cas particulier où d’autres métriques peuvent être envisagées, telles que la sensibilité et le rappel.
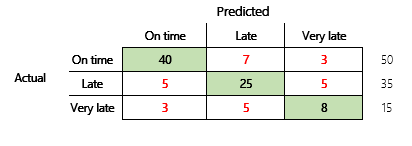
Ensuite, nous examinerons un problème de classification pour un scénario financier à trois états. Le modèle prédit si une facture client sera payée à temps, en retard ou très tard. Par exemple, sur 100 factures tests, 50 sont payées à temps, 35 sont payées en retard et 15 sont payées très tard. Dans ce cas, un modèle peut produire une matrice de confusion semblable à l’illustration suivante.
 ]
]
Une matrice de confusion fournit beaucoup plus d’informations qu’une simple métrique de précision. Cependant, c’est encore relativement facile à comprendre. Une matrice de confusion vous indique si vous avez un ensemble de données équilibré où les classes de résultats ont des nombres similaires. Pour le scénario multi-classes, il vous indique à quelle distance une prédiction peut être lorsque les classes de sortie sont ordinales, comme dans l’exemple précédent sur les paiements des clients.
Précision du modèle
Différentes métriques de précision ont l’avantage de quantifier la qualité du modèle.
La précision étant une métrique facile à comprendre, c’est un bon point de départ pour expliquer un modèle à d’autres personnes, en particulier aux utilisateurs du modèle qui ne sont pas des spécialistes des données. Aucune compréhension des statistiques n’est requise pour comprendre l’exactitude du modèle. Lorsqu’une matrice de confusion est disponible, elle fournit des informations supplémentaires sur les performances du modèle.
Cependant, pour une compréhension plus approfondie, il convient de noter plusieurs contraintes associés à la précision. L’utilité de la métrique dépend du contexte du problème. Une question qui se pose souvent en relation avec les performances du modèle est : « Quel est le modèle ? » Cependant, la réponse à cette question n’est pas nécessairement simple. Considérez la matrice de confusion suivante (modèle 2).
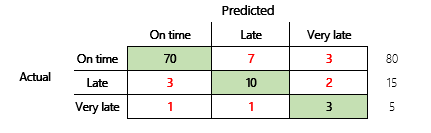
Un calcul rapide montre que la précision de ce modèle est de (70 + 10 + 3) ÷ 100, ou 0,83. En apparence, ce résultat semble meilleur que celui du modèle multi-classes précédent (modèle 1), qui a une précision de 0,73. Mais est-ce mieux ?
Pour commencer à répondre à cette question, considérez l’exactitude d’une supposition naïve. Pour un problème de classification, une simple estimation prédira toujours la classe la plus courante. Pour le modèle 1, cette estimation sera "ponctuelle" et produira une précision de 0,50. L’estimation pour le modèle 2 sera "ponctuelle" et produira une précision de 0,80. Comme le modèle 1 améliore la supposition naïve de 0,73 – 0,50 = 0,23, tandis que le modèle 2 améliore la supposition naïve de 0,83 – 0,80 = 0,03, le modèle 1 est un meilleur modèle, même s’il a une précision moindre. Le calcul révèle qu’une évaluation efficace de la qualité d’un modèle nécessite plus de contexte que la valeur de précision.
Un autre aspect mérite d’être noté. Prenons un scénario dans lequel un test médical est utilisé pour détecter une maladie chez un patient. Ce problème est un problème de classification binaire où un résultat positif indique que le patient a la maladie. Dans ce scénario, vous devez réfléchir à l’impact des erreurs suivantes :
- Faux positifs, où le test indique qu’une patiente a la maladie, mais que la patiente ne l’a pas vraiment.
- Faux négatifs, où le test indique qu’un patient a la maladie, mais que la patiente ne l’a pas vraiment.
De toute évidence, les deux types d’erreur ne sont pas souhaitables, mais laquelle est pire ? Encore une fois, cela dépend. Dans le cas d’une maladie potentiellement mortelle qui nécessite un traitement rapide, la minimisation des faux négatifs (avec un peu de chance, suivie de tests supplémentaires) est prioritaire. Dans d’autres situations moins critiques, les créateurs de modèles peuvent plutôt minimiser les faux positifs. Quoi qu’il en soit, une conclusion raisonnable est que pour déterminer efficacement la qualité d’un modèle, vous devez disposer de plus d’informations qu’une mesure de précision n’en fournit.
Recommandations
La précision est un outil important pour communiquer avec des spécialistes du domaine qui ne sont pas familiarisés avec les statistiques. Cependant, pour rendre les informations utiles, il est essentiel que le contexte supplémentaire soit fourni avec la valeur de précision.
Pour le scénario de prédiction de paiement, vous pouvez définir une cible pour le modèle ML qui inclut des facteurs dans différents comportements de paiement. L’objectif est que le modèle s’améliore sur une estimation naïve en réduisant le nombre de réponses incorrectes d’au moins 50 pour cent. En d’autres termes, vous voulez une précision cible qui divise la différence entre la précision d’une estimation naïve et 100 %.
Le tableau suivant résume ce principe pour les matrices de confusion de cet article.
| Modèle | Supposition naïve | Cible | Précision du modèle | L’objectif est-il atteint ? |
|---|---|---|---|---|
| Modèle 1 | 0.50 | 0.75 | 0.73 | Presque. Ce modèle améliore considérablement la supposition. |
| Modèle 2 | 0.80 | 0.90 | 0.83 | Non Une amélioration est nécessaire. |
Précision de classification F1
La considération finale dans cet article est une mesure plus avancée des performances de classification ML, connue sous le nom de précision F1.
Avant que la précision F1 ne puisse être définie, deux mesures supplémentaires doivent être introduites : la précision et le rappel. La précision indique combien du nombre total de prédictions spécifiées comme positives sont correctement affectées. Cette métrique est également connue sous le nom de valeur prédictive positive. Le rappel est le nombre total de cas positifs réels qui ont été correctement prédits. Cette métrique est également connue sous le nom de sensibilité.
Dans la matrice de confusion de l’illustration précédente, ces métriques sont calculées de la manière suivante :
- Précision = TP ÷ (TP + FP)
- Rappel = TP ÷ (TP + FN)
La mesure F1 combine précision et rappel. Le résultat est la moyenne harmonique des deux valeurs. Il est calculé comme suit :
- F1 = 2 × (Précision × Rappel) ÷ (Précision + Rappel)
Regardons un exemple concret. Plus tôt dans cet article, il y avait un exemple de modèle qui prédisait si un animal était un chien ou un chat. L’illustration est répétée ici.
Voici les résultats si "Chien" est utilisé comme réponse positive.
- Précision = 24 ÷ (24 + 2) = 0,9231
- Rappel = 24 ÷ (24 + 6) = 0,8
- F1 = 2 × (0,9231 × 0,8) ÷ (0,9231 + 0,8) = 0,8572
Comme vous pouvez le voir, la valeur F1 se situe entre les valeurs de précision et de rappel.
Bien que la précision F1 ne soit pas aussi facile à comprendre, elle ajoute de la nuance au nombre de précision de base. Cela peut également aider avec des jeux de données déséquilibrés, comme le montre la discussion suivante.
La section Précision du modèle de cet article a comparé les deux matrices de confusion suivantes. Même si le premier modèle était moins précis, il a été considéré comme un modèle plus utile car il montrait plus d’amélioration que l’estimation par défaut d’un paiement à temps.


Voyons comment ces deux modèles se comparent lorsque le score F1 est utilisé. Le score F1 prend en compte la précision et le rappel pour chaque état, et le calcul de la macro F1 fait ensuite la moyenne du score F1 à travers les états pour déterminer un score F1 global. Il existe d’autres variantes de F1, mais il est plus intéressant de considérer la version macro, étant donné la considération égale qui est accordée aux trois états.
Pour simplifier les calculs, des exemples de tableaux ont été créés pour correspondre aux valeurs réelles et prévues. Ces tableaux utilisaient la bibliothèque de métriques de sklearn en Python pour calculer les valeurs. Voici le résultat.
| Modèle | Supposition naïve | Précision | Macro F1 |
|---|---|---|---|
| Modèle 1 | 0.5 | 0.73 | 0.67 |
| Modèle 2 | 0.80 | 0.83 | 0.66 |
Pour plus de détails sur le fonctionnement de ce calcul, voici le rapport de classification sklearn.metrics pour le modèle 1. Les trois états, "À l’heure", "En retard" et "Très tard", sont représentés par les lignes étiquetées 1, 2 et 3, respectivement. La moyenne de la macro n’est que la moyenne de la colonne "f1-score".
| précision | rappel | f1-score | |
|---|---|---|---|
| 1 | 0.83 | 0.80 | 0.82 |
| 2 | 0.68 | 0.71 | 0.69 |
| 3 | 0.50 | 0.50 | 0.50 |
Comme le montrent ces résultats, les deux modèles ont des scores de précision macro F1 presque identiques. Dans ce cas et dans bien d’autres, la précision F1 fournit un meilleur indicateur de la capacité d’un modèle. Pour ce qui est de la précision, l’interprétation des résultats nécessite que vous compreniez ce qu’il est le plus important de prendre en compte dans le modèle.
