Transformations de matrice dans SkiaSharp
Découvrez plus en détail les transformations SkiaSharp avec la matrice de transformation polyvalente
Toutes les transformations appliquées à l’objet SKCanvas sont consolidées dans une seule instance de la SKMatrix structure. Il s’agit d’une matrice de transformation 3 par 3 standard similaire à celles de tous les systèmes graphiques 2D modernes.
Comme vous l’avez vu, vous pouvez utiliser des transformations dans SkiaSharp sans connaître la matrice de transformation, mais la matrice de transformation est importante du point de vue théorique, et il est crucial lors de l’utilisation de transformations pour modifier des chemins ou pour gérer les entrées tactiles complexes, qui sont présentées dans cet article et la suivante.

La matrice de transformation actuelle appliquée à celle-ci SKCanvas est disponible à tout moment en accédant à la propriété en lecture seule TotalMatrix . Vous pouvez définir une nouvelle matrice de transformation à l’aide de la SetMatrix méthode, et vous pouvez restaurer cette matrice de transformation en valeurs par défaut en appelant ResetMatrix.
Le seul autre SKCanvas membre qui fonctionne directement avec la transformation de matrice du canevas est Concat celui qui concatène deux matrices en les multipliant ensemble.
La matrice de transformation par défaut est la matrice d’identité et se compose de 1 dans les cellules diagonales et de 0 partout ailleurs :
| 1 0 0 | | 0 1 0 | | 0 0 1 |
Vous pouvez créer une matrice d’identité à l’aide de la méthode statique SKMatrix.MakeIdentity :
SKMatrix matrix = SKMatrix.MakeIdentity();
Le SKMatrix constructeur par défaut ne retourne pas de matrice d’identité. Elle retourne une matrice avec toutes les cellules définies sur zéro. N’utilisez pas le SKMatrix constructeur, sauf si vous envisagez de définir ces cellules manuellement.
Lorsque SkiaSharp affiche un objet graphique, chaque point (x, y) est effectivement converti en matrice de 1 par 3 avec un 1 dans la troisième colonne :
| x y 1 |
Cette matrice de 1 à 3 représente un point tridimensionnel avec la coordonnée Z définie sur 1. Il existe des raisons mathématiques (décrites plus loin) pour lesquelles une transformation de matrice à deux dimensions nécessite de travailler en trois dimensions. Vous pouvez considérer cette matrice 1 par 3 comme représentant un point dans un système de coordonnées 3D, mais toujours sur le plan 2D où Z est égal à 1.
Cette matrice de 1 à 3 est ensuite multipliée par la matrice de transformation, et le résultat est le point rendu sur le canevas :
| 1 0 0 |
| x y 1 | × | 0 1 0 | = | x' y' z' |
| 0 0 1 |
À l’aide de la multiplication de matrices standard, les points convertis sont les suivants :
x' = x
y' = y
z' = 1
C’est la transformation par défaut.
Lorsque la Translate méthode est appelée sur l’objetSKCanvas, les arguments et ty les tx arguments de la Translate méthode deviennent les deux premières cellules de la troisième ligne de la matrice de transformation :
| 1 0 0 | | 0 1 0 | | tx ty 1 |
La multiplication est désormais la suivante :
| 1 0 0 |
| x y 1 | × | 0 1 0 | = | x' y' z' |
| tx ty 1 |
Voici les formules de transformation :
x' = x + tx
y' = y + ty
Les facteurs de mise à l’échelle ont une valeur par défaut de 1. Lorsque vous appelez la Scale méthode sur un nouvel SKCanvas objet, la matrice de transformation résultante contient les arguments et sy les sx arguments dans les cellules diagonales :
| sx 0 0 |
| x y 1 | × | 0 sy 0 | = | x' y' z' |
| 0 0 1 |
Les formules de transformation sont les suivantes :
x' = sx · x
y' = sy · y
La matrice de transformation après appel Skew contient les deux arguments des cellules de matrice adjacentes aux facteurs de mise à l’échelle :
│ 1 ySkew 0 │
| x y 1 | × │ xSkew 1 0 │ = | x' y' z' |
│ 0 0 1 │
Les formules de transformation sont les suivantes :
x' = x + xSkew · y
y' = ySkew · x + y
Pour un appel à RotateDegrees ou RotateRadians pour un angle de α, la matrice de transformation est la suivante :
│ cos(α) sin(α) 0 │
| x y 1 | × │ –sin(α) cos(α) 0 │ = | x' y' z' |
│ 0 0 1 │
Voici les formules de transformation :
x' = cos(α) · x - sin(α) · y
y' = sin(α) · x - cos(α) · y
Lorsque α est de 0 degrés, il s’agit de la matrice d’identité. Lorsque α est de 180 degrés, la matrice de transformation est la suivante :
| –1 0 0 | | 0 –1 0 | | 0 0 1 |
Une rotation de 180 degrés équivaut à faire glisser un objet horizontalement et verticalement, ce qui est également accompli en définissant des facteurs d’échelle de –1.
Tous ces types de transformations sont classés comme des transformations affine . Les transformations affine n’impliquent jamais la troisième colonne de la matrice, qui reste aux valeurs par défaut de 0, 0 et 1. L’article Non-Affine Transforms traite des transformations non affines.
Multiplication de matrice
L’un des avantages importants de l’utilisation de la matrice de transformation est que les transformations composites peuvent être obtenues par multiplication de matrices, souvent appelées concaténation dans la documentation SkiaSharp. La plupart des méthodes SKCanvas liées à la transformation font référence à « pré-concaténation » ou « pré-concat ». Cela fait référence à l’ordre de multiplication, qui est important, car la multiplication de matrices n’est pas commutative.
Par exemple, la documentation de la Translate méthode indique qu’elle « pré-concate la matrice actuelle avec la traduction spécifiée », tandis que la documentation de la Scale méthode indique qu’elle « pré-concate la matrice actuelle avec l’échelle spécifiée ».
Cela signifie que la transformation spécifiée par l’appel de méthode est le multiplicateur (opérande de gauche) et que la matrice de transformation actuelle est le multiplicand (opérande de droite).
Supposons que cela Translate soit appelé suivi de Scale:
canvas.Translate(tx, ty);
canvas.Scale(sx, sy);
La Scale transformation est multipliée par la Translate transformation de la matrice de transformation composite :
| sx 0 0 | | 1 0 0 | | sx 0 0 | | 0 sy 0 | × | 0 1 0 | = | 0 sy 0 | | 0 0 1 | | tx ty 1 | | tx ty 1 |
Scale peut être appelé avant Translate ceci :
canvas.Scale(sx, sy);
canvas.Translate(tx, ty);
Dans ce cas, l’ordre de la multiplication est inversé et les facteurs de mise à l’échelle sont effectivement appliqués aux facteurs de traduction :
| 1 0 0 | | sx 0 0 | | sx 0 0 | | 0 1 0 | × | 0 sy 0 | = | 0 sy 0 | | tx ty 1 | | 0 0 1 | | tx·sx ty·sy 1 |
Voici la Scale méthode avec un point croisé dynamique :
canvas.Scale(sx, sy, px, py);
Cela équivaut aux appels de traduction et d’échelle suivants :
canvas.Translate(px, py);
canvas.Scale(sx, sy);
canvas.Translate(–px, –py);
Les trois matrices de transformation sont multipliées dans l’ordre inverse à partir de la façon dont les méthodes apparaissent dans le code :
| 1 0 0 | | sx 0 0 | | 1 0 0 | | sx 0 0 | | 0 1 0 | × | 0 sy 0 | × | 0 1 0 | = | 0 sy 0 | | –px –py 1 | | 0 0 1 | | px py 1 | | px–px·sx py–py·sy 1 |
The SKMatrix Structure
La SKMatrix structure définit neuf propriétés de type float en lecture/écriture correspondant aux neuf cellules de la matrice de transformation :
│ ScaleX SkewY Persp0 │ │ SkewX ScaleY Persp1 │ │ TransX TransY Persp2 │
SKMatrix définit également une propriété nommée Values de type float[]. Cette propriété peut être utilisée pour définir ou obtenir les neuf valeurs d’une capture dans l’ordre ScaleX, , SkewX, TransXSkewY, ScaleY, , TransY, Persp0et Persp1Persp2.
Les cellules et les cellules Persp1sont abordées dans l’article Non-Affine Transforms.Persp2Persp0 Si ces cellules ont leurs valeurs par défaut de 0, 0 et 1, la transformation est multipliée par un point de coordonnées comme suit :
│ ScaleX SkewY 0 │
| x y 1 | × │ SkewX ScaleY 0 │ = | x' y' z' |
│ TransX TransY 1 │
x' = ScaleX · x + SkewX · y + TransX
y' = SkewX · x + ScaleY · y + TransY
z' = 1
Il s’agit de la transformation affine bidimensionnelle complète. La transformation affine conserve les lignes parallèles, ce qui signifie qu’un rectangle n’est jamais transformé en autre chose qu’un parallélisme.
La SKMatrix structure définit plusieurs méthodes statiques pour créer SKMatrix des valeurs. Toutes les valeurs renvoyées SKMatrix sont les suivantes :
MakeTranslationMakeScaleMakeScaleavec un point croisé dynamiqueMakeRotationpour un angle en radiansMakeRotationpour un angle en radians avec un point croisé dynamiqueMakeRotationDegreesMakeRotationDegreesavec un point croisé dynamiqueMakeSkew
SKMatrix définit également plusieurs méthodes statiques qui concatènent deux matrices, ce qui signifie de les multiplier. Ces méthodes sont nommées Concat, PostConcatet PreConcatil existe deux versions de chacune d’elles. Ces méthodes n’ont aucune valeur de retour ; Ils référencent plutôt des valeurs existantes SKMatrix par le biais ref d’arguments. Dans l’exemple suivant, A, Bet R (pour « result ») sont toutes les SKMatrix valeurs.
Les deux Concat méthodes sont appelées comme suit :
SKMatrix.Concat(ref R, A, B);
SKMatrix.Concat(ref R, ref A, ref B);
Ces opérations effectuent la multiplication suivante :
R = B × A
Les autres méthodes n’ont que deux paramètres. Le premier paramètre est modifié et, lors de l’appel de méthode, contient le produit des deux matrices. Les deux PostConcat méthodes sont appelées comme suit :
SKMatrix.PostConcat(ref A, B);
SKMatrix.PostConcat(ref A, ref B);
Ces appels effectuent l’opération suivante :
A = A × B
Les deux PreConcat méthodes sont similaires :
SKMatrix.PreConcat(ref A, B);
SKMatrix.PreConcat(ref A, ref B);
Ces appels effectuent l’opération suivante :
A = B × A
Les versions de ces méthodes avec tous les ref arguments sont légèrement plus efficaces dans l’appel des implémentations sous-jacentes, mais il peut être déroutant pour quelqu’un qui lit votre code et en supposant que tout élément avec un ref argument est modifié par la méthode. De plus, il est souvent pratique de passer un argument résultant de l’une Make des méthodes, par exemple :
SKMatrix result;
SKMatrix.Concat(result, SKMatrix.MakeTranslation(100, 100),
SKMatrix.MakeScale(3, 3));
Cela crée la matrice suivante :
│ 3 0 0 │ │ 0 3 0 │ │ 100 100 1 │
Il s’agit de la transformation d’échelle multipliée par la transformation de traduction. Dans ce cas particulier, la SKMatrix structure fournit un raccourci avec une méthode nommée SetScaleTranslate:
SKMatrix R = new SKMatrix();
R.SetScaleTranslate(3, 3, 100, 100);
Il s’agit de l’une des rares fois où il est sûr d’utiliser le SKMatrix constructeur. La SetScaleTranslate méthode définit les neuf cellules de la matrice. Il est également sûr d’utiliser le SKMatrix constructeur avec les méthodes et RotateDegrees statiques Rotate :
SKMatrix R = new SKMatrix();
SKMatrix.Rotate(ref R, radians);
SKMatrix.Rotate(ref R, radians, px, py);
SKMatrix.RotateDegrees(ref R, degrees);
SKMatrix.RotateDegrees(ref R, degrees, px, py);
Ces méthodes ne concatènent pas une transformation de rotation vers une transformation existante. Les méthodes définissent toutes les cellules de la matrice. Elles sont fonctionnellement identiques aux méthodes et MakeRotationDegrees aux MakeRotation méthodes, sauf qu’elles n’instancient pas la SKMatrix valeur.
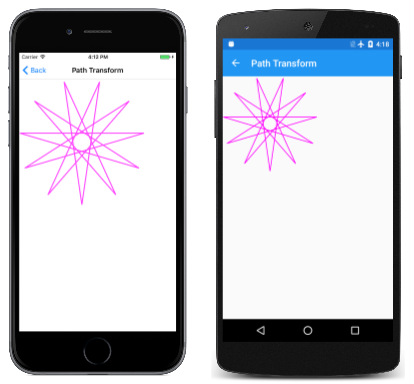
Supposons que vous disposez d’un SKPath objet que vous souhaitez afficher, mais que vous préférez qu’il ait une orientation un peu différente ou un point central différent. Vous pouvez modifier toutes les coordonnées de ce chemin en appelant la Transform méthode d’un SKPathSKMatrix argument. La page Transformation de chemin d’accès montre comment procéder. La PathTransform classe fait référence à l’objet HendecagramPath dans un champ, mais utilise son constructeur pour appliquer une transformation à ce chemin d’accès :
public class PathTransformPage : ContentPage
{
SKPath transformedPath = HendecagramArrayPage.HendecagramPath;
public PathTransformPage()
{
Title = "Path Transform";
SKCanvasView canvasView = new SKCanvasView();
canvasView.PaintSurface += OnCanvasViewPaintSurface;
Content = canvasView;
SKMatrix matrix = SKMatrix.MakeScale(3, 3);
SKMatrix.PostConcat(ref matrix, SKMatrix.MakeRotationDegrees(360f / 22));
SKMatrix.PostConcat(ref matrix, SKMatrix.MakeTranslation(300, 300));
transformedPath.Transform(matrix);
}
...
}
L’objet HendecagramPath a un centre à (0, 0), et les 11 points de l’étoile s’étendent vers l’extérieur de ce centre de 100 unités dans toutes les directions. Cela signifie que le chemin a des coordonnées positives et négatives. La page Path Transform préfère travailler avec une étoile trois fois plus grande et avec toutes les coordonnées positives. De plus, il ne veut pas qu’un point de l’étoile pointe droit vers le haut. Il veut plutôt qu’un point de l’étoile pointe droit vers le bas. (Étant donné que l’étoile a 11 points, elle ne peut pas avoir les deux.) Cela nécessite une rotation de l’étoile de 360 degrés divisé par 22.
Le constructeur génère un SKMatrix objet à partir de trois transformations distinctes à l’aide de la PostConcat méthode avec le modèle suivant, où A, B et C sont des instances de SKMatrix:
SKMatrix matrix = A;
SKMatrix.PostConcat(ref A, B);
SKMatrix.PostConcat(ref A, C);
Il s’agit d’une série de multiplications successives, de sorte que le résultat est le suivant :
A × B × C
Les multiplications consécutives aident à comprendre ce que fait chaque transformation. La transformation d’échelle augmente la taille des coordonnées de chemin d’accès par un facteur de 3, de sorte que les coordonnées vont de –300 à 300. La transformation de rotation fait pivoter l’étoile autour de son origine. La transformation de traduction la déplace ensuite de 300 pixels vers la droite et vers le bas, de sorte que toutes les coordonnées deviennent positives.
Il existe d’autres séquences qui produisent la même matrice. Voici un autre :
SKMatrix matrix = SKMatrix.MakeRotationDegrees(360f / 22);
SKMatrix.PostConcat(ref matrix, SKMatrix.MakeTranslation(100, 100));
SKMatrix.PostConcat(ref matrix, SKMatrix.MakeScale(3, 3));
Cela fait pivoter le chemin autour de son centre en premier, puis le traduit à 100 pixels vers la droite et vers le bas afin que toutes les coordonnées soient positives. L’étoile est ensuite augmentée par rapport à son nouveau coin supérieur gauche, qui est le point (0, 0).
Le PaintSurface gestionnaire peut simplement afficher ce chemin d’accès :
public class PathTransformPage : ContentPage
{
...
void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
SKImageInfo info = args.Info;
SKSurface surface = args.Surface;
SKCanvas canvas = surface.Canvas;
canvas.Clear();
using (SKPaint paint = new SKPaint())
{
paint.Style = SKPaintStyle.Stroke;
paint.Color = SKColors.Magenta;
paint.StrokeWidth = 5;
canvas.DrawPath(transformedPath, paint);
}
}
}
Il apparaît dans le coin supérieur gauche du canevas :
Le constructeur de ce programme applique la matrice au chemin d’accès avec l’appel suivant :
transformedPath.Transform(matrix);
Le chemin d’accès ne conserve pas cette matrice en tant que propriété. Au lieu de cela, il applique la transformation à toutes les coordonnées du chemin. Si Transform elle est appelée à nouveau, la transformation est appliquée à nouveau, et la seule façon dont vous pouvez revenir en arrière consiste à appliquer une autre matrice qui annule la transformation. Heureusement, la SKMatrix structure définit une TryInvert méthode qui obtient la matrice qui inverse une matrice donnée :
SKMatrix inverse;
bool success = matrix.TryInverse(out inverse);
La méthode est appelée TryInverse , car toutes les matrices ne sont pas inversées, mais une matrice non inversée n’est pas susceptible d’être utilisée pour une transformation graphique.
Vous pouvez également appliquer une transformation de matrice à une SKPoint valeur, un tableau de points, un SKRectou même un seul nombre au sein de votre programme. La SKMatrix structure prend en charge ces opérations avec une collection de méthodes qui commencent par le mot Map, par exemple :
SKPoint transformedPoint = matrix.MapPoint(point);
SKPoint transformedPoint = matrix.MapPoint(x, y);
SKPoint[] transformedPoints = matrix.MapPoints(pointArray);
float transformedValue = matrix.MapRadius(floatValue);
SKRect transformedRect = matrix.MapRect(rect);
Si vous utilisez cette dernière méthode, n’oubliez pas que la SKRect structure n’est pas capable de représenter un rectangle pivoté. La méthode n’est logique que pour une SKMatrix valeur représentant la traduction et la mise à l’échelle.
Expérimentation interactive
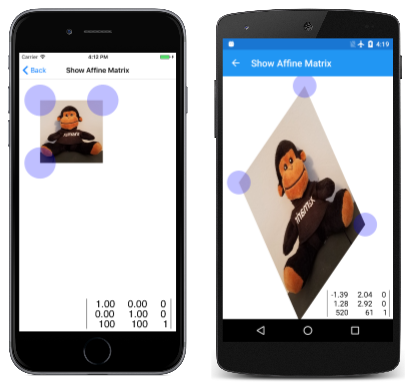
Une façon d’avoir une idée de la transformation affine consiste à déplacer de manière interactive trois coins d’une bitmap autour de l’écran et à voir les résultats de la transformation. Il s’agit de l’idée derrière la page Show Affine Matrix . Cette page nécessite deux autres classes qui sont également utilisées dans d’autres démonstrations :
La TouchPoint classe affiche un cercle translucide qui peut être déplacé autour de l’écran. TouchPoint exige qu’un SKCanvasView ou un élément qui est un parent d’un SKCanvasView élément ait l’élément TouchEffect attaché. Définissez la propriété Capture sur true. Dans le TouchAction gestionnaire d’événements, le programme doit appeler la ProcessTouchEvent méthode dans TouchPoint chaque TouchPoint instance. La méthode retourne true si l’événement tactile a entraîné le déplacement du point tactile. En outre, le PaintSurface gestionnaire doit appeler la Paint méthode dans chaque TouchPoint instance, en lui transmettant l’objet SKCanvas .
TouchPoint illustre une façon courante d’encapsuler un visuel SkiaSharp dans une classe distincte. La classe peut définir des propriétés pour spécifier des caractéristiques du visuel, et une méthode nommée Paint avec un SKCanvas argument peut la restituer.
Propriété Center de TouchPoint indique l’emplacement de l’objet. Cette propriété peut être définie pour initialiser l’emplacement ; la propriété change lorsque l’utilisateur fait glisser le cercle autour du canevas.
La page Show Affine Matrix nécessite également la MatrixDisplay classe. Cette classe affiche les cellules d’un SKMatrix objet. Il a deux méthodes publiques : Measure pour obtenir les dimensions de la matrice rendue et Paint l’afficher. La classe contient une MatrixPaint propriété de type SKPaint qui peut être remplacée pour une autre taille de police ou couleur.
Le fichier ShowAffineMatrixPage.xaml instancie le SKCanvasView fichier et attache un TouchEffect. Le ShowAffineMatrixPage.xaml.cs fichier code-behind crée trois TouchPoint objets, puis les définit sur des positions correspondant à trois coins d’une bitmap qu’il charge à partir d’une ressource incorporée :
public partial class ShowAffineMatrixPage : ContentPage
{
SKMatrix matrix;
SKBitmap bitmap;
SKSize bitmapSize;
TouchPoint[] touchPoints = new TouchPoint[3];
MatrixDisplay matrixDisplay = new MatrixDisplay();
public ShowAffineMatrixPage()
{
InitializeComponent();
string resourceID = "SkiaSharpFormsDemos.Media.SeatedMonkey.jpg";
Assembly assembly = GetType().GetTypeInfo().Assembly;
using (Stream stream = assembly.GetManifestResourceStream(resourceID))
{
bitmap = SKBitmap.Decode(stream);
}
touchPoints[0] = new TouchPoint(100, 100); // upper-left corner
touchPoints[1] = new TouchPoint(bitmap.Width + 100, 100); // upper-right corner
touchPoints[2] = new TouchPoint(100, bitmap.Height + 100); // lower-left corner
bitmapSize = new SKSize(bitmap.Width, bitmap.Height);
matrix = ComputeMatrix(bitmapSize, touchPoints[0].Center,
touchPoints[1].Center,
touchPoints[2].Center);
}
...
}
Une matrice affine est définie de manière unique par trois points. Les trois TouchPoint objets correspondent aux coins supérieur gauche, supérieur droit et inférieur gauche de la bitmap. Étant donné qu’une matrice affine est uniquement capable de transformer un rectangle en parallélisme, le quatrième point est implicite par les trois autres. Le constructeur se termine par un appel à ComputeMatrix, qui calcule les cellules d’un SKMatrix objet à partir de ces trois points.
Le TouchAction gestionnaire appelle la ProcessTouchEvent méthode de chaque TouchPoint. La scale valeur se convertit des Xamarin.Forms coordonnées en pixels :
public partial class ShowAffineMatrixPage : ContentPage
{
...
void OnTouchEffectAction(object sender, TouchActionEventArgs args)
{
bool touchPointMoved = false;
foreach (TouchPoint touchPoint in touchPoints)
{
float scale = canvasView.CanvasSize.Width / (float)canvasView.Width;
SKPoint point = new SKPoint(scale * (float)args.Location.X,
scale * (float)args.Location.Y);
touchPointMoved |= touchPoint.ProcessTouchEvent(args.Id, args.Type, point);
}
if (touchPointMoved)
{
matrix = ComputeMatrix(bitmapSize, touchPoints[0].Center,
touchPoints[1].Center,
touchPoints[2].Center);
canvasView.InvalidateSurface();
}
}
...
}
Si un TouchPoint déplacement a été effectué, la méthode appelle ComputeMatrix à nouveau et invalide la surface.
La ComputeMatrix méthode détermine la matrice implicite par ces trois points. La matrice appelée transforme A un rectangle carré d’un pixel en un parallélisme basé sur les trois points, tandis que la transformation d’échelle appelée S met à l’échelle la bitmap vers un rectangle carré d’un pixel. La matrice composite est S × A:
public partial class ShowAffineMatrixPage : ContentPage
{
...
static SKMatrix ComputeMatrix(SKSize size, SKPoint ptUL, SKPoint ptUR, SKPoint ptLL)
{
// Scale transform
SKMatrix S = SKMatrix.MakeScale(1 / size.Width, 1 / size.Height);
// Affine transform
SKMatrix A = new SKMatrix
{
ScaleX = ptUR.X - ptUL.X,
SkewY = ptUR.Y - ptUL.Y,
SkewX = ptLL.X - ptUL.X,
ScaleY = ptLL.Y - ptUL.Y,
TransX = ptUL.X,
TransY = ptUL.Y,
Persp2 = 1
};
SKMatrix result = SKMatrix.MakeIdentity();
SKMatrix.Concat(ref result, A, S);
return result;
}
...
}
Enfin, la PaintSurface méthode restitue la bitmap en fonction de cette matrice, affiche la matrice en bas de l’écran et affiche les points tactiles aux trois coins de la bitmap :
public partial class ShowAffineMatrixPage : ContentPage
{
...
void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
SKImageInfo info = args.Info;
SKSurface surface = args.Surface;
SKCanvas canvas = surface.Canvas;
canvas.Clear();
// Display the bitmap using the matrix
canvas.Save();
canvas.SetMatrix(matrix);
canvas.DrawBitmap(bitmap, 0, 0);
canvas.Restore();
// Display the matrix in the lower-right corner
SKSize matrixSize = matrixDisplay.Measure(matrix);
matrixDisplay.Paint(canvas, matrix,
new SKPoint(info.Width - matrixSize.Width,
info.Height - matrixSize.Height));
// Display the touchpoints
foreach (TouchPoint touchPoint in touchPoints)
{
touchPoint.Paint(canvas);
}
}
}
L’écran iOS ci-dessous affiche la bitmap lorsque la page est chargée pour la première fois, tandis que les deux autres écrans l’affichent après une manipulation :
Bien qu’il semble que les points tactiles font glisser les angles de la bitmap, c’est seulement une illusion. La matrice calculée à partir des points tactiles transforme l’image bitmap afin que les angles coïncident avec les points tactiles.
Il est plus naturel pour les utilisateurs de déplacer, redimensionner et faire pivoter des bitmaps non pas en faisant glisser les angles, mais en utilisant un ou deux doigts directement sur l’objet pour faire glisser, pincer et faire pivoter. Ceci est abordé dans l’article suivant Manipulation tactile.
La raison de la matrice 3 par 3
On peut s’attendre à ce qu’un système graphique à deux dimensions ne nécessite qu’une matrice de transformation de 2 par 2 :
│ ScaleX SkewY │
| x y | × │ │ = | x' y' |
│ SkewX ScaleY │
Cela fonctionne pour la mise à l’échelle, la rotation et même la rotation, mais elle n’est pas capable des transformations les plus élémentaires, qui est la traduction.
Le problème est que la matrice 2 par 2 représente une transformation linéaire en deux dimensions. Une transformation linéaire conserve certaines opérations arithmétiques de base, mais l’une des implications est qu’une transformation linéaire ne modifie jamais le point (0, 0). Une transformation linéaire rend la traduction impossible.
En trois dimensions, une matrice de transformation linéaire ressemble à ceci :
│ ScaleX SkewYX SkewZX │
| x y z | × │ SkewXY ScaleY SkewZY │ = | x' y' z' |
│ SkewXZ SkewYZ ScaleZ │
La cellule étiquetée SkewXY signifie que la valeur asymétrie de la coordonnée X en fonction des valeurs de Y ; la cellule SkewXZ signifie que la valeur asymétrie de la coordonnée X en fonction des valeurs de Z ; et de valeurs de la même façon pour les autres Skew cellules.
Il est possible de limiter cette matrice de transformation 3D à un plan bidimensionnel en définissant et en définissant SkewZX et SkewZY en 0, et ScaleZ à 1 :
│ ScaleX SkewYX 0 │
| x y z | × │ SkewXY ScaleY 0 │ = | x' y' z' |
│ SkewXZ SkewYZ 1 │
Si les graphiques à deux dimensions sont entièrement dessinés sur le plan dans l’espace 3D où Z est égal à 1, la multiplication de transformation ressemble à ceci :
│ ScaleX SkewYX 0 │
| x y 1 | × │ SkewXY ScaleY 0 │ = | x' y' 1 |
│ SkewXZ SkewYZ 1 │
Tout reste sur le plan bidimensionnel où Z est égal à 1, mais les SkewXZ cellules deviennent SkewYZ effectivement des facteurs de traduction bidimensionnels.
C’est ainsi qu’une transformation linéaire à trois dimensions sert de transformation non linéaire à deux dimensions. (Par analogie, les transformations en graphiques 3D sont basées sur une matrice de 4 par 4.)
La SKMatrix structure dans SkiaSharp définit les propriétés de cette troisième ligne :
│ ScaleX SkewY Persp0 │
| x y 1 | × │ SkewX ScaleY Persp1 │ = | x' y' z` |
│ TransX TransY Persp2 │
Les valeurs non nulles des Persp0Persp1 transformations qui déplacent les objets hors du plan bidimensionnel où Z est égal à 1. Ce qui se passe lorsque ces objets sont déplacés vers ce plan est abordé dans l’article sur les transformations non affines.