Exercice – Estimer les ressources pour un problème réel
L’algorithme de factorisation de Shor est l’un des algorithmes quantiques les plus connus. Il offre une accélération exponentielle par rapport aux algorithmes de factorisation classiques connus.
Le chiffrement classique utilise des approches physiques ou mathématiques, par exemple la difficulté de calcul, pour accomplir une tâche. Le schéma RSA (Rivest-Shamir-Adleman) est un protocole de chiffrement populaire, qui repose sur le principe selon lequel il est difficile de factoriser des nombres premiers à l’aide d’un ordinateur classique.
L’algorithme de Shor implique que des ordinateurs quantiques suffisamment puissants peuvent casser le chiffrement à clé publique. Il est important d’estimer les ressources requises pour l’algorithme de Shor afin d’évaluer la vulnérabilité de ces types de schémas de chiffrement.
Dans l’exercice suivant, vous allez calculer les estimations de ressources pour la factorisation d’un entier de 2 048 bits. Pour cette application, vous calculerez les estimations de ressources physiques directement à partir d’estimations de ressources logiques précalculées. Pour le budget d’erreur toléré, vous utiliserez $\epsilon = 1/3$.
Écrire l’algorithme de Shor
Dans Visual Studio Code, sélectionnez Affichage > Palette de commandes, puis sélectionnez Créer : Notebook Jupyter.
Enregistrez le notebook sous le nom ShorRE.ipynb.
Dans la première cellule, importez le package
qsharp:import qsharpUtilisez l’espace de noms
Microsoft.Quantum.ResourceEstimationpour définir une version mise en cache et optimisée de l’algorithme de factorisation d’entiers de Shor. Ajoutez une nouvelle cellule, puis copiez et collez le code suivant :%%qsharp open Microsoft.Quantum.Arrays; open Microsoft.Quantum.Canon; open Microsoft.Quantum.Convert; open Microsoft.Quantum.Diagnostics; open Microsoft.Quantum.Intrinsic; open Microsoft.Quantum.Math; open Microsoft.Quantum.Measurement; open Microsoft.Quantum.Unstable.Arithmetic; open Microsoft.Quantum.ResourceEstimation; operation RunProgram() : Unit { let bitsize = 31; // When choosing parameters for `EstimateFrequency`, make sure that // generator and modules are not co-prime let _ = EstimateFrequency(11, 2^bitsize - 1, bitsize); } // In this sample we concentrate on costing the `EstimateFrequency` // operation, which is the core quantum operation in Shors algorithm, and // we omit the classical pre- and post-processing. /// # Summary /// Estimates the frequency of a generator /// in the residue ring Z mod `modulus`. /// /// # Input /// ## generator /// The unsigned integer multiplicative order (period) /// of which is being estimated. Must be co-prime to `modulus`. /// ## modulus /// The modulus which defines the residue ring Z mod `modulus` /// in which the multiplicative order of `generator` is being estimated. /// ## bitsize /// Number of bits needed to represent the modulus. /// /// # Output /// The numerator k of dyadic fraction k/2^bitsPrecision /// approximating s/r. operation EstimateFrequency( generator : Int, modulus : Int, bitsize : Int ) : Int { mutable frequencyEstimate = 0; let bitsPrecision = 2 * bitsize + 1; // Allocate qubits for the superposition of eigenstates of // the oracle that is used in period finding. use eigenstateRegister = Qubit[bitsize]; // Initialize eigenstateRegister to 1, which is a superposition of // the eigenstates we are estimating the phases of. // We first interpret the register as encoding an unsigned integer // in little endian encoding. ApplyXorInPlace(1, eigenstateRegister); let oracle = ApplyOrderFindingOracle(generator, modulus, _, _); // Use phase estimation with a semiclassical Fourier transform to // estimate the frequency. use c = Qubit(); for idx in bitsPrecision - 1..-1..0 { within { H(c); } apply { // `BeginEstimateCaching` and `EndEstimateCaching` are the operations // exposed by Azure Quantum Resource Estimator. These will instruct // resource counting such that the if-block will be executed // only once, its resources will be cached, and appended in // every other iteration. if BeginEstimateCaching("ControlledOracle", SingleVariant()) { Controlled oracle([c], (1 <<< idx, eigenstateRegister)); EndEstimateCaching(); } R1Frac(frequencyEstimate, bitsPrecision - 1 - idx, c); } if MResetZ(c) == One { set frequencyEstimate += 1 <<< (bitsPrecision - 1 - idx); } } // Return all the qubits used for oracles eigenstate back to 0 state // using Microsoft.Quantum.Intrinsic.ResetAll. ResetAll(eigenstateRegister); return frequencyEstimate; } /// # Summary /// Interprets `target` as encoding unsigned little-endian integer k /// and performs transformation |k⟩ ↦ |gᵖ⋅k mod N ⟩ where /// p is `power`, g is `generator` and N is `modulus`. /// /// # Input /// ## generator /// The unsigned integer multiplicative order ( period ) /// of which is being estimated. Must be co-prime to `modulus`. /// ## modulus /// The modulus which defines the residue ring Z mod `modulus` /// in which the multiplicative order of `generator` is being estimated. /// ## power /// Power of `generator` by which `target` is multiplied. /// ## target /// Register interpreted as LittleEndian which is multiplied by /// given power of the generator. The multiplication is performed modulo /// `modulus`. internal operation ApplyOrderFindingOracle( generator : Int, modulus : Int, power : Int, target : Qubit[] ) : Unit is Adj + Ctl { // The oracle we use for order finding implements |x⟩ ↦ |x⋅a mod N⟩. We // also use `ExpModI` to compute a by which x must be multiplied. Also // note that we interpret target as unsigned integer in little-endian // encoding by using the `LittleEndian` type. ModularMultiplyByConstant(modulus, ExpModI(generator, power, modulus), target); } /// # Summary /// Performs modular in-place multiplication by a classical constant. /// /// # Description /// Given the classical constants `c` and `modulus`, and an input /// quantum register (as LittleEndian) |𝑦⟩, this operation /// computes `(c*x) % modulus` into |𝑦⟩. /// /// # Input /// ## modulus /// Modulus to use for modular multiplication /// ## c /// Constant by which to multiply |𝑦⟩ /// ## y /// Quantum register of target internal operation ModularMultiplyByConstant(modulus : Int, c : Int, y : Qubit[]) : Unit is Adj + Ctl { use qs = Qubit[Length(y)]; for (idx, yq) in Enumerated(y) { let shiftedC = (c <<< idx) % modulus; Controlled ModularAddConstant([yq], (modulus, shiftedC, qs)); } ApplyToEachCA(SWAP, Zipped(y, qs)); let invC = InverseModI(c, modulus); for (idx, yq) in Enumerated(y) { let shiftedC = (invC <<< idx) % modulus; Controlled ModularAddConstant([yq], (modulus, modulus - shiftedC, qs)); } } /// # Summary /// Performs modular in-place addition of a classical constant into a /// quantum register. /// /// # Description /// Given the classical constants `c` and `modulus`, and an input /// quantum register (as LittleEndian) |𝑦⟩, this operation /// computes `(x+c) % modulus` into |𝑦⟩. /// /// # Input /// ## modulus /// Modulus to use for modular addition /// ## c /// Constant to add to |𝑦⟩ /// ## y /// Quantum register of target internal operation ModularAddConstant(modulus : Int, c : Int, y : Qubit[]) : Unit is Adj + Ctl { body (...) { Controlled ModularAddConstant([], (modulus, c, y)); } controlled (ctrls, ...) { // We apply a custom strategy to control this operation instead of // letting the compiler create the controlled variant for us in which // the `Controlled` functor would be distributed over each operation // in the body. // // Here we can use some scratch memory to save ensure that at most one // control qubit is used for costly operations such as `AddConstant` // and `CompareGreaterThenOrEqualConstant`. if Length(ctrls) >= 2 { use control = Qubit(); within { Controlled X(ctrls, control); } apply { Controlled ModularAddConstant([control], (modulus, c, y)); } } else { use carry = Qubit(); Controlled AddConstant(ctrls, (c, y + [carry])); Controlled Adjoint AddConstant(ctrls, (modulus, y + [carry])); Controlled AddConstant([carry], (modulus, y)); Controlled CompareGreaterThanOrEqualConstant(ctrls, (c, y, carry)); } } } /// # Summary /// Performs in-place addition of a constant into a quantum register. /// /// # Description /// Given a non-empty quantum register |𝑦⟩ of length 𝑛+1 and a positive /// constant 𝑐 < 2ⁿ, computes |𝑦 + c⟩ into |𝑦⟩. /// /// # Input /// ## c /// Constant number to add to |𝑦⟩. /// ## y /// Quantum register of second summand and target; must not be empty. internal operation AddConstant(c : Int, y : Qubit[]) : Unit is Adj + Ctl { // We are using this version instead of the library version that is based // on Fourier angles to show an advantage of sparse simulation in this sample. let n = Length(y); Fact(n > 0, "Bit width must be at least 1"); Fact(c >= 0, "constant must not be negative"); Fact(c < 2 ^ n, $"constant must be smaller than {2L ^ n}"); if c != 0 { // If c has j trailing zeroes than the j least significant bits // of y will not be affected by the addition and can therefore be // ignored by applying the addition only to the other qubits and // shifting c accordingly. let j = NTrailingZeroes(c); use x = Qubit[n - j]; within { ApplyXorInPlace(c >>> j, x); } apply { IncByLE(x, y[j...]); } } } /// # Summary /// Performs greater-than-or-equals comparison to a constant. /// /// # Description /// Toggles output qubit `target` if and only if input register `x` /// is greater than or equal to `c`. /// /// # Input /// ## c /// Constant value for comparison. /// ## x /// Quantum register to compare against. /// ## target /// Target qubit for comparison result. /// /// # Reference /// This construction is described in [Lemma 3, arXiv:2201.10200] internal operation CompareGreaterThanOrEqualConstant(c : Int, x : Qubit[], target : Qubit) : Unit is Adj+Ctl { let bitWidth = Length(x); if c == 0 { X(target); } elif c >= 2 ^ bitWidth { // do nothing } elif c == 2 ^ (bitWidth - 1) { ApplyLowTCNOT(Tail(x), target); } else { // normalize constant let l = NTrailingZeroes(c); let cNormalized = c >>> l; let xNormalized = x[l...]; let bitWidthNormalized = Length(xNormalized); let gates = Rest(IntAsBoolArray(cNormalized, bitWidthNormalized)); use qs = Qubit[bitWidthNormalized - 1]; let cs1 = [Head(xNormalized)] + Most(qs); let cs2 = Rest(xNormalized); within { for i in IndexRange(gates) { (gates[i] ? ApplyAnd | ApplyOr)(cs1[i], cs2[i], qs[i]); } } apply { ApplyLowTCNOT(Tail(qs), target); } } } /// # Summary /// Internal operation used in the implementation of GreaterThanOrEqualConstant. internal operation ApplyOr(control1 : Qubit, control2 : Qubit, target : Qubit) : Unit is Adj { within { ApplyToEachA(X, [control1, control2]); } apply { ApplyAnd(control1, control2, target); X(target); } } internal operation ApplyAnd(control1 : Qubit, control2 : Qubit, target : Qubit) : Unit is Adj { body (...) { CCNOT(control1, control2, target); } adjoint (...) { H(target); if (M(target) == One) { X(target); CZ(control1, control2); } } } /// # Summary /// Returns the number of trailing zeroes of a number /// /// ## Example /// ```qsharp /// let zeroes = NTrailingZeroes(21); // = NTrailingZeroes(0b1101) = 0 /// let zeroes = NTrailingZeroes(20); // = NTrailingZeroes(0b1100) = 2 /// ``` internal function NTrailingZeroes(number : Int) : Int { mutable nZeroes = 0; mutable copy = number; while (copy % 2 == 0) { set nZeroes += 1; set copy /= 2; } return nZeroes; } /// # Summary /// An implementation for `CNOT` that when controlled using a single control uses /// a helper qubit and uses `ApplyAnd` to reduce the T-count to 4 instead of 7. internal operation ApplyLowTCNOT(a : Qubit, b : Qubit) : Unit is Adj+Ctl { body (...) { CNOT(a, b); } adjoint self; controlled (ctls, ...) { // In this application this operation is used in a way that // it is controlled by at most one qubit. Fact(Length(ctls) <= 1, "At most one control line allowed"); if IsEmpty(ctls) { CNOT(a, b); } else { use q = Qubit(); within { ApplyAnd(Head(ctls), a, q); } apply { CNOT(q, b); } } } controlled adjoint self; }
Estimer l’algorithme de Shor
À présent, estimez les ressources physiques pour l’opération RunProgram à l’aide des hypothèses par défaut. Ajoutez une nouvelle cellule, puis copiez et collez le code suivant :
result = qsharp.estimate("RunProgram()")
result
La fonction qsharp.estimate crée un objet de résultat, qui vous permet d’afficher un tableau avec le nombre global de ressources physiques. Vous pouvez examiner les détails des coûts en réduisant les groupes, qui ont plus d’informations.
Par exemple, réduisez le groupe Paramètres des qubits logiques pour voir que la distance de code est de 21, et que le nombre de qubits physiques est de 882.
| Paramètre des qubits logiques | Valeur |
|---|---|
| Schéma QEC | surface_code |
| Distance du code | 21 |
| Qubits physiques | 882 |
| Durée de cycle logique | 8 millisecondes |
| Taux d’erreur des qubits logiques | 3,00E-13 |
| Préfacteur de croisement | 0,03 |
| Seuil de correction d’erreurs | 0,01 |
| Formule de durée de cycle logique | (4 * twoQubitGateTime + 2 * oneQubitMeasurementTime) * codeDistance |
| Formule des qubits physiques | 2 * codeDistance * codeDistance |
Conseil
Pour une version plus compacte de la table de sortie, vous pouvez utiliser result.summary.
Diagramme d’espace
La distribution des qubits physiques utilisés pour l’algorithme et les fabriques T est un facteur qui peut impacter la conception de votre algorithme. Vous pouvez utiliser le package qsharp-widgets pour visualiser cette distribution afin de mieux comprendre les exigences de l’algorithme en matière d’espace nécessaire.
from qsharp_widgets import SpaceChart
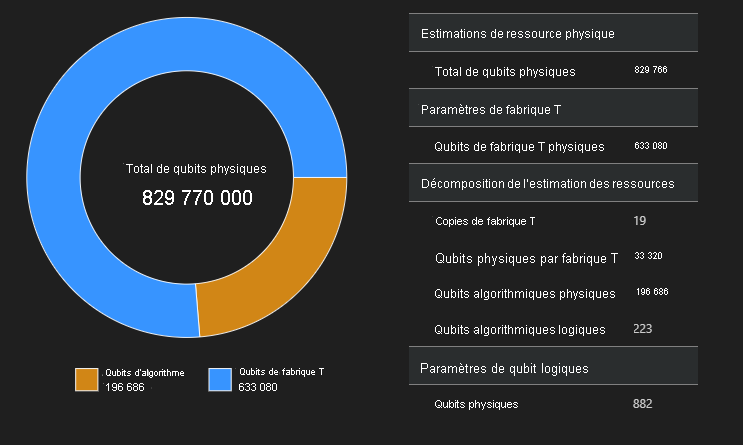
SpaceChart(result)
Dans cet exemple, le nombre de qubits physiques nécessaires à l’exécution de l’algorithme est de 829 766, dont 196 686 sont des qubits d’algorithme et 633080 sont des qubits de fabrique T.
Comparer les estimations de ressources pour différentes technologies de qubit
L’estimateur de ressources Azure Quantum vous permet d’exécuter plusieurs configurations de paramètres cibles, et de comparer les résultats. Cela est utile quand vous souhaitez comparer le coût de différents modèles de qubits, schémas QEC ou budgets d’erreur.
Vous pouvez également construire une liste de paramètres d’estimation à l’aide de l’objet EstimatorParams.
from qsharp.estimator import EstimatorParams, QubitParams, QECScheme, LogicalCounts
labels = ["Gate-based µs, 10⁻³", "Gate-based µs, 10⁻⁴", "Gate-based ns, 10⁻³", "Gate-based ns, 10⁻⁴", "Majorana ns, 10⁻⁴", "Majorana ns, 10⁻⁶"]
params = EstimatorParams(6)
params.error_budget = 0.333
params.items[0].qubit_params.name = QubitParams.GATE_US_E3
params.items[1].qubit_params.name = QubitParams.GATE_US_E4
params.items[2].qubit_params.name = QubitParams.GATE_NS_E3
params.items[3].qubit_params.name = QubitParams.GATE_NS_E4
params.items[4].qubit_params.name = QubitParams.MAJ_NS_E4
params.items[4].qec_scheme.name = QECScheme.FLOQUET_CODE
params.items[5].qubit_params.name = QubitParams.MAJ_NS_E6
params.items[5].qec_scheme.name = QECScheme.FLOQUET_CODE
qsharp.estimate("RunProgram()", params=params).summary_data_frame(labels=labels)
| Modèle de qubit | Qubits logiques | Profondeur logique | États T | Distance du code | Fabriques T | Fraction de fabrique T | Qubits physiques | rQOPS | Temps d’exécution physique |
|---|---|---|---|---|---|---|---|---|---|
| Basé sur une porte, µs, 10⁻³ | 223 3,64 M | 4,70 M | 17 | 13 | 40,54 % | 216,77 k | 21,86 k | 10 heures | |
| Basé sur une porte, µs, 10⁻⁴ | 223 | 3,64 M | 4,70 M | 9 | 14 | 43,17 % | 63,57 k | 41,30 k | 5 heures |
| Basé sur une porte, ns, 10⁻³ | 223 3,64 M | 4,70 M | 17 | 16 | 69,08 % | 416,89 k | 32,79 M | 25 s | |
| Basé sur une porte, ns, 10⁻⁴ | 223 3,64 M | 4,70 M | 9 | 14 | 43,17 % | 63,57 k | 61,94 M | 13 s | |
| Majorana ns, 10⁻⁴ | 223 3,64 M | 4,70 M | 9 | 19 | 82,75 % | 501,48 k | 82,59 M | 10 s | |
| Majorana ns, 10⁻⁶ | 223 3,64 M | 4,70 M | 5 | 13 | 31,47 % | 42,96 k | 148,67 M | 5 secondes |
Extraire des estimations de ressources à partir du nombre de ressources logiques
Si vous connaissez déjà certaines estimations d’une opération, l’estimateur de ressources vous permet d’incorporer les estimations connues dans le coût global du programme pour réduire le temps d’exécution. Vous pouvez utiliser la classe LogicalCounts pour extraire les estimations de ressources logiques à partir de valeurs d’estimation de ressources précalculées.
Sélectionnez Code pour ajouter une nouvelle cellule, puis entrez et exécutez le code suivant :
logical_counts = LogicalCounts({
'numQubits': 12581,
'tCount': 12,
'rotationCount': 12,
'rotationDepth': 12,
'cczCount': 3731607428,
'measurementCount': 1078154040})
logical_counts.estimate(params).summary_data_frame(labels=labels)
| Modèle de qubit | Qubits logiques | Profondeur logique | États T | Distance du code | Fabriques T | Fraction de fabrique T | Qubits physiques | Temps d’exécution physique |
|---|---|---|---|---|---|---|---|---|
| Basé sur une porte, µs, 10⁻³ | 25 481 | 1,2e+10 | 1,5e+10 | 27 | 13 | 0,6 % | 37,38 M | 6 ans |
| Basé sur une porte, µs, 10⁻⁴ | 25 481 | 1,2e+10 | 1,5e+10 | 13 | 14 | 0,8 % | 8,68 M | 3 ans |
| Basé sur une porte, ns, 10⁻³ | 25 481 | 1,2e+10 | 1,5e+10 | 27 | 15 | 1,3 % | 37,65 M | 2 jours |
| Basé sur une porte, ns, 10⁻⁴ | 25 481 | 1,2e+10 | 1,5e+10 | 13 | 18 | 1,2 % | 8,72 M | 18 heures |
| Majorana ns, 10⁻⁴ | 25 481 | 1,2e+10 | 1,5e+10 | 15 | 15 | 1,3 % | 26,11 M | 15 heures |
| Majorana ns, 10⁻⁶ | 25 481 | 1,2e+10 | 1,5e+10 | 7 | 13 | 0,5 % | 6,25 M | 7 heures |
Conclusion
Dans le pire des scénarios, un ordinateur quantique utilisant des qubits µs basés sur des portes (qubits ayant des temps de fonctionnement de l’ordre de la nanoseconde, par exemple les qubits supraconducteurs) et un code QEC de surface aurait besoin de six ans et 37,38 millions de qubits pour factoriser un entier de 2 048 bits à l’aide de l’algorithme de Shor.
Si vous utilisez une autre technologie de qubit, par exemple des qubits d’ions ns basés sur une porte, et le même code de surface, le nombre de qubits ne change pas beaucoup, mais le temps d’exécution peut atteindre deux jours dans le pire des cas et 18 heures dans le meilleur des cas. Si vous changez la technologie de qubit et le code QEC, par exemple en utilisant des qubits basés sur Majorana, la factorisation d’un entier de 2 048 bits avec l’algorithme de Shor peut être effectuée en quelques heures avec un tableau de 6,25 millions de qubits dans le meilleur des cas.
À partir de cette expérience, vous pouvez en conclure que l’utilisation de qubits Majorana et d’un code QEC Floquet est le meilleur choix pour exécuter l’algorithme de Shor et factoriser un entier de 2 048 bits.