Qu’est-ce que l’intrication ?
L’intrication est l’une des principales caractéristiques de la mécanique quantique qui la distingue de la mécanique classique. Mais qu’est-ce que l’intrication au juste ? Comment cela fonctionne-t-il ? Et pourquoi est-elle si importante pour les informations quantiques ?
Dans cette unité, vous allez voir comment définir et décrire l’enchevêtrement quantique, et comprendre pourquoi cette ressource est si puissante pour l’informatique quantique.
Fonctionnement de l’intrication quantique
Imaginez que vous avez deux qubits, $A$ et $B$. Les qubits sont indépendants les uns des autres, ce qui signifie que les informations sur l’état du qubit $A$, quel qu’il soit, appartiennent uniquement au qubit $A$. De même, les informations sur l’état du qubit $B$ appartiennent au qubit $B$. Vous pouvez décrire l’état de chaque qubit. Dans ce cas, les qubits ne sont pas intriqués, car ils ne partagent aucune information.
Imaginez à présent que vous intriquez les qubits (vous apprendrez à le faire plus tard). Si les qubits $A$ et $B$ sont intriqués, les informations sur l’état du qubit $A$ ne sont pas indépendantes de l’état du qubit $B$. En cas d’intrication, les informations sont partagées entre les deux qubits, et il n’est pas possible de déduire l’état du qubit $A$ ou $B$. Vous pouvez uniquement décrire l’état du système global, et non celui de chaque qubit.
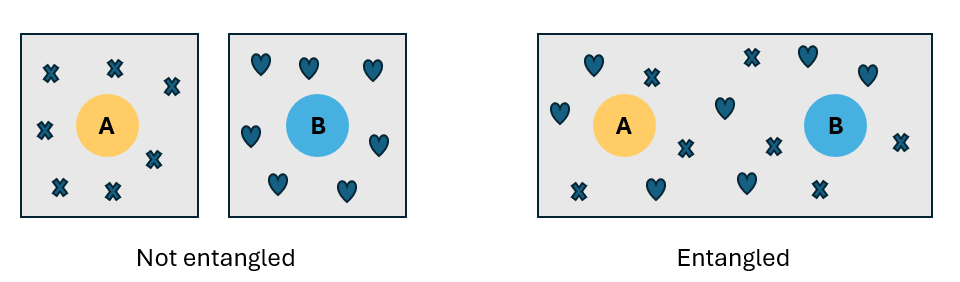
L’intrication est une corrélation quantique entre deux particules ou plus. Si deux particules sont intriquées, elles ne peuvent pas être décrites de manière indépendante, mais seulement en tant que système dans son ensemble.
Description de l’intrication quantique
Imaginez deux qubits, soit $A$ et $B$, de sorte que l’état du système global $\ket{\phi}$ soit :
$$\ket{\phi}=\frac1{\sqrt2}(\ket{0_A 0_B}+ \ket{1_A 1_B})$$
Remarque
En notation Dirac, $\ket{0_A 0_B}=|0\rangle_\text{A}|0\rangle_\text{B}$. La première position correspond au premier qubit et la seconde position au deuxième qubit.
Le système global $\ket{\phi}$ est dans une superposition des états $|00\rangle$ et $|11\rangle$. Si vous mesurez les deux qubits, seuls deux résultats sont possibles : $\ket{{00}$ et $\ket{{11}$, et chacun a la même probabilité de $\frac{1}{{2}$.
Quel est toutefois l’état individuel du qubit $A$ ? Et celui du qubit $B$ ? Si vous essayez de décrire l’état du qubit $A$ sans tenir compte de celui du qubit $B$, vous n’y parviendriez pas. Les sous-systèmes $A$ et $B$ sont intriqués, ce qui signifie qu’ils sont corrélés et ne peuvent pas être décrits de manière indépendante.
Conseil
Si vous connaissez l’algèbre et la notation Dirac, un bon exercice consiste à essayer de modifier l’état $\ket{\phi}$ pour obtenir quelque chose tel que l’état du qubit $A$ multiplié par l’état du qubit $B$. Si vous essayez d’étendre la parenthèse, d’obtenir le facteur commun, etc., vous constaterez que cela n’est pas possible.
L’état quantique $\ket{\phi}$ est un état intriqué spécial, appelé état de Bell. Il existe quatre états de Bell.
$$\ket{\phi^{+}}=\frac1{\sqrt2}\ket{{00} + \frac1{\sqrt2}\ket{{11}$$$$\ket{\phi^{-}}=\frac1{\sqrt2}\ket{00} - \frac1{\sqrt2}\ket{11}$$$$\ket{\psi^{+}}=\frac1{\sqrt2}\ket{{01} + \frac1{\sqrt2}\ket{{10}$$$$\ket{\psi^{-}}=\frac1{\sqrt2}\ket{01} - \frac1{\sqrt2}\ket{10}$$
Utilisation de l’intrication en tant que ressource
À ce stade, vous vous demandez peut-être en quoi l’intrication est-elle si particulière.
Lorsque deux particules sont intriquées, les sous-systèmes sont corrélés et ne peuvent pas être décrits de manière indépendante. Et voici la partie intéressante : les résultats de mesure sont également corrélés. Autrement dit, toute opération effectuée sur l’état d’un qubit dans une paire intriquée affecte également l’état de l’autre qubit.
Prenons l’exemple de l’état $\ket{\phi^{+}}$,
$$\ket{\phi^{+}}=\frac1{\sqrt2}\ket{{00} + \frac1{\sqrt2}\ket{{11}$$
Si vous mesurez les deux qubits, vous obtenez $|00\rangle$ ou $|11\rangle$ selon une probabilité égale. La probabilité d’obtenir $|01\rangle$ et $|10\rangle$ est nulle.
Mais que se passe-t-il si vous ne mesurez qu’un seul qubit ?
Si vous mesurez uniquement le qubit $A$ et que vous obtenez l’état $|0\rangle$, cela signifie que le système global se réduit à l’état $\ket{00}$. Il s’agit du seul résultat possible, car la probabilité de mesurer $|01\rangle$ est nulle.
Par conséquent, sans mesurer le qubit $B$, vous pouvez savoir avec certitude que le second qubit est également dans l’état $|0\rangle$. Les résultats de la mesure sont corrélés, car les qubits sont intriqués.
L’intrication peut exister entre deux particules même une grande distance les sépare. Cette corrélation est plus forte que n’importe quelle corrélation classique. Il s’agit d’une ressource essentielle pour les tâches de traitement des informations quantiques telles que la téléportation quantique, le chiffrement quantique et l’informatique quantique.