Créer un enchevêtrement quantique avec Q#

7 minutes

Dans l’unité précédente, vous avez découvert le concept d’intrication de quantum et les états de Bell.

Créons maintenant l’intrication de quantum à l'aide de Q# et d’Azure Quantum Development Kit. Pour créer l’intrication, il faut appliquer deux opérations quantum : la porte de Hadamard et la porte CNOT (Controlled-NOT).

Opération Controlled-NOT (CNOT)

Lorsque deux qubits sont enchevêtrés, l’état de l’un dépend de l’état de l’autre. Par conséquent, pour enchevêtrer deux qubits, vous avez besoin d’opérations qui agissent sur les deux qubits en même temps. Il s’agit là d’une opération multiqubit.

Pour créer un enchevêtrement quantique, vous avez besoin de l’opération multiqubit CNOT, qui signifie Controlled-NOT. Cette opération prend deux qubits comme entrée. L’un fait office de qubit de contrôle et l’autre est le qubit target . L’opération CNOT inverse l’état du second qubit (le qubit target) si, et seulement si, l’état du premier qubit (le qubit de contrôle) est $|1\rangle$.

Entrée	Sortie
$\ket{00}$	$\ket{00}$
$\ket{01}$	$\ket{01}$
$\ket{10}$	$\ket{11}$
$\ket{11}$	$\ket{10}$

Dans Q#, l’opération CNOT agit sur un tableau de deux qubits et retourne le deuxième qubit si le premier qubit est One.

Enchevêtrement avec une opération CNOT

En appliquant Hadamard, H, l’opération et le Controlled-NOT, CNOT, l’opération, pouvez transformer deux qubits dans l’état $|00\rangle$ à l’état Cloche $\ket{\phi^+}=\frac1{\sqrt2}(|00\rangle+|11\rangle)$.

Voici son fonctionnement :

Prenez deux qubits dans l’état $|00\rangle$. Le premier qubit est le qubit de contrôle et le second qubit est le qubit target.
Préparez un état de superposition dans le qubit de contrôle en appliquant $H$.

$$H |0_c\rangle=\frac{1}{\sqrt{{2}}(|0_c\rangle+|1_c\rangle)$$

Remarque

Les indices ${}_c$ et ${}_t$ spécifient le contrôle et les qubits target.
Appliquez l’opérateur $CNOT$ au qubit de contrôle qui se trouve dans un état de superposition, ainsi qu’au qubit target qui se trouve dans l’état $|0_t\rangle$.

$$ CNOT \frac{1}{\sqrt{2}}(\ket{0_c}+\ket{1_c})\ket{0}_t = CNOT \frac{1}{\sqrt2}(\ket{0_c 0_t}+|\ket{1_c 0_t})=$$$$=\frac{{1}{\sqrt2}(CNOT \ket{0_c 0_t} + CNOT \ket{1_c 0_t})=$$$$=\frac{1}{\sqrt2}(\ket{0_c 0_t}+\ket{1_c 1_t})$$

Créer un fichier Q#

Ouvrez Visual Studio Code.
Sélectionnez Fichier > Nouveau fichier texte, puis enregistrez celui-ci sous le nom Main.qs.
Sélectionnez Afficher -> Palette de commandes et tapez Q# : Définir le profil QIR target Azure Quantum. Appuyez sur Entrée.
Sélectionnez Q# : Sans restriction.

Créer et mesurer l’état Cloche $\ket{\phi^+}$

Commençons par créer l’état Bell $\ket{\phi^+}=\frac1{\sqrt2}(|00\rangle+|11\rangle)$.

Créer l’état Cloche $\ket{\phi^+}$ dans Q#

Tout d’abord, vous devez importer l’espace de noms Microsoft.Quantum.Diagnostics à partir de la bibliothèque Standard, qui contient la fonction DumpMachine. Cette fonction affiche l’état actuel des qubits. Copiez et collez le code Q# suivant dans le fichier Main.qs.
```
import Microsoft.Quantum.Diagnostics.*; // Aka Std.Diagnostics.*;
```
Conseil

Vous pouvez également importer la bibliothèque Standard en remplaçant Microsoft.Quantum par Std. Par exemple, import Std.Diagnostics.* équivaut à import Microsoft.Quantum.Diagnostics.*.

Créez l’opération Main qui retourne deux valeurs de type Result, qui sont les résultats de mesure des qubits.

import Microsoft.Quantum.Diagnostics.*; // Aka Std.Diagnostics.*;

operation Main() : (Result, Result) {
    // Your code goes here
}

À l’intérieur de l’opération Main, vous allouez deux qubits, q1 et q2, qui seront enchevêtrés.

import Microsoft.Quantum.Diagnostics.*; // Aka Std.Diagnostics.*;

operation Main() : (Result, Result) {
    use (q1, q2) = (Qubit(), Qubit());
}

Appliquez la porte Hadamard, H, au premier qubit, q1, pour la placer dans un état de superposition. Ensuite, les deux qubits sont enchevêtrés en utilisant l’opération CNOT.

import Microsoft.Quantum.Diagnostics.*; // Aka Std.Diagnostics.*;

operation Main() : (Result, Result) {
    use (q1, q2) = (Qubit(), Qubit());

    H(q1);
    CNOT(q1, q2);
}

Utilisez la fonction DumpMachine pour afficher l’état actuel des qubits. Cette fonction n’est pas similaire à la mesure des qubits.

import Microsoft.Quantum.Diagnostics.*; // Aka Std.Diagnostics.*;

operation Main() : (Result, Result) {
    use (q1, q2) = (Qubit(), Qubit());

    H(q1);
    CNOT(q1, q2);

    DumpMachine();
}

Mesurez les qubits à l’aide de l’opération M et stockez les résultats dans m1 et m2. Ensuite, utilisez l’opération Reset pour réinitialiser les qubits. Dans Q#, vous devez toujours réinitialiser les qubits à l’état $|0\rangle$.

import Microsoft.Quantum.Diagnostics.*; // Aka Std.Diagnostics.*;

operation Main() : (Result, Result) {

    use (q1, q2) = (Qubit(), Qubit());

    H(q1);
    CNOT(q1, q2);
    DumpMachine();

    let (m1, m2) = (M(q1), M(q2));
    Reset(q1);
    Reset(q2);

}

Enfin, retournez les résultats de mesure des qubits avec l’instruction return. Votre fichier Main.qs doit ressembler à ceci :

import Microsoft.Quantum.Diagnostics.*; // Aka Std.Diagnostics.*;

operation Main() : (Result, Result) {
    use (q1, q2) = (Qubit(), Qubit());

    H(q1);
    CNOT(q1, q2);

    DumpMachine();

    let (m1, m2) = (M(q1), M(q2));
    Reset(q1);
    Reset(q2);

    return (m1, m2);
}

Exécuter le programme

Pour exécuter votre programme sur le simulateur intégré, cliquez sur Exécuter au-dessus de l’opération Main ou appuyez sur Ctrl+F5. Votre sortie s’affiche dans la console de débogage.
Étant donné que les résultats de mesure sont corrélés, à la fin du programme, vous obtenez un résultat de (Zero, Zero) ou de (One, One) avec une probabilité égale.
Vous pouvez visualiser le diagramme de circuit en cliquant sur Circuit dans la liste des commandes sur l’opération Main. Le diagramme du circuit montre la porte Hadamard appliquée au premier qubit et la porte CNOT appliquée aux deux qubits.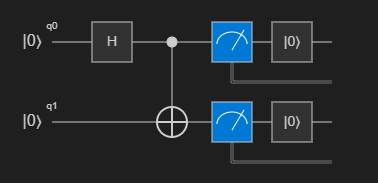

Créer et mesurer l’état Cloche $\ket{\phi^-}$

Pour créer d’autres états Bell, vous devez appliquer d’autres opérations Pauli $X$ et $Z$ aux qubits.

Par exemple, pour créer l’état Bell $\ket{\phi^-}=\frac1{\sqrt2}(|00\rangle-|11\rangle)$, vous pouvez appliquer l’opération Pauli $Z$ au qubit de contrôle après l’application de la porte Hadamard. L’opération $Z$ retourne l’état $\ket{+}$ à $\ket{-}$.

Remarque

Les états $\frac{{1}{\sqrt{2}}(|0\rangle+|1\rangle)$ et $\frac{1}{\sqrt{{2}}(|0\rangle -|1\rangle)$ sont également appelés $\ket{+}$ et $\ket{{-}$, respectivement.

Voici son fonctionnement :

Prenez deux qubits dans l’état $|00\rangle$.
Préparez un état de superposition dans le qubit de contrôle en appliquant $H$.

$$H |0_c\rangle=\frac{{1}{\sqrt{2}}(|0_c\rangle+|1_c\rangle) =\ket{+}_c$$
Appliquez l’opération $Z$ au qubit de contrôle.

$$Z \frac{{1}{\sqrt{{2}}(|0_c\rangle+|1_c\rangle)=\frac{1}{\sqrt{{2}}(|0_c\rangle-|1_c\rangle)=\ket{{-}_c$$
Appliquez l’opérateur $CNOT$ au qubit de contrôle et au qubit target qui se trouve dans l’état $|0_t\rangle$.

$$ CNOT \frac{1}{\sqrt{2}}(\ket{0_c}-\ket{1_c})\ket{0}_t = CNOT \frac{1}{\sqrt2}(\ket{0_c 0_t}-|\ket{1_c 0_t})=$$$$=\frac{{1}{\sqrt2}(CNOT \ket{0_c 0_t} - CNOT \ket{1_c 0_t})=$$$$=\frac{1}{\sqrt2}(\ket{0_c 0_t}-\ket{1_c 1_t})$$

Créer l’état Cloche $\ket{\phi^-}$ dans Q#

Modifiez le code Q# pour créer l’état Bell $\ket{\phi^-}$. Votre fichier Main.qs doit ressembler à ceci :

import Microsoft.Quantum.Diagnostics.*; // Aka Std.Diagnostics.*;

operation Main() : (Result, Result) {
    use (q1, q2) = (Qubit(), Qubit());

    H(q1);
    Z(q1); // Apply the Pauli Z operation to the control qubit
    CNOT(q1, q2);

    DumpMachine();

    let (m1, m2) = (M(q1), M(q2));
    Reset(q1);
    Reset(q2);

    return (m1, m2);
}

Pour exécuter votre programme sur le simulateur intégré, cliquez sur Exécuter au-dessus de l’opération Main ou appuyez sur Ctrl+F5. Votre sortie s’affiche dans la console de débogage.
Vous pouvez visualiser le diagramme de circuit en cliquant sur Circuit dans la liste des commandes sur l’opération Main. Le diagramme de circuit montre la porte Hadamard appliquée au premier qubit, la porte Pauli $Z$ appliquée au premier qubit et la porte CNOT appliquée aux deux qubits.

Exercice bonus : Créer les états Bell $\ket{\psi^+}$ et $\ket{\psi^-}$

De même, les états Bell $\ket{\psi^+}$ et $\ket{\psi^-}$ peuvent être créés en appliquant les opérations Pauli $X$ et $Z$ aux qubits.

L’état Bell $\ket{\psi^+}=\frac1{\sqrt2}(|01\rangle+|10\rangle)$ peut être créé en appliquant l’opération Pauli $X$ au qubit target après l’application de la porte Hadamard.
L’état Bell $\ket{\psi^-}=\frac1{\sqrt2}(|01\rangle-|10\rangle)$ peut être créé en appliquant le Pauli $Z$ au qubit de contrôle et le Pauli $X$ au qubit target après l’application de la porte Hadamard.

Modifiez le programme Main.qs pour créer les états Cloche $\ket{\psi^+}$ et $\ket{\psi^-}$.