Comment utiliser l’intrication pour envoyer des informations ?
Dans les unités précédentes, nous avons vu que l’intrication quantum peut être une excellente ressource pour la communication quantum. Dans cette unité, vous verrez l’une des applications les plus courantes de l’intrication à savoir : le protocole de téléportation quantum.
En matière de téléportation, l’intrication est utilisée pour transférer l’état d’un qubit d’un emplacement à un autre. L’état du qubit est transféré vers un autre qubit, mais le qubit lui-même n’est pas déplacé physiquement. Il s’agit d’un point important à retenir ! Les informations de l’état du qubit sont transférées vers un autre qubit utilisé comme conteneur pour y écrire les informations du qubit de message.
Le protocole de téléportation utilise une combinaison d’intrication et de communication classique. La communication classique est importante, car le protocole de téléportation exige que l’émetteur communique les résultats de ses mesures au récepteur. Nous ne pouvons dès lors pas utiliser la téléportation pour envoyer des informations à une vitesse supérieure à celle de la lumière. La communication classique entre l’émetteur et le récepteur est limitée par la vitesse de la lumière.
Passons en revue le protocole de téléportation quantique.
Protocole de téléportation quantique
Alice et Bob travaillent ensemble dans la même entreprise. Alice est située à Seattle et Bob à Los Angeles. Ils collaborent sur un projet qui les oblige à partager des informations quantiques. Ils décident d’utiliser la téléportation quantique pour s’échanger des informations quantiques.
Configuration initiale
Alice et Bob ont chacun un qubit qui fait partie d’une paire intriquée qui a été préparée précédemment. La paire intriquée est un état de Bell, qui correspond à l’état
$$\ket{\phi}=\frac1{\sqrt2}(\ket{0_A 0_B} + \ket{1_A 1_B})$$
Alice a un qubit supplémentaire, appelé « qubit de message », qu’elle souhaite envoyer à Bob. Le qubit de message est dans un état inconnu qu’Alice veut téléporter à Bob. L’état du qubit de message est
$$\ket{m}=\alpha\ket{{0}_m + \beta\ket{{1}_m,$$
où $\alpha$ et $\beta$ correspondent à des nombres complexes.
L’état global des trois qubits d’Alice et de Bob est
$$\ket{\text{Global}}= (\alpha\ket{{0}_m + \beta\ket{1}_m) \otimes\frac1{\sqrt2}(\ket{0_A 0_B}+ \ket{1_A 1_B}) $$
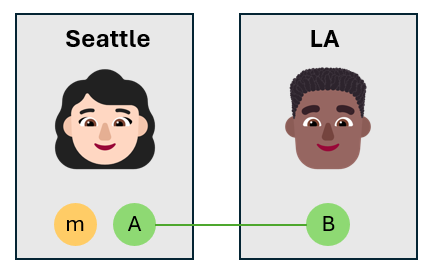
Alice intrique le qubit de message à son propre qubit
Alice utilise le qubit de message et l’intrique à son propre qubit $A$ à l’aide d’une porte CNOT. Le qubit de message est le qubit de contrôle et le qubit d’Alice est le qubit target. Cette situation crée un état intriqué de trois qubits.
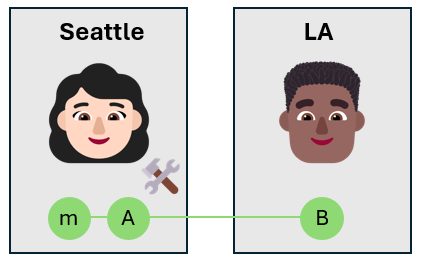
Le qubit de message est dans l’état inconnu $\alpha\ket{0}_m + \beta\ket{1}_m$. Par conséquent, après l’application de la porte CNOT, les qubits d’Alice sont dans une superposition des quatre états de Bell. L’état global des trois qubits est
$$\ket{\text{Global}}=\frac1{{2}\ket{\phi^+}_\text{mA} (\alpha\ket{{0}_B + \beta\ket{{1}_B) + $$
$$ + \frac1{{2}\ket{\phi^-}_\text{mA} (\alpha\ket{0}_B - \beta\ket{1}_B) +$$
$$ + \frac1{{2}\ket{\psi^+}_\text{mA}(\alpha\ket{1}_B + \beta\ket{0}_B) + $$
$$ + \frac1{{2}\ket{\psi^-}_\text{mA} (\alpha\ket{1}_B- \beta\ket{0}_B)$$
L’état global des qubits d’Alice et de Bob est une superposition de quatre états possibles.
Conseil
Un bon exercice consiste à vérifier que l’état global des trois qubits est celui indiqué ci-dessus. Pour ce faire, appliquez la porte CNOT au qubit de message et au qubit d’Alice, puis développez l’état des trois qubits.
Alice mesure les qubits
Alice mesure ensuite le qubit de message et son propre qubit. Elle ne mesure pas les qubits dans la base $Z$ comme d’habitude, mais elle choisit la base de Bell. La base de Bell est constituée des quatre états de Bell, à savoir $\lbrace \ket{\phi^+}, \ket{\phi^-}, \ket{\psi^+}, \ket{\psi^-} \rbrace$.
En mesurant le qubit de message et son propre qubit dans la base de Bell, Alice projette ses qubits dans l’un des quatre états de Bell. Étant donné que les trois qubits sont intriqués, les résultats de mesure sont corrélés. Quand Alice mesure ses qubits, le qubit de Bob est également projeté dans l’état corrélé.
Par exemple, si Alice mesure ses qubits et observe l’état $\ket{\phi^-}$, le qubit de Bob est projeté dans l’état $\alpha\ket{0}_B - \beta\ket{1}_B$.
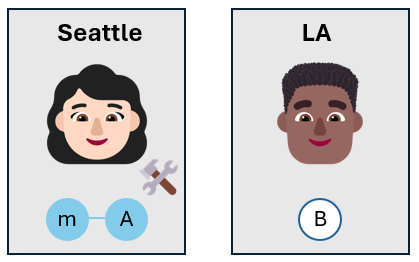
Alice appelle Bob
Alice appelle Bob pour lui communiquer les résultats de ses mesures. Elle utilise un canal de communication classique, comme un appel téléphonique ou un SMS.
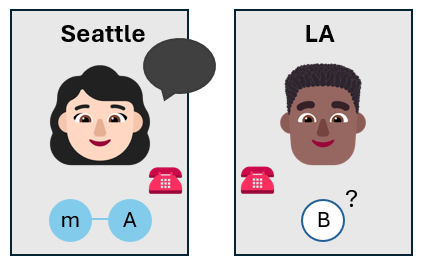
Bob connaît à présent l’état de son propre qubit, sans avoir à le mesurer. L’état du qubit de Bob peut être différent de celui du qubit de message qu’Alice souhaitait téléporter, mais il en est proche.
Bob applique une opération quantique
Ensuite, Bob peut récupérer l’état d’origine du qubit de message en appliquant une opération quantique spécifique à son qubit. L’opération que Bob effectue dépend de ce qu’Alice lui a dit par téléphone.
L’opération qu’il exécute peut être une porte Pauli $X$, une porte Pauli $Z$, les deux ou aucune.
Par exemple, si le résultat de la mesure d’Alice est $\ket{\phi^-}$, Bob sait que son qubit est dans l’état $(\alpha\ket{0}_B - \beta\ket{1}_B)$. Il doit uniquement appliquer une porte Pauli Z pour récupérer l’état d’origine du qubit de message.
| Alice mesure | Bob applique |
|---|---|
| $\ket{\phi^+}$ | Pas d’opération |
| $\ket{\phi^-}$ | Porte Pauli Z |
| $\ket{\psi^+}$ | Porte Pauli X |
| $\ket{\psi^-}$ | Porte Pauli X suivie d’une porte Pauli Z |
Cette opération finale téléporte l’état du qubit de message vers le qubit de Bob. Mission accomplie !
Important
Appliquer une opération à un qubit n’est pas la même que le mesurer. Quand Bob applique l’opération, il ne mesure pas son qubit. Il applique une opération quantique qui modifie l’état du qubit, mais ne le réduit pas.