Qu’est-ce que la superposition dans l’informatique quantique ?
Si le chat de l’unité précédente était un chat quantique, l’état du chat quantique et du système de boîte serait le même : la somme des six positions différentes du chat quantique par rapport à la boîte, pondérée par la probabilité de trouver le chat quantique dans cette position. La seule différence est que le chat classique peut être dans une (et une seule) des six positions possibles alors que le chat quantique peut être dans les six positions en même temps !
Dans le monde classique, les objets ne peuvent être qu’à un seul état à la fois. Toutefois, dans le monde quantique, les particules quantiques peuvent se trouver dans plusieurs états en même temps. Ce phénomène s’appelle la superposition.
Dans l’informatique quantique, personne n’utilise des chats quantiques – malheureusement – mais des qubits. Le mot « qubit » signifie « bit quantique ». Tout comme dans l’informatique classique, où l’unité de base des informations est le bit, dans l’informatique quantique, l’unité de base des informations est le qubit. Tout comme le bit peut prendre deux valeurs possibles, 0 et 1, un qubit est toute particule quantique qui peut se trouver dans deux états possibles. Par exemple, un qubit peut être un photon, qui peut être polarisé dans deux directions, ou un électron, qui peut se trouver dans deux niveaux d’énergie.
Comment faire pour représenter la superposition dans un qubit ? Quelle est la probabilité de trouver un qubit dans un état particulier ?
Comment faire pour représenter la superposition dans un qubit ?
Un qubit est une particule quantique qui a deux positions, ou états, possibles. De manière analogue aux bits classiques, les états quantiques d’un qubit sont également appelés $0$ et $1$. Un qubit peut être à l’état $0$, à l’état $1$, et dans n’importe quelle superposition des deux états. Comment représenter cette superposition ?
Imaginez que vous dessinez un cercle et un axe vertical et horizontal de sorte que le point central soit le centre du cercle. L’état $0$ est placé au point supérieur de l’axe vertical, et l’état $1$ est au point inférieur.
Comment faire pour décrire cette représentation ? Vous pourriez dire que l’état $0$ est une flèche, ou un vecteur, pointant vers le haut, et que l’état $1$ est un vecteur pointant vers le bas. Par conséquent, un bit classique serait un vecteur pointant vers le haut ou vers le bas, mais jamais dans une autre direction.
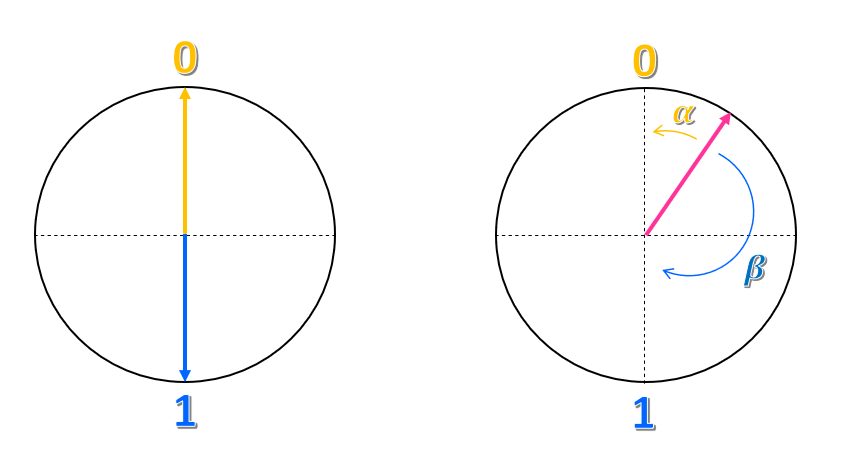
Qu’en est-il d’un autre point du cercle ? Comment faire pour représenter cet état ? Tout comme les coordonnées dans un plan, vous pourriez essayer de le représenter comme une combinaison des deux états $0$ et $1$. Par exemple, vous pourriez prendre la proximité du vecteur par rapport à l’état $0$ et appeler cet angle $\alpha$, et sa proximité par rapport à l’état $1$ et appeler cet angle $\beta$. Nous pourrions représenter l’état comme $\alpha 0 + \beta 1 $. Ainsi, l’état est une superposition des états $0$ et $1$.
Tout comme avec l’exemple du chat et de la boîte, l’état global d’un qubit est la somme des états individuels, $0$ et $1$, pondérée par la probabilité de trouver le qubit dans cet état, $\alpha$ et $\beta $.
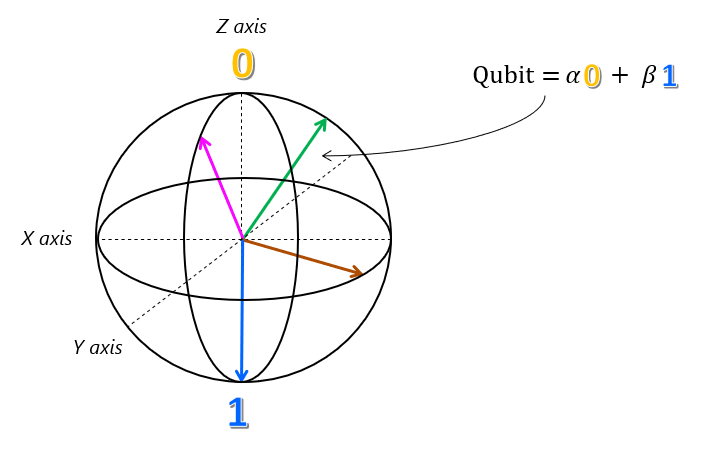
Cette représentation d’un qubit est précisément juste, et elle est connue sous le nom de sphère de Bloch.
Conseil
La sphère de Bloch est un outil puissant, car les opérations que nous pouvons effectuer sur un qubit peuvent être représentées sous forme de rotations autour de l’un des axes cardinaux. Envisager un calcul quantique comme séquence de rotations permet un excellent raisonnement intuitif, qu’il est cependant difficile d’utiliser pour concevoir et décrire des algorithmes. Q# atténue ce problème en fournissant un langage permettant de décrire ces rotations.
Quelle est la probabilité de trouver un qubit dans un état ?
Comme avec l’exemple du chat et de la boîte de l’unité précédente, l’état global d’un qubit est la somme des états individuels, $0$ et $1$, pondérée par la probabilité de trouver le qubit dans cet état, $\alpha$ et $\beta $. Les nombres $\alpha$ et $\beta$ représentent respectivement la « proximité » de l’état qubit des états $0$ et $1$. $\alpha$ et $\beta$ correspondent-ils donc à la probabilité de trouver le qubit à l’état $0$ ou $1$ ? Pas forcément.
Les nombres $\alpha$ et $\beta$ sont des amplitudes de probabilité pour chaque état. Leurs valeurs absolues, par exemple $|\alpha|^2$, donnent les probabilités correspondantes. Par exemple, la probabilité d’observer l’état $0$ est $|\alpha|^2$, et la probabilité d’observer l’état $1$ est $|\beta|^2$.
Les nombres $\alpha$ et $\beta$ peuvent être positifs, négatifs ou même complexes. Toutefois, dans une superposition quantique valide, la somme de toutes les probabilités doit être égale à 1 : $|\alpha|^2+|\beta|^2=1$. Cette contrainte est appelée condition de normalisation. La condition de normalisation revient à générer toujours un résultat lorsque vous mesurez, de sorte que les probabilités de mesure de chaque résultat possible doivent être additionnées pour obtenir la valeur 1.