Optimiser les modèles en utilisant la descente de gradient

  • 6 minutes

Nous avons vu comment les fonctions de coût évaluent les performances des modèles à l’aide de données. L’optimiseur est la dernière pièce du puzzle.

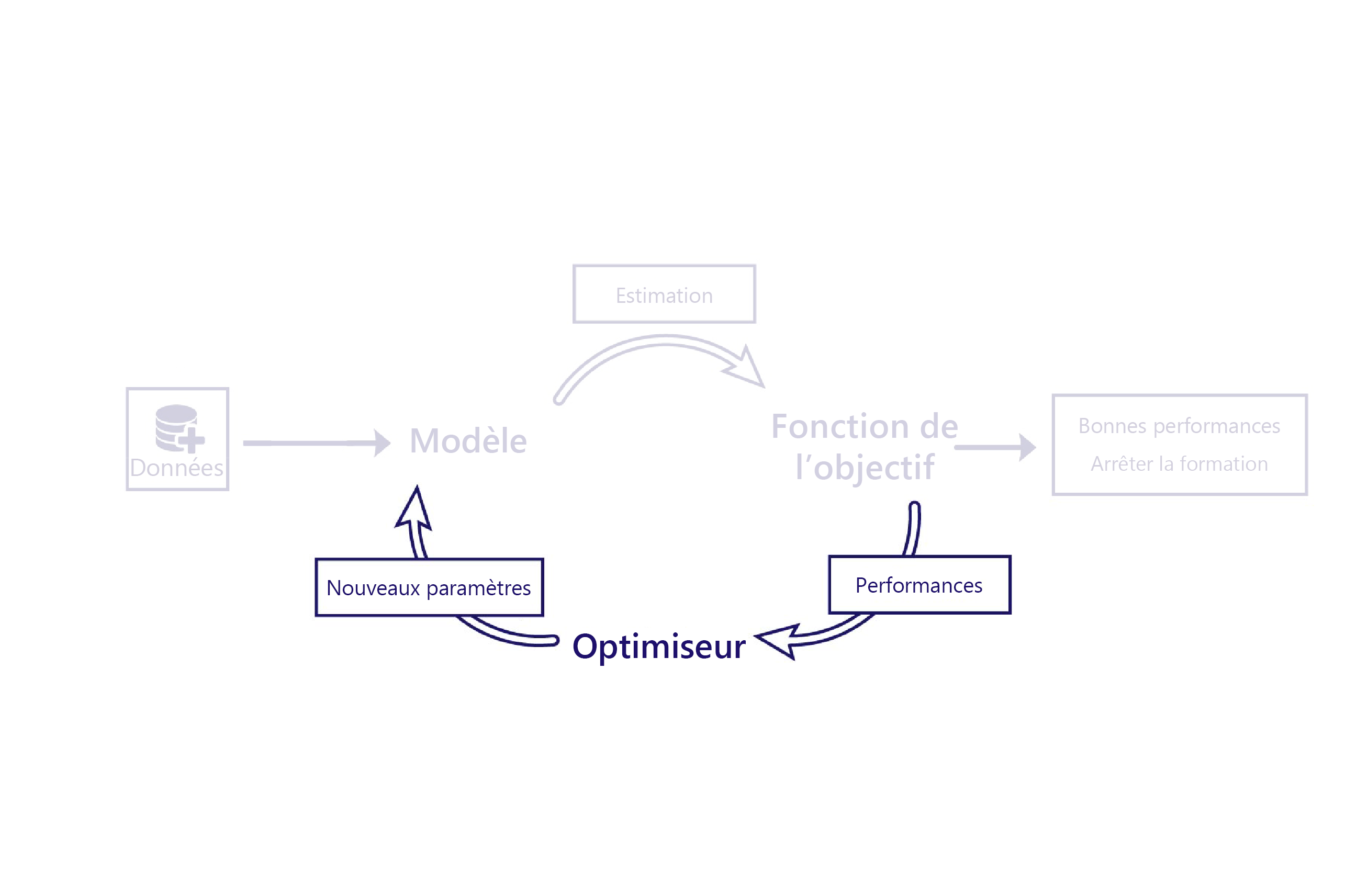
Le rôle de l’optimiseur est de modifier le modèle de façon à améliorer ses performances. Cette modification est effectuée en inspectant les sorties et le coût du modèle, et en suggérant de nouveaux paramètres pour le modèle.

Par exemple, dans notre scénario d’élevage, notre modèle linéaire a deux paramètres : le point d’intersection de la ligne et la pente de la ligne. Si le point d’intersection de la ligne est mauvais, le modèle sous-évalue ou surévalue les températures moyennes. Si la pente est mal définie, le modèle ne montre pas correctement l’évolution des températures depuis les années 1950. L’optimiseur modifie ces deux paramètres pour qu’ils fassent un travail optimal dans la modélisation des températures au fil du temps.

Diagramme montrant la partie optimiseur du cycle de vie du machine learning.

Descente de gradient

L’algorithme d’optimisation le plus courant aujourd’hui est la descente de gradient. Il existe plusieurs variantes de cet algorithme, mais elles utilisent toutes les mêmes concepts de base.

La descente de gradient utilise des calculs pour estimer dans quelle mesure le changement de chaque paramètre changera le coût. Par exemple, elle peut prédire qu’augmenter la valeur d’un paramètre va réduire le coût.

La descente de gradient s’appelle ainsi parce qu’elle calcule le gradient (la pente) de la relation entre chaque paramètre du modèle et le coût. Les paramètres sont ensuite modifiés pour incliner cette pente vers le bas.

Cet algorithme est simple et puissant ; il n’est cependant pas garanti qu’il va trouver les paramètres optimaux du modèle qui vont réduire le coût au minimum. Les deux principales sources d’erreur sont les minima locaux et l’instabilité.

Minimum local

Notre exemple précédent semble faire du bon travail, en supposant que le coût continue d’augmenter quand le paramètre est inférieur à zéro ou supérieur à 10 :

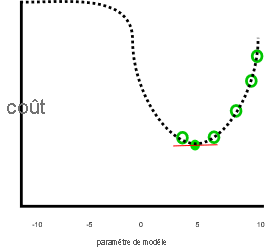
Tracé du coût par rapport au paramètre du modèle, avec un minimum pour le coût quand le paramètre du modèle est égal à cinq.

Ce travail n’est pas aussi bon si des paramètres inférieurs à zéro ou supérieurs à 10 entraînent des coûts inférieurs, comme dans cette image :

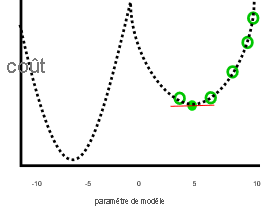
Tracé du coût par rapport au paramètre du modèle, avec un minimum local pour le coût quand le paramètre du modèle est égal à cinq, mais avec un coût inférieur quand le paramètre du modèle est égal à moins six.

Dans le graphique précédent, une valeur de paramètre égale à moins sept est une meilleure solution que cinq, car son coût est moindre. La descente de gradient ne connaît pas à l’avance la relation complète entre chaque paramètre et le coût (représenté par la ligne en pointillés). Elle a donc tendance à rechercher le minimum local : les estimations de paramètre qui ne sont pas la meilleure solution, mais pour lesquelles le gradient est égal à zéro.

Instabilité

Un problème connexe est que la descente de gradient montre parfois de l’instabilité. Cette instabilité se produit généralement quand la taille du pas ou le taux d’apprentissage, c’est-à-dire l’ajustement de chaque paramètre à chaque itération, est trop important. Les paramètres sont alors ajustés trop loin à chaque pas, et le modèle devient en fait pire avec chaque itération :

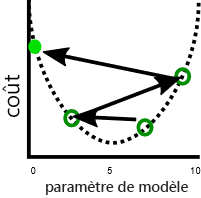
Tracé du coût par rapport au paramètre du modèle, qui montre le coût évoluant par grands pas, avec une diminution minimale du coût.

Un taux d’apprentissage plus lent peut résoudre ce problème, mais peut aussi introduire d’autres problèmes. Premièrement, des taux d’apprentissage plus lents peuvent signifier que l’entraînement dure longtemps, car davantage d’étapes sont nécessaires. Ensuite, des pas plus petits augmentent la probabilité que l’entraînement se stabilise sur un minimum local :

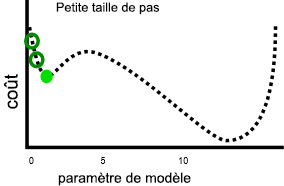
Tracé du coût par rapport au paramètre du modèle, montrant de petits mouvements dans le coût.

En revanche, un taux d’apprentissage plus rapide peut permettre d’éviter plus facilement d’atteindre des minima locaux, car des pas plus grands peuvent éviter les maxima locaux :

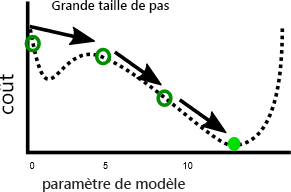
Tracé du coût par rapport au paramètre du modèle, avec des mouvements réguliers dans le coût jusqu’à ce qu’un minimum soit atteint.

Comme le montre l’exercice suivant, à chaque problème correspond une taille de pas optimale. Trouver cette valeur optimale est quelque chose qui nécessite souvent une expérimentation.