Arbres de décision et architecture de modèle
Lorsque nous parlons d’architecture, nous pensons souvent aux bâtiments. L’architecture est la base de la structure d’une construction : sa hauteur, sa profondeur, le nombre d’étages et la façon dont les éléments sont reliés en interne. Cette architecture dicte également la manière dont nous utilisons un bâtiment : par où nous pouvons y entrer et ce que nous pouvons « en tirer », en pratique.
Dans le monde du Machine Learning, l’architecture renvoie à un concept similaire. Combien de paramètres possède-t-il et comment sont-ils liés pour parvenir à un calcul ? Calculons-nous un grand nombre en parallèle (largeur) ou avons-nous des opérations en série qui reposent sur un calcul précédent (profondeur) ? Comment pouvons-nous fournir des entrées à ce modèle et comment pouvons-nous recevoir des sorties ? Ces décisions architecturales s’appliquent généralement seulement à des modèles plus complexes, et les décisions architecturales peuvent aller du simple au complexe. Ces décisions sont généralement prises avant l’apprentissage du modèle, mais dans certaines circonstances, il est possible d’apporter des modifications après l’apprentissage.
Nous allons étudier cela plus concrètement avec les arbres de décision.
Qu’est-ce qu’un arbre de décision ?
En résumé, un arbre de décision est un ordinogramme. Les arbres de décision sont un modèle de catégorisation qui décompose les décisions en plusieurs étapes.
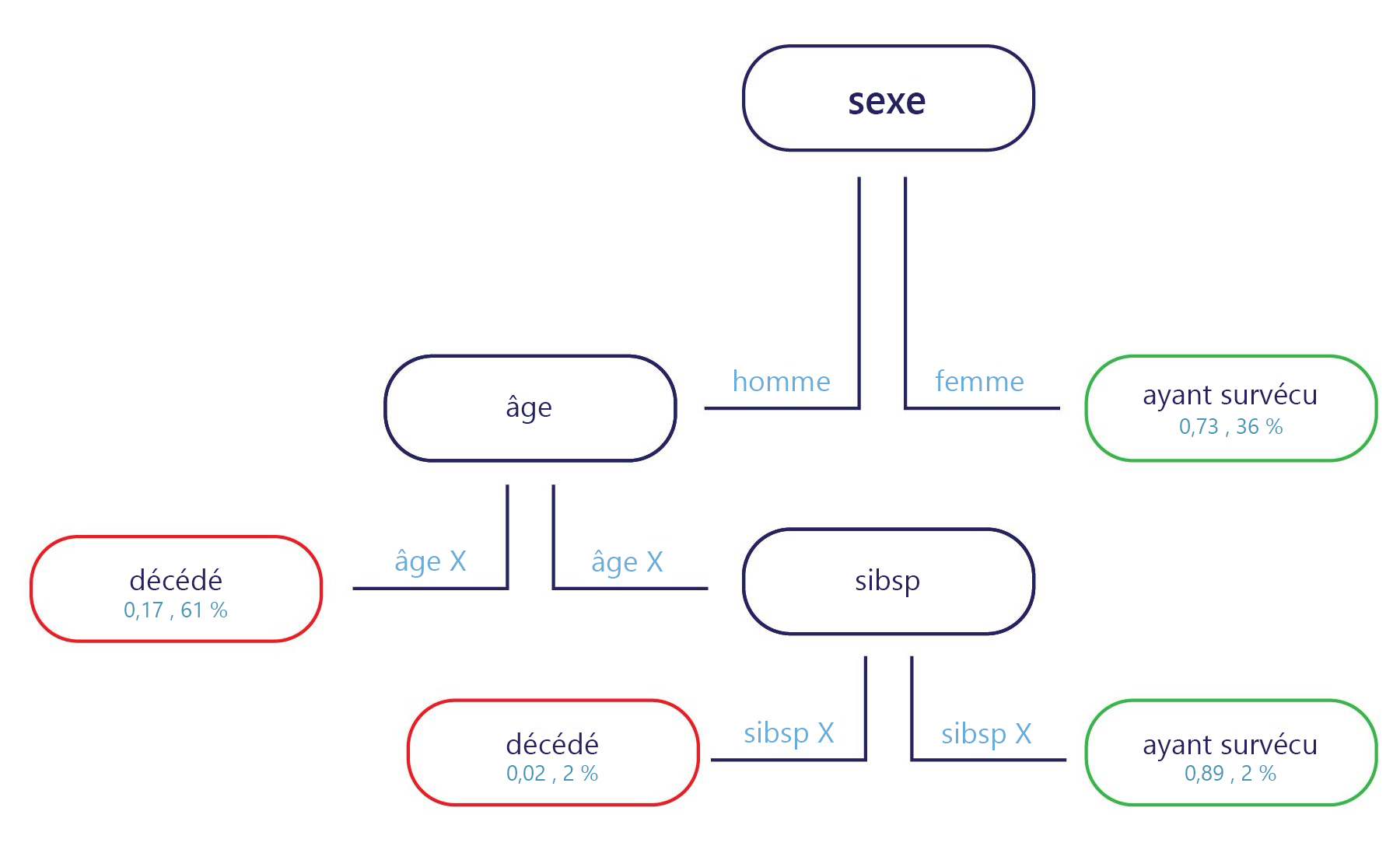
L’échantillon, s’il est fourni au point d’entrée (en haut, dans le diagramme ci-dessus) et à chaque point de sortie, est étiqueté (en bas du diagramme). Au niveau de chaque nœud, une instruction « if » simple détermine la branche à laquelle passe l’échantillon. Une fois que la branche a atteint la fin de l’arbre (les feuilles), elle est étiquetée.
Comment les arbres de décision sont-ils entraînés ?
Les arbres de décision sont entraînés selon un nœud ou un point de décision à la fois. Sur le premier nœud, l’ensemble d’apprentissage est évalué. À partir de là, une fonctionnalité est sélectionnée ; elle peut mieux séparer l’ensemble en deux sous-ensembles qui ont des étiquettes plus homogènes. Par exemple, imaginez que notre ensemble d’apprentissage est le suivant :
| Poids (fonctionnalité) | Âge (fonctionnalité) | Vainqueur d’une médaille (étiquette) |
|---|---|---|
| 90 | 18 | Non |
| 80 | 20 | Non |
| 70 | 19 | Non |
| 70 | 25 | Non |
| 60 | 18 | Oui |
| 80 | 28 | Oui |
| 85 % | 26 | Oui |
| 90 | 25 | Oui |
Si nous faisons de notre mieux pour trouver une règle afin de fractionner ces données, nous pouvons les fractionner par âge, à environ 24 ans, car la plupart des vainqueurs de médailles ont plus de 24 ans. Ce fractionnement nous donnera deux sous-ensembles de données.
Sous-ensemble 1
| Poids (fonctionnalité) | Âge (fonctionnalité) | Vainqueur d’une médaille (étiquette) |
|---|---|---|
| 90 | 18 | Non |
| 80 | 20 | Non |
| 70 | 19 | Non |
| 60 | 18 | Oui |
Sous-ensemble 2
| Poids (fonctionnalité) | Âge (fonctionnalité) | Vainqueur d’une médaille (étiquette) |
|---|---|---|
| 70 | 25 | Non |
| 80 | 28 | Oui |
| 85 % | 26 | Oui |
| 90 | 25 | Oui |
Si nous nous arrêtons ici, nous avons un modèle simple avec un nœud et deux feuilles. La feuille 1 contient des vainqueurs non médaillés et est précise à 75 % dans notre ensemble d’apprentissage. La feuille 2 contient des vainqueurs médaillés et est également précise à 75 % dans notre ensemble d’apprentissage.
Cependant, nous n’avons pas besoin de nous arrêter ici. Nous pouvons poursuivre ce processus en fractionnant encore les feuilles.
Dans le sous-ensemble 1, le premier nouveau nœud peut être fractionné par poids, car le seul vainqueur médaillé est plus léger que les personnes qui n’ont pas remporté de médaille. La règle peut être définie sur « poids < 65 ». Cela prédit que les personnes associées à la règle poids < 65 auraient remporté une médaille, tandis que toute personne associée à la règle poids ≥ 65 ne respecte pas ce critère et la prévision pourrait donc être qu’elles n’auraient pas remporté de médaille.
Dans le sous-ensemble 2, le second nœud peut également être fractionné par poids, mais cette fois prédit que toute personne dont le poids est supérieur à 70 kg aurait gagné une médaille, tandis que les autres non.
Nous obtenons alors un arbre dont la précision pourrait atteindre 100 % sur l’ensemble d’apprentissage.
Forces et faiblesses des arbres de décision
Les arbres de décision ont en général un biais faible. Cela signifie qu’ils sont généralement utiles pour identifier les fonctionnalités importantes afin d’étiqueter correctement un élément.
La principale faiblesse des arbres de décision est le surajustement. Prenons l’exemple précédent : le modèle offre une méthode exacte pour calculer qui est susceptible de remporter une médaille, et cela prédit correctement 100 % de l’ensemble de données d’entraînement. Ce niveau de précision est inhabituel pour les modèles Machine Learning, qui commettent normalement de nombreuses erreurs sur les ensembles de données d’apprentissage. Des performances d’apprentissage satisfaisantes ne constituent pas un inconvénient en soi, mais l’arbre est devenu si spécialisé dans l’ensemble d’apprentissage qu’il n’est sans doute pas performant sur l’ensemble de tests. Pourquoi ? Parce que l’arbre est parvenu à apprendre les relations dans l’ensemble d’entraînement qui ne sont probablement pas réelles, par exemple un poids de 60 kg garantit une médaille si vous avez moins de 25 ans.
L’architecture du modèle influe sur le surajustement
La structure de notre arbre de décision est essentielle pour éviter ses faiblesses. Plus l’arbre est profond, plus il est probable qu’il surajuste l’ensemble d’entraînement. Par exemple, dans l’arbre simple ci-dessus, si nous limitions l’arbre au premier nœud, cela entraînerait des erreurs sur l’ensemble d’apprentissage, mais la précision serait probablement meilleure sur l’ensemble de tests. Pourquoi ? Parce que l’arbre aurait des règles plus générales sur les vainqueurs de médaille, par exemple « les athlètes de plus de 24 ans », plutôt que des règles extrêmement spécifiques qui ne peuvent s’appliquer qu’à l’ensemble d’entraînement.
Bien que nous nous concentrions ici sur les arbres, d’autres modèles complexes présentent souvent des faiblesses similaires que nous pouvons atténuer par le biais de décisions sur la façon dont elles sont structurées, ou sur la façon dont elles sont autorisées à être manipulées par l’entraînement.