Régression polynomiale
Jusqu’à maintenant, nous avons uniquement examiné les modèles de régression linéaire, en d’autres termes les modèles qui peuvent être modélisés sous forme de lignes droites. Les modèles de régression peuvent, quant à eux, fonctionner avec pratiquement tous les autres types de relations.
Qu'est-ce que la régression polynomiale ?
La régression polynomiale modélise les relations sous la forme d'un type particulier de courbe. Les polynômes sont une famille de courbes, allant des formes simples aux formes complexes. Plus il y a de paramètres dans l'équation (modèle), plus la courbe peut être complexe.
Par exemple, un polynôme à deux paramètres est une ligne droite :
y = point d'intersection + B1*x
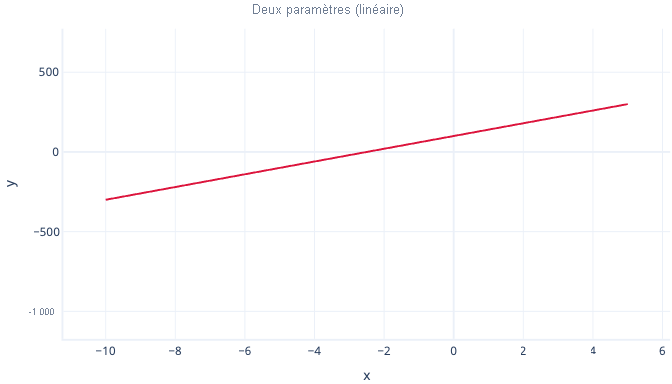
Alors qu'un polynôme à trois paramètres comporte une courbure :
y = point d'intersection + B1*x + B2 * x2
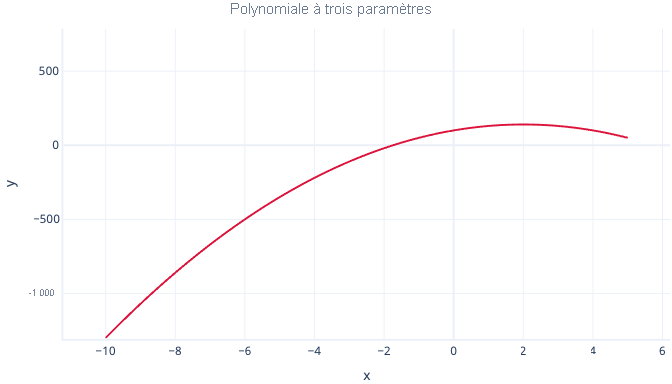
Et un polynôme à quatre paramètres peut comporter deux courbures :
y = point d'intersection + B1*x + B2 * x2 + B3 * x3
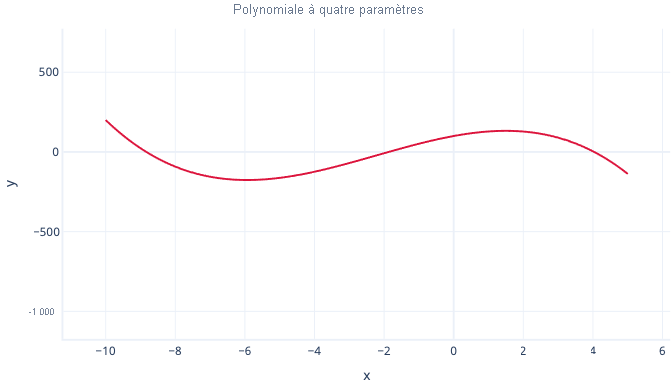
Courbes polynomiales et autres courbes
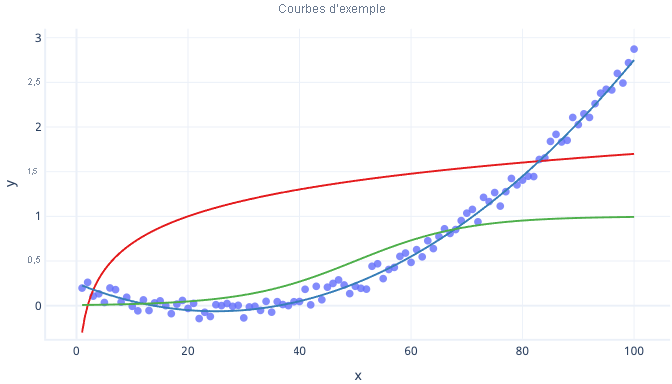
Il existe de nombreux genres de courbe, par exemple les courbes logarithmiques et les courbes logistiques (en forme de S), qui peuvent toutes être utilisées avec la régression.
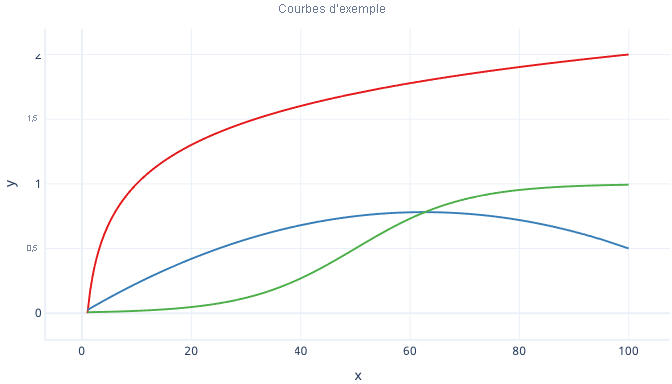
L’un des principaux avantages de la régression polynomiale est que vous pouvez l’utiliser pour examiner toutes sortes de relations. Par exemple, vous pouvez utiliser la régression polynomiale pour les relations négatives dans une certaine plage de valeurs de caractéristiques, mais positives dans d’autres. Vous pouvez également l’utiliser quand l’étiquette (valeur y) n’a aucune limite supérieure théorique.
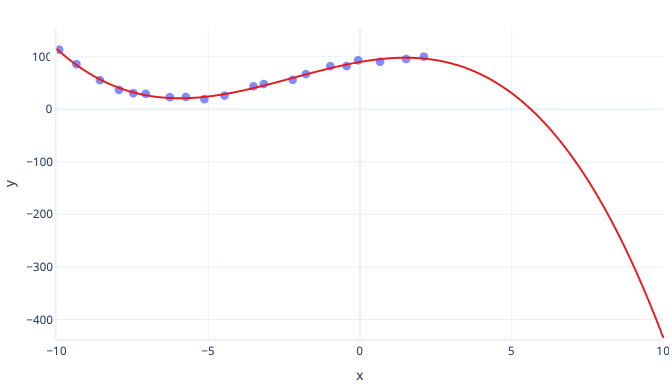
L'inconvénient majeur des courbes polynomiales est que leur extrapolation est souvent médiocre. En d'autres termes, si nous essayons de prédire des valeurs plus grandes ou plus petites que nos données d'apprentissage, les polynômes peuvent prédire des valeurs extrêmes irréalistes. Autre inconvénient, les courbes polynomiales peuvent facilement être surajustées. Cela signifie que le bruit associé aux données peut modifier la forme de la courbe, beaucoup plus que les modèles plus simples comme la régression linéaire simple.
Les courbes peuvent-elles être utilisées avec plusieurs caractéristiques ?
Nous avons vu comment la régression multiple permet d'ajuster plusieurs relations linéaires en même temps. Mais ces relations ne doivent pas nécessairement se limiter aux relations linéaires. Des courbes de toutes sortes peuvent être utilisées, le cas échéant. Toutefois, vous devez veiller à ne pas utiliser de courbes telles que des polynômes avec plusieurs caractéristiques quand elles ne sont pas nécessaires. En effet, les relations peuvent s’avérer très complexes, ce qui rend plus difficile la compréhension des modèles et l’évaluation du réalisme de leurs prédictions.