Vecteurs, sommets et quaternions

Dans Direct3D, les sommets décrivent la position et l’orientation. Chaque sommet d’une primitive est décrit par un vecteur qui donne sa position, sa couleur, ses coordonnées de texture et un vecteur normal qui donne son orientation.

Les quaternions ajoutent un quatrième élément aux valeurs [x, y, z] qui définissent un vecteur à trois composants. Les quaternions sont une alternative aux méthodes de matrice qui sont généralement utilisées pour les rotations 3D. Un quaternion représente un axe dans l’espace 3D et une rotation autour de cet axe. Par exemple, un quaternion peut représenter un axe (1,1,2) et une rotation de 1 radian. Les Quaternions contiennent des informations précieuses, mais leur véritable pouvoir provient des deux opérations que vous pouvez effectuer sur eux : la composition et l’interpolation.

L’exécution de la composition sur les quaternions est similaire à leur combinaison. La composition de deux quaternions n’est pas notée comme l’illustration suivante.

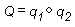
La composition de deux quaternions appliqués à une géométrie signifie « faire pivoter la géométrie autour de l’axe par rotation », puis la faire pivoter autour de l’axe₁ par rotation₁ ». Dans ce cas, Q représente une rotation autour d’un seul axe qui est le résultat de l’application de q...), puis q₁ à la géométrie.

À l’aide de l’interpolation de quaternion, une application peut calculer un chemin lisse et raisonnable d’un axe et d’une orientation vers un autre. Par conséquent, l’interpolation entre q₁ et q₁ fournit un moyen simple d’animer d’une orientation à une autre.

Lorsque vous utilisez ensemble la composition et l’interpolation, ils vous fournissent un moyen simple de manipuler une géométrie d’une manière qui semble complexe. Par exemple, imaginez que vous disposez d’une géométrie que vous souhaitez faire pivoter vers une orientation donnée. Vous savez que vous souhaitez la faire pivoter en degrés r₁ autour de l’axe, mais vous ne connaissez pas le quaternion final. En utilisant la composition, vous pouvez combiner les deux rotations sur la géométrie pour obtenir un quaternion unique qui est le résultat. Ensuite, vous pouvez interpoler de l’original au quaternion composé pour obtenir une transition fluide de l’un à l’autre.

Rubriques connexes

Systèmes de coordonnées et géométrie