Fonction D3DXSHEvalHemisphereLight (D3dx9math.h)
Notes
La bibliothèque d’utilitaires D3DX (D3DX 9, D3DX 10 et D3DX 11) est déconseillée et n’est pas prise en charge pour les applications du Windows Store.
Notes
Au lieu d’utiliser cette fonction, nous vous recommandons d’utiliser la fonction de bibliothèque Spherical Harmonics MathXMSHEvalHemisphereLight.
Évalue une lumière qui est une interpolation linéaire entre deux couleurs sur la sphère.
Syntaxe
HRESULT D3DXSHEvalHemisphereLight(
_In_ UINT Order,
_In_ const D3DXVECTOR3 *pDir,
_In_ D3DXCOLOR Top,
_In_ D3DXCOLOR Bottom,
_In_ FLOAT *pROut,
_In_ FLOAT *pGOut,
_In_ FLOAT *pBOut
);
Paramètres
-
Ordre [in]
-
Type : UINT
Ordre de l’évaluation harmonique sphérique (SH). Doit être dans la plage de D3DXSH_MINORDER à D3DXSH_MAXORDER, inclusive. L’évaluation génère des coefficients Order². Le degré de l’évaluation est Order - 1.
-
pDir [in]
-
Type : const D3DXVECTOR3*
Pointeur vers le vecteur de direction de l’axe de l’hémisphère (x, y, z) dans lequel évaluer les fonctions de base SH. Consultez la section Notes.
-
Haut [in]
-
Type : D3DXCOLOR
Couleur du ciel.
-
Bas [in]
-
Type : D3DXCOLOR
Couleur du sol.
-
pROut [in]
-
Type : FLOAT*
Pointeur vers le vecteur SH de sortie pour le composant rouge.
-
pGOut [in]
-
Type : FLOAT*
Pointeur vers le vecteur SH de sortie pour le composant vert.
-
pBOut [in]
-
Type : FLOAT*
Pointeur vers le vecteur SH de sortie pour le composant bleu.
Valeur retournée
Type : HRESULT
Si la fonction réussit, la valeur de retour est D3D_OK. Si la fonction échoue, la valeur de retour peut être : D3DERR_INVALIDCALL.
Notes
L’interpolation est effectuée linéairement entre les deux points, et non sur la surface de la sphère (autrement dit, si l’axe était (0,0,1), il est linéaire en Z, et non dans l’angle azimutal). La fonction d’éclairage sphérique résultante est normalisée de sorte qu’un point sur une surface parfaitement diffuse sans ombrage et un pointage normal dans la direction pDir entraînerait un éclat de sortie avec la valeur 1 (si la couleur du haut était blanche et la couleur du bas était noire). Il s’agit d’un modèle très simple où Top représente l’intensité du « ciel » et Bottom représente l’intensité du « sol ».
Sur la sphère avec rayon d’unité, comme le montre l’illustration suivante, la direction peut être spécifiée simplement avec téta, l’angle autour de l’axe z dans le sens droitier, et phi, l’angle à partir de z.
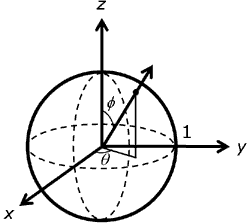
Les équations suivantes montrent la relation entre les coordonnées cartésiennes (x, y, z) et sphériques (the, phi) sur la sphère d’unité. L’angle 0 à 2 pi varie sur la plage de 0 à 2 pi, tandis que phi varie de 0 à pi.
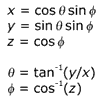
Spécifications
| Condition requise | Valeur |
|---|---|
| En-tête |
|
| Bibliothèque |
|
Voir aussi