Types de lumière (Direct3D 9)
La propriété type de lumière définit le type de source de lumière que vous utilisez. Le type de lumière est défini à l’aide d’une valeur de l’énumération D3DLIGHTTYPE C++ dans le membre Type de la structure D3DLIGHT9 de la lumière. Il existe trois types de lumières dans Direct3D : les lumières pointées, les projecteurs et les lumières directionnelles. Chaque type éclaire les objets d’une scène différemment, avec différents niveaux de surcharge de calcul.
Lumière de point
Les lumières ponctuelles ont une couleur et une position dans une scène, mais pas de direction unique. Ils dégagent la lumière de façon égale dans toutes les directions, comme le montre l’illustration suivante.
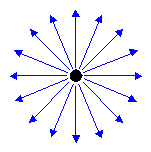
Une ampoule est un bon exemple de lumière ponctuelle. Les lumières ponctuelles sont affectées par l’atténuation et la portée, et illuminent un maillage sur une base vertex par sommet. Pendant l’éclairage, Direct3D utilise la position de la lumière ponctuelle dans l’espace mondial et les coordonnées du vertex allumé pour dériver un vecteur pour la direction de la lumière et la distance parcourue par la lumière. Les deux sont utilisés, ainsi que la normale du vertex, pour calculer la contribution de la lumière à l’éclairage de la surface.
Lumière directionnelle
Les lumières directionnelles ont uniquement la couleur et la direction, pas la position. Ils émettent de la lumière parallèle. Cela signifie que toute la lumière générée par les lumières directionnelles traverse une scène dans la même direction. Imaginez une lumière directionnelle comme une source de lumière à une distance quasi infinie, comme le soleil. Les lumières directionnelles ne sont pas affectées par l’atténuation ou la plage, de sorte que la direction et la couleur que vous spécifiez sont les seuls facteurs pris en compte lorsque Direct3D calcule les couleurs de vertex. En raison du petit nombre de facteurs d’éclairage, il s’agit des lumières les moins gourmandes en ressources de calcul à utiliser.
Projecteur
Les projecteurs ont la couleur, la position et la direction dans laquelle ils émettent de la lumière. La lumière émise par un projecteur est constituée d’un cône interne brillant et d’un cône externe plus grand, l’intensité lumineuse diminuant entre les deux, comme le montre l’illustration suivante.

Les projecteurs sont affectés par les retombées, l’atténuation et la portée. Ces facteurs, ainsi que la distance parcourue par la lumière jusqu’à chaque sommet, sont compris dans lors du calcul des effets d’éclairage pour les objets d’une scène. Le calcul de ces effets pour chaque sommet rend les projecteurs les plus gourmands en calcul de toutes les lumières dans Direct3D.
La structure C++ D3DLIGHT9 contient trois membres qui sont utilisés uniquement par les projecteurs. Ces membres - Falloff, Theta et Phi - contrôlent la taille ou la taille des cônes intérieurs et externes d’un objet vedette, et la façon dont la lumière diminue entre eux.
La valeur Téta est l’angle radian du cône interne du projecteur, et la valeur Phi est l’angle du cône externe de lumière. La valeur Falloff contrôle la façon dont l’intensité lumineuse diminue entre le bord externe du cône interne et le bord interne du cône externe. La plupart des applications définissent Falloff sur 1.0 pour créer un repli qui se produit uniformément entre les deux cônes, mais vous pouvez définir d’autres valeurs si nécessaire.
L’illustration suivante montre la relation entre les valeurs de ces membres et comment elles peuvent affecter les cônes de lumière intérieurs et externes d’un projecteur.
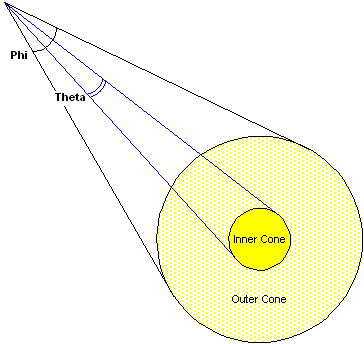
Les projecteurs émettent un cône de lumière qui a deux parties : un cône intérieur lumineux et un cône externe. La lumière est la plus brillante dans le cône intérieur et n’est pas présente à l’extérieur du cône externe, avec une intensité lumineuse atténuée entre les deux zones. Ce type d’atténuation est communément appelé « falloff ».
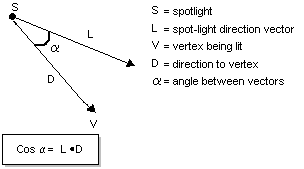
La quantité de lumière qu’un sommet reçoit est basée sur l’emplacement du vertex dans les cônes internes ou externes. Direct3D calcule le produit en point du vecteur de direction (L) de la lumière et du vertex (D). Cette valeur est égale au cosinus de l’angle entre les deux vecteurs et sert d’indicateur de la position du vertex qui peut être comparée aux angles de cône de la lumière pour déterminer où le sommet peut se trouver dans les cônes internes ou externes. L’illustration suivante fournit une représentation graphique de l’association entre ces deux vecteurs.
Le système compare cette valeur au cosinus des angles de cône intérieur et externe du projecteur. Dans la structure D3DLIGHT9 de la lumière, les membres Theta et Phi représentent les angles coniques totaux pour les cônes internes et externes. Étant donné que l’atténuation se produit lorsque le sommet devient plus éloigné du centre de l’éclairage (plutôt que sur l’angle cône total), le runtime divise ces angles de cône en deux avant de calculer leurs cosinus.
Si le produit de point des vecteurs L et D est inférieur ou égal au cosinus de l’angle cône externe, le sommet se trouve au-delà du cône externe et ne reçoit aucune lumière. Si le produit de point de L et D est supérieur au cosinus de l’angle du cône interne, le sommet se trouve dans le cône interne et reçoit la quantité maximale de lumière, toujours en tenant compte de l’atténuation sur la distance. Si le vertex se trouve quelque part entre les deux régions, l’issue est calculée à l’aide de l’équation suivante.
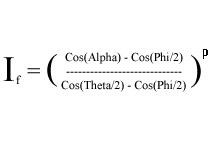
Où :
- I f est l’intensité de la lumière après la chute
- Alpha est l’angle entre les vecteurs L et D
- Theta est l’angle de cône interne
- Phi est l’angle cône externe
- p est la chute
Cette formule génère une valeur comprise entre 0,0 et 1,0 qui met à l’échelle l’intensité de la lumière au sommet pour tenir compte des retombées. L’atténuation en tant que facteur de la distance du vertex par rapport à la lumière est également appliquée. Le graphique suivant montre comment différentes valeurs de repli peuvent affecter la courbe de repli.
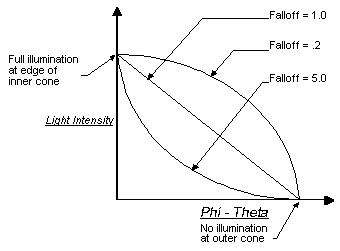
L’effet de diverses valeurs de repli sur l’éclairage réel est subtil, et une petite pénalité de performances est encourue en façonnant la courbe de repli avec des valeurs de repli autres que 1,0. Pour ces raisons, cette valeur est généralement définie sur 1.0.
Rubriques connexes