Parallel Computing – BigDays – Lamda-Expression-Trap I mentioned during the session – Understanding Bound and Free Variables in Lamdas
At my session on parallel computing at BigDays 2010 during my first demo I mentioned a potential trap with lamda-expressions and ThreadPool.QueueUserWorkItem(). Thanks to Philipp Aumayr from timecockpit.com – based on a question he asked when he watched the demo in Graz, in the break afterwards together we uncovered a very dangerous trap when it comes to lamda-expressions and ThreadPool.QueueUserWorkItem!
So, what is the trap all about and what’s the problem? In the BigDays-Vienna-delivery I added this hint to my presentation and here I am going to explain what happened.
The problem and its effects
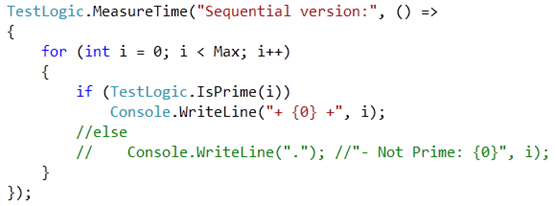
Suppose you have the following code you want to execute in parallel by using the ThreadPool and its QueueUserWorkItem()-method whereas every single cycle of the for-loop should be executed in parallel:
Of course the first obvious attempt of modifying this code to leverage the ThreadPool to execute calculations in parallel would result into the following one:
That was also my attempt when I prepared the demo for the very first time. But then something strange happened – the time-comparison between the sequential version (first code snippet) and the parallel version was more than strange.
It said, that for 50000 calculations, my parallel version required about 1050ms whereas my parallel version required just about 30ms. Man – what a performance optimization was that – a performance-improvement of a factor of 30 is not really realistic on a dual-core machine:)) … it’s basically impossible. So something must have been wrong with my code.
By taking a closer look at the results the console window in several test-runs I saw that it did actually not calculate most of the numbers and the results were totally incomplete. So what happened there? It skipped many of the prime numbers to calculate and to print as a result!?
The correct implementation and its explanation
Bound and Free variables in Lamda Expressions
An MSDN Magazine article explains the reason for this behavior very good – I’ll just explain it very short in this posting, if you want all the details, read this article. The wrong behavior of the implementation above is originated in the way Lambda-expressions are treated by the compiler and processed during runtime.
The primary thing you have to understand is the differentiation of bound and free variables.
- Bound variables are local variables or parameters explicitly passed to and defined as part of the lamda expression.
- Free variables are defined in the class or method that is containing the lamda expression. They are treated in a special way when it comes to the implementation of lamdas.
Free variables are captured into closure classes generated by the compiler at compile time and this closure holds these variables for the lamda as well as the address to the delegate for the lamda itself. Within one single scope in code, variables are always captured by the compiler and are re-written to the closure. Of course within the lamda, these free variables are accessed through the same closure all the time.
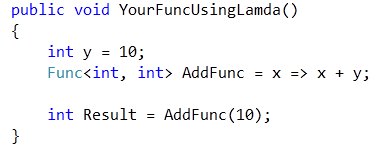
This is so important to understand, therefore lets start with a simple example. So, how does that affect your code? Suppose the following example (copied from the MSDN article mentioned earlier):
Conceptually and simplified demonstrated, the compiler creates a class containing the free variables and the implementation of the lamda. Then it creates a method for creating the lamda. The pseudo-code below shows, how that works conceptually – please note that this is simplified and does not match what the compiler is doing, exactly:
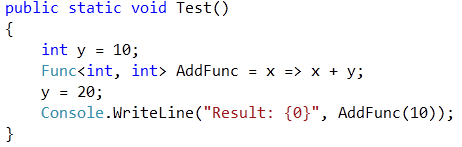
Now suppose you do the following thing: you declare and initialize a variable and assign a value to it. Then you declare the lamda, then you change the variable and finally you execute the lamda as follows:
At a first glance you would expect the value to be – 20 (y = 10, then AddFunc is declared and later executed). But in reality the value will be 30. Why is that? Well, very simple, because within this single scope within the method Test(), any assignments to y will be redirected to the Closure created by the compiler for the Lamda. Conceptually the compiler creates something like that:
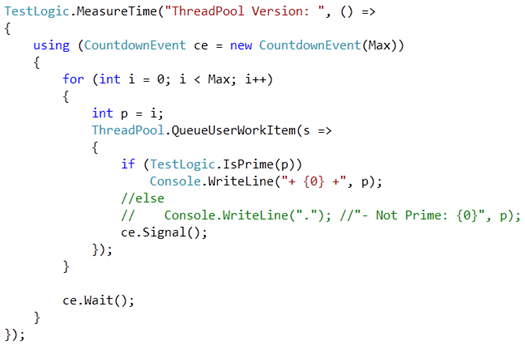
And that was exactly the problem that hit us with our ThreadPool-sample above and that I explained in my session at BigDays 2010. Just to remind you on the incorrect implementation, I repeat this code-snippet again:
In this implementation a closure is created that captures the lamda used for ThreadPool.QueueUserWorkItem() as well as the variable i in the context. Whenever the loop is moving on, the variable i is accessed through the closure.
Therefore our ThreadPool method gets the value of i that it has based on the loops situation at the time when the Thread starts. And therefore depending on when a thread starts and at which iteration the loop is a the time when the Thread starts, it will use the current value of i in the closure. As the thread created by ThreadPool.QueueUserWorkItem and the for-loop are accessing the same closure (which will be declared outside of the for-scope to capture both, the lamda and the for-loop), we are missing a lot of values in our execute.
To solve the problem we need to make sure that the closure is created within the scope of the for-loop. How can we do that? Well, simply create a new variable within the for-loop, assign the value i to this variable and use this variable as a free variable for our lamda expression. The following code snippet shows the correctly working code based on this knowledge:
The variable p above is created within the scope of one loop-iteration and we use it in the lamda. Therefore the code created by the compiler will create a closure within the for-loop’s scope using p – this closure of course will be created separately for each iteration of the loop. Therefore each Thread will get its own closure with the correct value assigned to it – and suddenly the behavior is correct, we get all our prime numbers and at are faster by parallel execution;)
I would strongly recommend reading the full article on MSDN magazine – just check out the following link to understand all the details:
https://msdn.microsoft.com/en-us/magazine/cc163362.aspx#S6
Feel free getting back to me if you have any questions!