Basi delle Reti Neurali in Visual Basic .NET (it-IT)
Info
Emiliano published a copy on his GitHub but no longer for VB.NET. Here's the C# version, proposed as a library: https://github.com/EmilianoMusso/emNeuralNetwork
Finalità
In questo articolo (spero il primo di una piccola serie), vedremo come implementare una rete neurale in Visual Basic .NET, ovvero un modello capace di processare dei dati in input, aggiustando la sua meccanica interna per imparare a produrre un risultato desiderato. Vedremo più avanti cosa significhi questo. Il presente articolo si concentrerà sulle definizioni generali relative alle reti neurali ed ai loro comportamenti, offrendo una loro semplice implementazione che il lettore sarà libero di testare. Nel paragrafo finale, scriveremo una rete neurale che sia capace di scambiare tra loro due variabili.
Introduzione
Una prima definizione
Il termine "rete neurale" è tipicamente usato in riferimento ad una rete, o circuito, costituita da neuroni. Possiamo differenziare due tipologie di reti neurali, ovvero: a) biologiche e b) artificiali. Naturalmente, parlando qui di sviluppo software, nel proseguo dell'articolo ci riferiremo alla seconda tipologia, ma questo genere di implementazioni attingono comunque il proprio modello base, nonché ispirazione, dalla loro controparte naturale; tenendo conto di ciò, può essere utile considerare il funzionamento di ciò che intendiamo quando parliamo di reti neurali biologiche.
Reti neurali naturali
Si tratta di reti costituite di neuroni biologici, tipiche delle creature viventi. I neuroni sono interconnessi tra loro nel sistema nervoso periferico o in quello centrale. Nelle neuroscienza, i gruppi di neuroni vengono identificati dalle funzioni fisiologiche che eseguono.
Reti neurali artificiali
Le reti artificiali sono i modelli matematici, implementabili attraverso sistemi elettronici ed informatici, che mimano il funzionamento di una rete biologica. Si tratta, in parole semplici, di avere un certo set di neuroni artificiali adatti a risolvere un particolare problema nel campo dell'intelligenza artificiale. Allo stesso modo di quelle naturali, una rete artificiale può "apprendere", attraverso il tempo e le prove, la natura di un problema, divenendo sempre più capace ed efficiente nella sua risoluzione.
Neuroni
Dopo questa breve premessa, diventa quindi ovvio che, in una rete, sia essa naturale o artificiale, l'entità conosciuta come "neurone" assume un'importanza capitale, in quanto ricevente degli input di rete e, in qualche modo, responsabile della corretta elaborazione dei dati, che produrranno un risultato. Pensiamo al nostro cervello: si tratta di un meraviglioso supercomputer dotato di circa 86*10^9 neuroni. Un numero strabiliante di entità che scambiano tra di loro informazioni in maniera costante, che corrono su 10^14 sinapsi. Come abbiamo detto, i modelli artificiali cercano di catturare e riprodurre il funzionamento di base di un neurone, che è basato su tre parti principali:
- Soma, o corpo cellulare
- Assone, la linea di uscita di un neurone
- Dendrita, linea di ingresso di un neurone, che riceve i dati da altri assoni attraverso le sinapsi
Il some esegue una somma pesata dei segnali in input, verificando l'eventuale eccedenza di un dato limite. Nel caso tale condizione si verifichi, il neurone viene attivato (risultando in un'azione potenziale), mentre permane in uno stato di quiete in caso contrario. Un modello artificiale cerca di replicare tali sottoparti, attraverso la creazione di un array di entità interconnesse capace di auto-tararsi sulla base degli input ricevuti, controllando costantemente i risultati prodotti rispetto ad un output atteso.
L'apprendimento di una rete neurale
Tipicamente, la teoria delle reti neurali identifica 3 metodi principali attraverso cui una rete apprende (dove, con "apprende" intenderemo da qui in avanti il processo attraverso cui la rete stessa si modifica per rendersi in grado di produrre un certo risultato a fronte di un input specifico). Riguardo all'implementazione in Visual Basic, ci riferiremo ad uno solo di questi metodi, ma è comunque utile introdurre la totalità dei paradigmi in gioco, in modo da avere una panoramica più completa. Affinchè una rete neurale possa apprendere, deve essere istruita (o allenata). L'allenamento di una rete può essere supervisionato, quando disponiamo di tuple di valori input/output. Attraverso di essi, una rete può imparare a costruire le relazioni che esistono tra i neuroni. Un altro metodo è il training non supervisionato, che si basa su algoritmi appositi, i quali modificheranno i pesi della rete in base ai dati in ingresso, risultando in reti che apprenderanno a raggruppare informazioni secondo metodi probabilistici. L'ultimo metodo è l'apprendimento rinforzato, che non si basa su dati da presentare alla rete, ma su algoritmi di esplorazione che produrranno input da sottoporre ad un agente, il quale verificherà l'impatto dei dati stessi sulla rete, tentando di identificare le performance di quest'ultima nella risoluzione di un dato problema. In questo articolo ci soffermeremo sul primo caso presentato, ovvero il training supervisionato.
Training supervisionato
Consideriamo questo metodo da una prospettiva più ravvicinata. Cosa significa addestrare una rete mediante supervisione? Come abbiamo visto, ciò riguarda prevalentemente il presentare alla rete dei set di dati in ingresso e attesi in uscita. Supponiamo di voler insegnare alla nostra rete come eseguire la somma di due numeri. In questo caso, seguendo il paradigma dell'addestramento supervisionato, dovremo sottoporre alla nostra rete dei dati di ingresso (diciamo [1;5]), ma anche renderle noto ciò che attendiamo come risultato (nel nostro caso, [6]). Quindi, un particolare algoritmo dovrà essere applicato per poter valutare lo stato corrente della rete, aggiustandola sulla base dei dati introdotti. Tale algoritmo, usato nel nostro esempio, è detto "di retropropagazione".
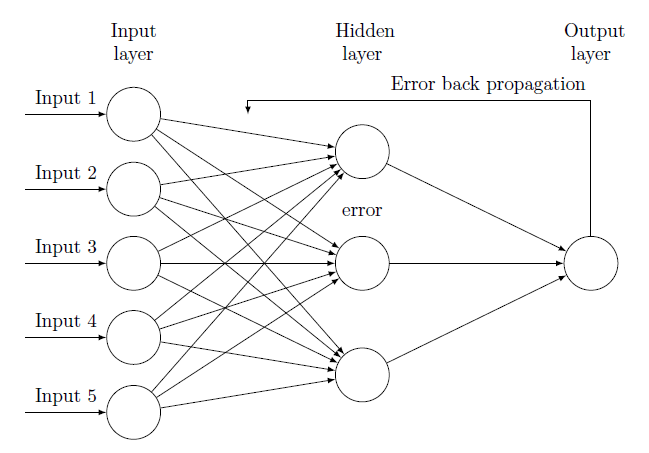
Retropropagazione
La retropropagazione degli errori è una tecnica secondo cui si inizializza la rete (tipicamente con valori casuali, che andremo ad assegnare ai pesi di ciascun neurone), procedendo poi nell'inoltrare i segnali in input e confrontando il risultato di rete con i valori attesi. A questo punto si calcola la deviazione tra l'effettivo prodotto e quello atteso, ottenendo un fattore delta che deve essere retropropagato ai nostri neuroni, per aggiustarne i valori iniziali in rispetto all'entità degli errori calcolati. Attraverso la ripetizione del processo, molti set di valori input/output verranno presentati alla rete, che ogni volta confronterà i dati reali con quelli ideali. In un dato tempo, questo tipo di operazione produrrà output sempre più precisi, calibrando il peso di ogni componente della rete, e raffinando di conseguenza la sua abilità di processare i dati ricevuti. Per un'estensiva spiegazione della retropropagazione, cfr. la sezione Bibliografia, al termine dell'articolo.
Creare una rete neurale
Dopo aver visto alcuni concetti preliminare sulle reti neurali, dovremo essere in grado di sviluppare un modello che risponda ai paradigmi illustrati. Senza eccedere in spiegazioni di tipo matematico, che non sono necessarie a meno di non volere approfondire ulteriormente il tema trattato, procederemo passo passo nella codifica di una rete semplice ma funzionale, che testeremo quando terminata. La prima cosa che dobbiamo considerare è la struttura di una rete neurale: sappiamo che è organizzata in neuroni, e che i neuroni sono interconnessi tra loro. Ma ignoriamo come.
Layer
Ed è a questo punto che fanno la loro comparsa i layers. Un layer è un gruppo di neuroni che condividono funzioni simili. Per esempio, pensiamo al punto di ingresso di una rete neurale, dove sono disposti i neuroni che riceveranno gli input. Quello sarà il layer di ingresso, lo strato che raggruppa tutti i neuroni dalla funzione simile, in questo caso limitata alla ricezione e trasmissione dei dati. Avremo sicuramente un layer di output, costituito dai neuroni che ricevono il risultato di elaborazioni pregresse. Tra questi layers, inoltre, ve ne possono risiedere un certo numero di altre tipologie, detti "nascosti" in quanto l'utente non deve potervi avere accesso diretto. Il numero di layer nascosti, così come il numero di neuroni che costituiscono ogni strato, dipende pesantemente dalla natura e complessità del problema che desideriamo risolvere. Per riassumere, ogni rete sarà costituita da strati, ciascuno dei quali conterrà un certo numero predeterminato di neuroni.
Neuroni e dendriti
Dal punto di vista artificiale, possiamo concepire un neurono come un'entità che espone un certo valore, il quale verrà aggiustato durante le iterazioni di addestramento, e legato ad altri neuroni attraverso i dendriti, che nel nostro caso saranno rappresentati da sotto-entità con un peso iniziale casuale. Il processo di training consisterà nel valorizzare i neuroni dello strato di input, i quali trasmetteranno il proprio valore agli strati superiori attraverso i dendriti. Negli strati più alti avverrà la stessa cosa, fino a che non sarà raggiunto lo strato di output. Infine, calcoleremo il delta tra l'output corrente e quello atteso, ripercorrendo la rete per aggiustare i pesi dei dendriti, il valore dei neuroni, e ciascun valore di deviazione, per correggere la rete stessa. Verrà quindi eseguito un nuovo round di addestramento.
Preparazione delle classi di rete
Avendo visto come una rete neurale sia strutturata, possiamo ora scrivere alcune classi attraverso cui gestiremo le varie entità di rete. Nello snippet che segue, delineerò le classi Dendrite, Neuron e Layer, che utilizzeremo congiuntamente nella stesura della classe NeuralNetwork
Classe Dendrite
Public Class Dendrite
Dim _weight As Double
Property Weight As Double
Get
Return _weight
End Get
Set(value As Double)
_weight = value
End Set
End Property
Public Sub New()
Me.Weight = r.NextDouble()
End Sub
End Class
Per prima cosa, la classe Dendrite: come si noterà, è costituita da una sola proprietà, denominata Weight. Nell'inizializzare un Dendrite, un valore casuale viene attribuito alla proprietà Weight. Il tipo della proprietà Weight è Double, in quanto i nostri valori di input saranno sempre un valore compreso tra zero ed uno, necessitando quindi di una precisione consistente quanto alle cifre decimali. Vedremo il perchè a breve. Non sono necessarie né previste altre proprietà o funzioni per questa classe.
Classe Neuron
Public Class Neuron
Dim _dendrites As New List(Of Dendrite)
Dim _dendriteCount As Integer
Dim _bias As Double
Dim _value As Double
Dim _delta As Double
Public Property Dendrites As List(Of Dendrite)
Get
Return _dendrites
End Get
Set(value As List(Of Dendrite))
_dendrites = value
End Set
End Property
Public Property Bias As Double
Get
Return _bias
End Get
Set(value As Double)
_bias = value
End Set
End Property
Public Property Value As Double
Get
Return _value
End Get
Set(value As Double)
_value = value
End Set
End Property
Public Property Delta As Double
Get
Return _delta
End Get
Set(value As Double)
_delta = value
End Set
End Property
Public ReadOnly Property DendriteCount As Integer
Get
Return _dendrites.Count
End Get
End Property
Public Sub New()
Me.Bias = r.NextDouble()
End Sub
End Class
Successivamente, la classe Neuron. Come facilmente intuibile, esporrà una proprietà valore, Value, di tipo Double, per le stesse motivazioni viste sopra, ed una serie di potenziali Dendrite, il cui numero dipenderà dal numero di neuroni del layer a cui l'attuale neurone verrà connesso. Avremo quindi una proprietà Dendrite, una DendriteCount per la restituzione del numero di Dendrite, e due proprietà che ci serviranno durante il processo di ricalibrazione, ovvero Bias e Delta.
Classe Layer
Public Class Layer
Dim _neurons As New List(Of Neuron)
Dim _neuronCount As Integer
Public Property Neurons As List(Of Neuron)
Get
Return _neurons
End Get
Set(value As List(Of Neuron))
_neurons = value
End Set
End Property
Public ReadOnly Property NeuronCount As Integer
Get
Return _neurons.Count
End Get
End Property
Public Sub New(neuronNum As Integer)
_neuronCount = neuronNum
End Sub
End Class
In ultimo, la classe Layer, che è semplicemente un contenitore per un array di Neuron. Chiamandone il metodo New, l'utente dovrà indicare da quanti neuroni uno strato sia costituito. Vedremo nella prossima sezione come queste classi interagiscano nel contesto di una rete neurale completa.
Classe NeuralNetwork
La nostra classe NeuralNetwork può essere vista come una lista di strati (ciascuno dei quali eredità le proprietà delle classi sottostanti, ovvero neuroni e dendriti). Una rete neurale deve essere eseguita e addestrata, di conseguenza avremo sicuramente dei metodi utili a tale fine. L'inizializzazione della rete deve specificare, tra le altre cose, un parametro che chiameremo "tasso di apprendimento", ossia una variabile che andrà ad incidere nel ricalcolo dei pesi. Come il nome fa presupporre, il tasso di apprendimento (o learning rate) è un fattore che determina la velocità di apprendimento di una rete. Dal momento che si tratta di un fattore correttivo, il suo valore deve essere scelto accuratamente: se è troppo elevato, ma vi è una grossa presenza di possibilità di input, una rete potrebbe non apprendere correttamente. In generale, una buona abitudine è quella di impostare un tasso relativamente piccolo, per incrementarlo se la ricalibrazione della rete dovesse essere troppo lenta.
Vediamo un'implementazione della classe NeuralNetwork quasi completa:
Public Class NeuralNetwork
Dim _layers As New List(Of Layer)
Dim _learningRate As Double
Public Property Layers As List(Of Layer)
Get
Return _layers
End Get
Set(value As List(Of Layer))
_layers = value
End Set
End Property
Public Property LearningRate As Double
Get
Return _learningRate
End Get
Set(value As Double)
_learningRate = value
End Set
End Property
Public ReadOnly Property LayerCount As Integer
Get
Return _layers.Count
End Get
End Property
Sub New(LearningRate As Double, nLayers As List(Of Integer))
If nLayers.Count < 2 Then Exit Sub
Me.LearningRate = LearningRate
For ii As Integer = 0 To nLayers.Count - 1
Dim l As Layer = New Layer(nLayers(ii) - 1)
Me.Layers.Add(l)
For jj As Integer = 0 To nLayers(ii) - 1
l.Neurons.Add(New Neuron())
Next
For Each n As Neuron In l.Neurons
If ii = 0 Then n.Bias = 0
If ii > 0 Then
For k As Integer = 0 To nLayers(ii - 1) - 1
n.Dendrites.Add(New Dendrite)
Next
End If
Next
Next
End Sub
Function Execute(inputs As List(Of Double)) As List(Of Double)
If inputs.Count <> Me.Layers(0).NeuronCount Then
Return Nothing
End If
For ii As Integer = 0 To Me.LayerCount - 1
Dim curLayer As Layer = Me.Layers(ii)
For jj As Integer = 0 To curLayer.NeuronCount - 1
Dim curNeuron As Neuron = curLayer.Neurons(jj)
If ii = 0 Then
curNeuron.Value = inputs(jj)
Else
curNeuron.Value = 0
For k = 0 To Me.Layers(ii - 1).NeuronCount - 1
curNeuron.Value = curNeuron.Value + Me.Layers(ii - 1).Neurons(k).Value * curNeuron.Dendrites(k).Weight
Next k
curNeuron.Value = Sigmoid(curNeuron.Value + curNeuron.Bias)
End If
Next
Next
Dim outputs As New List(Of Double)
Dim la As Layer = Me.Layers(Me.LayerCount - 1)
For ii As Integer = 0 To la.NeuronCount - 1
outputs.Add(la.Neurons(ii).Value)
Next
Return outputs
End Function
Public Function Train(inputs As List(Of Double), outputs As List(Of Double)) As Boolean
If inputs.Count <> Me.Layers(0).NeuronCount Or outputs.Count <> Me.Layers(Me.LayerCount - 1).NeuronCount Then
Return False
End If
Execute(inputs)
For ii = 0 To Me.Layers(Me.LayerCount - 1).NeuronCount - 1
Dim curNeuron As Neuron = Me.Layers(Me.LayerCount - 1).Neurons(ii)
curNeuron.Delta = curNeuron.Value * (1 - curNeuron.Value) * (outputs(ii) - curNeuron.Value)
For jj = Me.LayerCount - 2 To 1 Step -1
For kk = 0 To Me.Layers(jj).NeuronCount - 1
Dim iNeuron As Neuron = Me.Layers(jj).Neurons(kk)
iNeuron.Delta = iNeuron.Value *
(1 - iNeuron.Value) * Me.Layers(jj + 1).Neurons(ii).Dendrites(kk).Weight *
Me.Layers(jj + 1).Neurons(ii).Delta
Next kk
Next jj
Next ii
For ii = Me.LayerCount - 1 To 0 Step -1
For jj = 0 To Me.Layers(ii).NeuronCount - 1
Dim iNeuron As Neuron = Me.Layers(ii).Neurons(jj)
iNeuron.Bias = iNeuron.Bias + (Me.LearningRate * iNeuron.Delta)
For kk = 0 To iNeuron.DendriteCount - 1
iNeuron.Dendrites(kk).Weight = iNeuron.Dendrites(kk).Weight + (Me.LearningRate * Me.Layers(ii - 1).Neurons(kk).Value * iNeuron.Delta)
Next kk
Next jj
Next ii
Return True
End Function
End Class
Metodo New()
Quando avremo inizializzato la nostra rete, essa richiederà un tasso di apprendimento, ed una lista di Layers. Processando tale lista, si nota come ciascun layer risulti nella generazione di neuroni e dendriti, assegnati ai rispettivi genitori. Chiamando il metodo New() dei neuroni e dei dendriti, avverrà un'assegnazione casuale dei loro valori iniziali e dei loro pesi. Se i layer passati sono meno di uno, la routine uscirà dal flusso, in quanto una rete neurale deve essere dotata di almeno due layer, input ed output.
Sub New(LearningRate As Double, nLayers As List(Of Integer))
If nLayers.Count < 2 Then Exit Sub
Me.LearningRate = LearningRate
For ii As Integer = 0 To nLayers.Count - 1
Dim l As Layer = New Layer(nLayers(ii) - 1)
Me.Layers.Add(l)
For jj As Integer = 0 To nLayers(ii) - 1
l.Neurons.Add(New Neuron())
Next
For Each n As Neuron In l.Neurons
If ii = 0 Then n.Bias = 0
If ii > 0 Then
For k As Integer = 0 To nLayers(ii - 1) - 1
n.Dendrites.Add(New Dendrite)
Next
End If
Next
Next
End Sub
Funzione Execute()
Come precedentemente detto, una rete deve possedere una funzione attraverso cui processare i dati di input, facendo in modo che essi vengono veicolati nella rete, raggiungendo lo strato di output. La funzione seguente realizza tale obiettivo. Per prima cosa, verificheremo la correttezza dei dati in ingresso: se il numero degli input differisce dal numero di neuroni del layer, la funzione non potrà essere eseguita. Ciascun neurone dovrà essere inizializzato. Per il primo layer, quello di input, assegneremo semplicemente la proprietà Value dei neuroni, in qualità di ingresso. Per gli altri layers, calcoleremo la somma pesata data dal valore attuale del neurone, più il valore del neurone del layer precedente, moltiplicato per il peso del dendrita. In ultimo, eseguiremo sul valore così calcolato la funzione sigmoide, che analizzeremo più sotto. Processando tutti i layers, il layer di uscita riceverà un risultato, che è il parametro che la nostra funzione restituirà al controllo del flusso di programma, sotto forma di List(Of Double).
Function Execute(inputs As List(Of Double)) As List(Of Double)
If inputs.Count <> Me.Layers(0).NeuronCount Then
Return Nothing
End If
For ii As Integer = 0 To Me.LayerCount - 1
Dim curLayer As Layer = Me.Layers(ii)
For jj As Integer = 0 To curLayer.NeuronCount - 1
Dim curNeuron As Neuron = curLayer.Neurons(jj)
If ii = 0 Then
curNeuron.Value = inputs(jj)
Else
curNeuron.Value = 0
For k = 0 To Me.Layers(ii - 1).NeuronCount - 1
curNeuron.Value = curNeuron.Value + Me.Layers(ii - 1).Neurons(k).Value * curNeuron.Dendrites(k).Weight
Next k
curNeuron.Value = Sigmoid(curNeuron.Value + curNeuron.Bias)
End If
Next
Next
Dim outputs As New List(Of Double)
Dim la As Layer = Me.Layers(Me.LayerCount - 1)
For ii As Integer = 0 To la.NeuronCount - 1
outputs.Add(la.Neurons(ii).Value)
Next
Return outputs
End Function
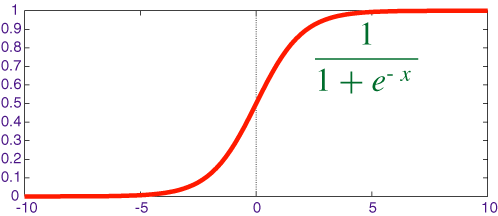
Funzione Sigmoid()
La sigmoide è una funzione matematica nota per la sua tipica forma ad "S". È definita per ciascun valore reale. Utilizziamo questa funzione nella programmazione di reti neurali a causa della sua differenziabilità - requisito della retropropagazione - ed inoltre perché introduce non-linearità nella rete stessa (rende cioè la rete in grado di apprendere la correlazione tra input che non producono combinazioni lineari). In più, per ciascun valore reale, la funzione sigmoide ritorna un valore tra zero ed uno (escluso il limite superiore). Questa funzione ha dunque caratteristiche che la rendono particolarmente adatta alla retropropagazione.
Funzione Train()
Una rete viene inizializzata con valori casuali, di conseguenza - senza ricalibrazione - i valori di ritorno saranno anch'essi piuttosto casuali. Senza una procedura di addestramento, una rete appena creata sarà quasi inutile. Definiamo, con il termine addestramento, il processo attraverso cui una rete neurale viene mantenuta attiva, continuando a fornirle input e confrontando i suoi risultati con quelli che si attendono. Trovando le differenze tra questi valori, procederemo nella ricalibrazione di ciascun peso e valore sulla rete, avvicinando sempre di più la rete alla produzione di quanto desideriamo.
In codice VB, qualcosa di questo tipo:
Public Function Train(inputs As List(Of Double), outputs As List(Of Double)) As Boolean
If inputs.Count <> Me.Layers(0).NeuronCount Or outputs.Count <> Me.Layers(Me.LayerCount - 1).NeuronCount Then
Return False
End If
Execute(inputs)
For ii = 0 To Me.Layers(Me.LayerCount - 1).NeuronCount - 1
Dim curNeuron As Neuron = Me.Layers(Me.LayerCount - 1).Neurons(ii)
curNeuron.Delta = curNeuron.Value * (1 - curNeuron.Value) * (outputs(ii) - curNeuron.Value)
For jj = Me.LayerCount - 2 To 1 Step -1
For kk = 0 To Me.Layers(jj).NeuronCount - 1
Dim iNeuron As Neuron = Me.Layers(jj).Neurons(kk)
iNeuron.Delta = iNeuron.Value *
(1 - iNeuron.Value) * Me.Layers(jj + 1).Neurons(ii).Dendrites(kk).Weight *
Me.Layers(jj + 1).Neurons(ii).Delta
Next kk
Next jj
Next ii
For ii = Me.LayerCount - 1 To 0 Step -1
For jj = 0 To Me.Layers(ii).NeuronCount - 1
Dim iNeuron As Neuron = Me.Layers(ii).Neurons(jj)
iNeuron.Bias = iNeuron.Bias + (Me.LearningRate * iNeuron.Delta)
For kk = 0 To iNeuron.DendriteCount - 1
iNeuron.Dendrites(kk).Weight = iNeuron.Dendrites(kk).Weight + (Me.LearningRate * Me.Layers(ii - 1).Neurons(kk).Value * iNeuron.Delta)
Next kk
Next jj
Next ii
Return True
End Function
Come sempre, verifichiamo la correttezza degli input, avviando poi la rete chiamando il metodo Execute(). Quindi, partendo dall'ultimo layer, processeremo ogni neurone e dendrita, correggendo ciascun valore applicando la differenza tra outputs. La stessa cosa faremo sui pesi dei dendriti, introducendo il tasso di apprendimento della rete, come visto sopra. Al termine di un round di addestramento (o, più realisticamente, al completamento di molte centinaia di round), inizieremo ad osservare che gli output prodotti dalla rete saranno sempre più precisi.
Una applicazione di test
In questa sezione vedremo una semplice applicazione di test, che utilizzeremo per creare una rete semplice, la cui finalità sarà l'esecuzione di un banale swap di variabili. Nel proseguo, considereremo una rete avente tre layers: uno strato di ingresso, costituito da due neuroni; un layer nascosto con quattro neuroni; uno strato di uscita con due neuroni. Ciò che ci aspettiamo dalla rete, una volta che sarà abbastanza addestrata, è la capacità di invertire i valori che le vengono presentati o, in altre parole, di trasferire il valore del neurone di input #1 sul neurone di output #2, e viceversa.
Nella versione scaricabile della classe NeuralNetwork troverete un paio di metodi qui non discussi, che si riferiscono al rendering grafico ed al debug testuale della rete. Li utilizzeremo in questo esempio, e potrete consultarli scaricando il sorgente allegato.
Inizializzare la rete
Utilizzando le nostre classi, una rete neurale potrà essere inizializzata semplicemente dichiarandola, e passandole un tasso di apprendimento e layers iniziali. Per esempio, nell'applicazione di test è visibile uno snippet del genere:
Dim network As NeuralNetwork
Private Sub Form1_Load(sender As Object, e As EventArgs) Handles MyBase.Load
Dim layerList As New List(Of Integer)
With layerList
.Add(2)
.Add(4)
.Add(2)
End With
network = New NeuralNetwork(21.5, layerList)
End Sub
Ho definito la mia rete globalmente rispetto al Form di avvio, poi - durante l'evento Load() - ho creato i layers di cui necessito, passandoli all'inizializzatore di rete. Ciò risulterà nel popolamento dei layer stessi mediante la creazione dei neuroni specificati, con ciascun elemento inizializzato in modo casuale quanto a valori, delta, bias, e pesi.
Eseguire una rete neurale
Avviare e addestrare una rete sono anch'esse procedure molto semplici. Tutto ciò che richiedono è l'esecuzione del metodo adatto, passando un set di valori di input/output. Nel caso del metodo Execute(), per lanciare la rete, potremmo ad esempio scrivere:
Dim inputs As New List(Of Double)
inputs.Add(txtIn01.Text)
inputs.Add(txtIn02.Text)
Dim ots As List(Of Double) = network.Execute(inputs)
txtOt01.Text = ots(0)
txtOt02.Text = ots(1)
Dove txtIn01, txtIn02, txtOt01, txtOt02 sono dei TextBoxes presenti sul Form. Ciò che abbiamo fatto con il codice di cui sopra è stato semplicemente di prendere il valore di due TextBoxes come input, scrivendo poi in un'altra coppia di TextBoxes i valori ritornati. La stessa procedura si applica in caso di addestramento.
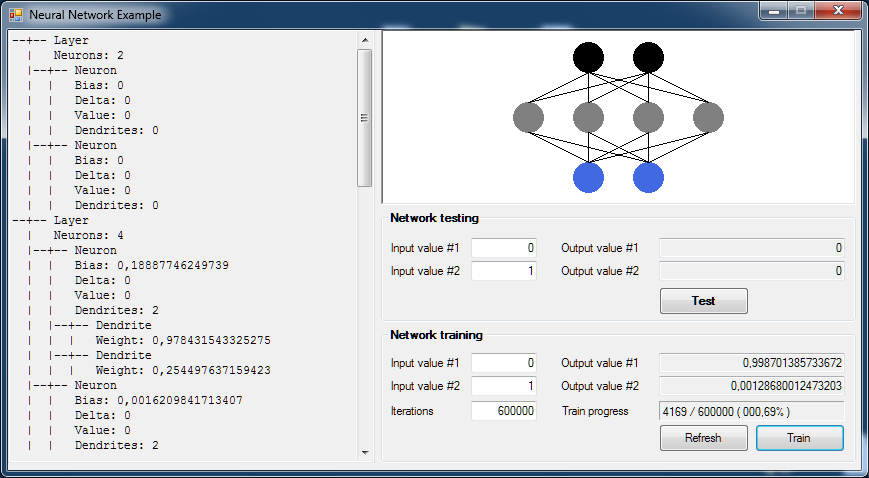
Scambiare due variabili
Nel video che segue, si può vedere una semplice sessione di addestramento. Il programma in esecuzione è lo stesso che è possibile scaricare al termine di questo articolo. Come si può notare, iniziando da valori casuali, la rete inizierà progressivamente ad apprendere come invertire i segnali che riceve. I valori di zero ed uno non vanno intesi come numeri precisi, bensì come "segnali di una certa intensità". Osservando i risultati dell'addestramento, si potrà notare come l'intensità dei valori crescerà verso uno, o decrescerà verso zero, senza mai toccare del tutto gli estremi, ma rappresentando una loro tendenza. Di conseguenza, al termine di una intensa sessione di addestramento, vedremo come, nel caso di una coppia in input del tipo [0;1], desiderando l'output [1;0], riceveremo un risultato simile a [0.999999998; 0.00000000015], dove i segnali di partenza sono rappresentazioni, per intensità, dei valori conducivi ad essi più vicini, comportandosi quindi come un vero neurone, la cui eccitabilità ed attivazione dipendono da soglie energetiche.
Codice sorgente
Il codice sorgente fin qui discusso può essere scaricato tramite il link: https://code.msdn.microsoft.com/Basis-of-Neural-Networks-a379549c
Bibliografia
Altre lingue
Il presente articolo è disponibile nelle seguenti localizzazioni: