[C#] Permutazioni nella risoluzione di uno Shikaku tramite bruteforcing (it-IT)
Introduzione
In questo articolo vedremo come sia possibile, tramite la stesura di un programma C#, risolvere uno Shikaku – gioco di logica giapponese – sfruttando la potenza computazionale delle nostre macchine per calcolare tutte le possibili combinazioni potenzialmente valide nella partita da svolgere, trovando poi tra esse l’unica valida. Sebbene l’approccio tramite bruteforcing (ovvero il calcolo progressivo di tutte le combinazioni possibili di un dato problema, fino al raggiungimento della soluzione valida) sia svantaggioso per elaborazioni con un numero elevato di possibilità, in questa sede esso verrà comunque impiegato per rendere più generico il problema, ed anche in quanto il focus dell’articolo non vuole essere quello della soluzione ottimale, quanto piuttosto l’analisi del processo che da un problema in parte “grafico” ci permette di dedurre un possibile approccio via codice.
Prima di passare alla parte pratica, vediamo pertanto nel dettaglio cosa sia lo Shikaku, per poi proporre un’idea di implementazione e quindi realizzarla.
Prerequisiti
- Microsoft Visual Studio
- Conoscenza di base del linguaggio C#
Shikaku, introduzione e regole
Shikaku (shikaku ni kire, dividere per quadrati) è un gioco di logica giapponese pubblicato da Nikoli Co. Ltd, editore specializzato in giochi, specialmente puzzle logici. Dello stesso editore, è – per fare un esempio – anche il più celebre Sudoku. Lo Shikaku (letteralmente, in lingua giapponese, quadrato) si gioca su una griglia di uguali righe e colonne, che può estendersi dalle dimensioni di 5 x 5 fino a 25 x 25 e oltre.
Alcune delle celle che costituiscono la griglia di gioco sono numerate. L’obiettivo del gioco è quello di dividere la griglia in rettangoli e quadrati tali per cui ciascuna di queste divisioni contenga uno solo dei numeri presenti, e che l’area di tale porzione sia pari al numero stesso. Ciò significa che due divisioni della griglia non possono sovrapporsi, ovvero condividere celle.
Riportiamo qui a seguire un esempio di Shikaku 11 x 11, con relativa soluzione:
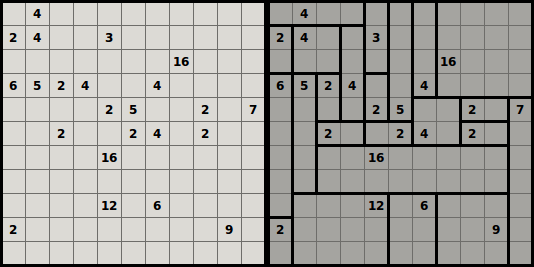
Griglie più piccole sono ovviamente più semplici da risolvere, e tuttavia si può essere tratti in inganno nel selezionare aree errate e dover ritornare sui propri passi, quando ci si rende conto – proseguendo nel gioco – che si è scelta una divisione che lascia scoperte celle, oppure che mette in condizione di non avere spazio necessario per soluzioni adiacenti. Nonostante questo, l’uomo è avvantaggiato dal poter vedere il problema, e quindi avere quantomeno un’idea delle proporzioni che ciascun rettangolo o quadrato dovranno avere. Non potendo replicare questa sensazione a livello macchina, dovremo necessariamente trovare un’altra strada per procedere.
Senz'altro, potremo partire dal concepire la griglia che compone l’intero Shikaku come un array bidimensionale (per esempio, di byte), con alcuni elementi dell’insieme che saranno inizializzati a valori conformi ad uno Shikaku valido. Ipotizzando di voler rappresentare una griglia 5 x 5, potremo cioè avere una struttura di questo tipo:
private const int _SIZE = 5;
public byte[,] Cells { get; set; } = new byte[_SIZE, _SIZE];
Proposta di soluzione del problema
Ciascuna cella contenente un valore può essere intesa come un problema a sé. Inizialmente, dovremo infatti preoccuparci di trovare tutte le soluzioni potenziali di ogni singola cella valorizzata, ovvero le aree che possono essere occupate per ogni valore, senza preoccuparci delle altre celle. In seconda battuta, confronteremo i risultati ottenuti per una cella con quelli di ciascuna altra cella, in modo da analizzare le collisioni tra aree. Si intuirà come quest’ultima parte sia senza dubbio computazionalmente impegnativa: tuttavia, mentre collezioniamo le varie soluzioni potenziali per ogni cella, non possiamo scartare alcuna di esse, poiché fintanto che non avremo tutte le possibili configurazioni per ogni cella valorizzata non saremo in grado di determinare il complesso delle collisioni. In altre parole, scartare una configurazione prima di ottenerle tutte e poterle confrontare si tradurrebbe nella possibile eliminazione di un elemento della sola soluzione valida.
Passiamo ad un esempio pratico che rappresenti quanto appena visto, e raffiguriamo qui a seguire il procedimento da adottare per trovare le possibili soluzioni a tre delle celle di uno shikaku 5 x 5. Nel caso in immagine, le celle [0,0], [4,0], [1,2]. Come si noterà, si procede ad elencare i possibili “movimenti” sulla griglia, ovvero – a partire dalla posizione della cella in esame – quali siano le direzioni in potersi allargare, fino ad ottenere l’area desiderata. In questa fase, come anticipato, non ci preoccuperemo delle soluzioni sovrapposte, ma va da sé che in seconda battuta, per esempio, la soluzione 2 della cella [4,0] sarà scartata, perché includerebbe la cella valorizzata [4,3].
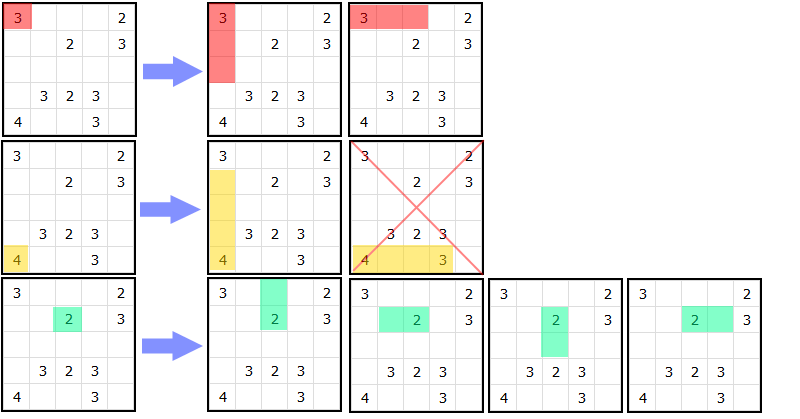
Si procede in questo modo per tutte le celle, e quando si è terminato il processo (ovvero, quando si dispone di tutte le soluzioni per ogni cella), si inizia a confrontarne le combinazioni, come se si sovrapponessero delle diapositive. Se le N diapositive sovrapposte (dove N è il numero delle celle valorizzate in origine) risultano non avere collisioni, si è trovata la soluzione corretta; viceversa, bisognerà proseguire nell’analisi delle restanti configurazioni.
Implementazione base
Passando all’implementazione pratica, cerchiamo quindi di concretizzare quanto visto fin qui: abbiamo parlato di un array bidimensionale per rappresentare la griglia, della necessità di calcolare l’estensione delle aree delle celle a valore, e la necessità di recuperare tutte le possibili soluzioni per una data cella. Vediamo un metodo per creare tutto questo facendo uso di C#.
public class Area
{
public int Base { get; set; }
public int Height { get; set; }
}
public class CellSolutions
{
public List<Shikaku> PotentialSolutions { get; set; }
}
public class Shikaku
{
private const int _SIZE = 5;
public byte[,] Cells { get; set; } = new byte[_SIZE, _SIZE];
public List<CellSolutions> Solutions { get; set; } = new List<CellSolutions>();
private List<Area> FindAreas(int area)
{
var tmp = new List<Area>();
for(var row = 0; row < _SIZE; row++)
{
for (var col = 0; col < _SIZE; col++)
{
if (row * col == area) tmp.Add(new Area() { Base = row, Height = col});
}
}
return tmp;
}
public Shikaku() { }
}
Quanto sopra è l’implementazione minima per ottenere il risultato premesso. Abbiamo tre classi, Area, CellSolutions, Shikaku. Quest’ultima sarà il cuore della nostra elaborazione. Come si noterà, possiede l’array bidimensionale di celle Cells, una List<CellSolutions> (che contiene una List<Shikaku>, e ci sarà utile ad immagazzinare le possibili soluzioni), ed infine la funzione FindAreas.
Si noti il suo funzionamento: essa necessita di un argomento che rappresenti il valore di un’area (ovvero, il numero rappresentato all’interno della nostra cella), e sulla base di questo – scorrendo le celle di griglia – va a calcolare tutte le possibili combinazioni di base per altezza che ottengono come risultato il valore stesso della cella. Viene quindi ritornata una List<Area>, che sarà utilizzata nel calcolo delle soluzioni possibili.
Quest’ultima può essere realizzata nel modo seguente:
private bool CompileArea(int row, int col, Area area, int rowToSolve, int colToSolve, int value)
{
var isCellInSolution = false;
int numOccupied = 0;
for(var r = row; r < row + area.Base; r++)
{
for(var c = col; c < col + area.Height; c++)
{
if (r < _SIZE && c < _SIZE)
{
++numOccupied;
this.Cells[r, c] = 99;
if (r == rowToSolve && c == colToSolve) isCellInSolution = true;
}
}
}
if (numOccupied != value) isCellInSolution = false;
return isCellInSolution;
}
Implementiamo cioè un metodo che riceva come parametro la posizione di riga/colonna (cella) da risolvere, un oggetto Area, ed il valore di area presente nella cella. Scorre quindi le righe e le colonne fino all'estensione massima di area.Base e area.Height, ed all’interno di tale ciclo verifica al tempo stesso di essere ancora all'interno della griglia. Quest’ultimo controllo è utile per evitare che aree che eccedono la griglia (ovvero, che abbiamo un numero di celle disponibili minori di quelle necessarie) siano considerate corrette.
Infine, si impone il valore di 99 alla cella considerata (supponendo di avere a che fare con Shikaku sufficientemente piccoli da non esporre mai 99 come valore iniziale di cella). Se tale cella ha le medesime coordinate di quella da risolvere, ritorniamo un booleano che indica che l’area coinvolge la nostra cella, dunque è candidata per essere una soluzione potenziale. Un ultimo controllo verifica che le celle selezionate combacino con il valore di cella: in caso negativo, l’area non deve essere considerata valida.
Utilizzeremo questo metodo nel contesto di un’ulteriore funzione, deputata a trovare tutte le possibili soluzioni di una singola cella
public List<Shikaku> SolveSingleCell(int row, int col)
{
var shikakus = new List<Shikaku>();
int value = this.Cells[row, col];
var areas = FindAreas(value);
for(var r = 0; r < _SIZE; r++)
{
for(var c = 0; c <_SIZE; c++)
{
foreach (var a in areas)
{
var shikaku = new Shikaku();
if (shikaku.CompileArea(r, c, a, row, col, value))
{
shikakus.Add(shikaku);
}
}
}
}
return shikakus;
}
Il metodo SolveSingleCell accetta come argomenti le coordinate di una cella da risolvere. Prepara quindi una lista di oggetti Shikaku, scorrendo per tutta la griglia le aree calcolate per il valore di cella, e verificando che ricadano nella cella selezionata, caso in cui considereremo lo shikaku calcolato come valido, ossia come potenziale soluzione eventualmente sovrapposta.
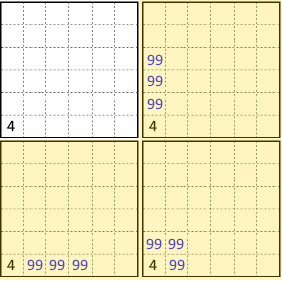
Ipotizzando quindi il caso di una cella da risolvere, vediamo quindi graficamente quale sarebbe il risultato del metodo SolveSingleCell, ovvero quali siano gli shikaku prodotti e restituiti (che, come si ricorderà, saranno considerabili al pari di “diapositive” da confrontare con quelle delle altre celle)
Possiamo allora pensare di immagazzinare queste tre possibili soluzioni nella List<CellSolutions> propria dello Shikaku di origine, in modo da potervi ritornare in seguito. Va da sé che per trovare tutte le possibili soluzioni di tutte le celle sia sufficiente iterare il metodo di cui sopra per ciascuna cella dello Shikaku originale, memorizzando i risultati restituiti per ogni cella.
public void GetAllSolutions()
{
for (var r = 0; r < _SIZE; r++)
{
for (var c = 0; c < _SIZE; c++)
{
if (this.Cells[r, c] > 0)
{
this.Solutions.Add(new CellSolutions() { PotentialSolutions = SolveSingleCell(r, c) });
}
}
}
}
Si nota nel metodo GetAllSolutions come, per ciascuna cella che abbia un valore superiore a zero, venga eseguito il metodo SolveSingleCell per compilare una lista potenziale di soluzioni. Al termine di questo ciclo avremo nella proprietà Solutions tanti oggetti quante saranno le celle dello Shikaku originale, e per ciascuna di esse la proprietà PotentialSolutions conterrà tutte le possibili soluzioni di cella. Non resterà quindi che confrontarle per trovare l’unica soluzione al problema iniziale.
Verifica delle permutazioni
Introduciamo un metodo banale ma importante: come possiamo infatti sapere se due Shikaku collidono tra loro? In altre parole, dobbiamo essere in grado di sapere se due possibili candidati cercano di occupare una o più celle comuni.
private bool IsColliding(Shikaku s1, Shikaku s2)
{
for(var r = 0; r <_SIZE; r++)
{
for(var c = 0; c < _SIZE; c++)
{
if (s1.Cells[r, c] == s2.Cells[r, c] && s1.Cells[r,c] == 99) return true;
}
}
return false;
}
Dati due oggetti Shikaku di uguali dimensioni, sarà sufficiente analizzare ogni loro cella, verificando che a parità di riga e colonna entrambe contengano il valore di 99. In quel caso, i due collidono. Se invece il test viene superato, i due quadrati sono potenzialmente compatibili perché non sovrapposti in alcun punto.
Grazie a tale metodo, possiamo ora pensare ad una funzione che controlli le permutazioni di ogni soluzione potenziale. Risolveremo tale problema pensandolo come un lucchetto con combinazione numerica. Infatti, si è poco sopra detto che la proprietà Solutions ha lunghezza pari a quella delle celle valorizzate, e che ogni Solutions[x] contiene tutte le possibili combinazioni che risolvono tale cella (PotentialSolutions).
Ipotizziamo di avere uno Shikaku con 5 celle valorizzate. Per ciascuna di esse, sono state calcolate rispettivamente 4, 2, 3, 6, 2 soluzioni potenziali. La proprietà Solutions, avente per ogni oggetto un numero variabile di PotentialSolutions potrà allora essere rappresentata come segue:
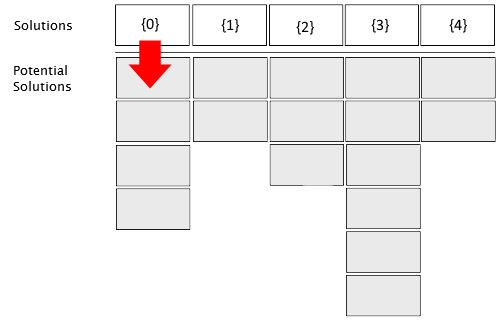
Conseguentemente a ciò, possiamo utilizzare un array unidimensionale (nel caso dell’esempio, di lunghezza 5), che scorreremo come fosse un lucchetto con combinazione, dove le possibilità di scorrere una certa posizione sono date dal numero di soluzioni potenziali per quella posizione. Ogni volta che in una Solutions si saranno esaurite le PotentialSolutions, si ritornerà a scorrerle a partire dall'indice zero. Per ciascuna configurazione testata, verranno verificate le collisioni tra ogni singolo Shikaku che compone la soluzione, e se queste si verificano si procede fino al ritrovamento di quella corretta.
Possiamo quindi scrivere un metodo che realizzi quanto sopra:
private List<Shikaku> CheckPermutations(List<CellSolutions> shikakus)
{
int rank = shikakus.Count;
if (rank <= 0) return null;
int[] indexes = new int[rank];
int parser = 0;
Shikaku[] solution = new Shikaku[rank];
bool isValid = false;
while (!isValid)
{
solution = new Shikaku[rank];
// Riempio list con la combinazione corrente di shikaku potenziali
for (int i = 0; i < rank; i++)
{
if (indexes[i] > shikakus[i].PotentialSolutions.Count - 1) {
indexes[i] = 0;
++parser;
if (parser >= rank) parser = 0;
}
solution[i] = shikakus[i].PotentialSolutions[indexes[i]];
}
// Verifico se gli elementi inseriti nella soluzione potenziale collidono tra loro
bool collides = true;
for (int i = 0; i < solution.Length; i++)
{
for (int j = 0; j < solution.Length; j++)
{
if (i == j) continue;
collides = IsColliding(solution[i], solution[j]);
if (collides) break;
}
if (collides) break;
}
isValid = !collides;
++indexes[parser++];
if (parser >= rank) parser = 0;
}
return solution.ToList();
}
Come si noterà, il codice è piuttosto semplice. La parte cui prestare maggiore attenzione è ovviamente quella che gestisce il nostro “lucchetto”, qui rappresentato dall'array monodimensionale indexes. Esso conterrà via via tutte le permutazioni di indici da testare, cosa che verrà fatta mediante il metodo IsColliding visto in precedenza. Va da sé che maggiori saranno le caselle valorizzate e le dimensioni dello shikaku, maggiore sarà la complessità risolutiva e le possibilità in gioco (dunque, il tempo necessario ad estrarre la corretta soluzione). Come i metodi evidenziati in precedenza, anche CheckPermutations restituisce un oggetto List<Shikaku>. Quest’ultimo conterrà le singole “diapositive” per ciascuna cella che risulteranno non sovrapposte. In altre parole, ad ogni indice corrisponderà la sua sola soluzione potenziale che non entra in collisione con nessun altro elemento della lista.
Risoluzione dello Shikaku
A questo punto, la risoluzione dello shikaku consta del semplice utilizzo combinato dei metodi fin qui visti.
public void SolveShikaku()
{
this.GetAllSolutions();
var valid = CheckPermutations(this.Solutions);
foreach(var v in valid)
{
v.ConsolePrint();
}
}
La funzione SolveShikaku si occuperà anzitutto di trovare tutte le soluzioni per ciascuna cella tramite GetAllSolutions, per poi eseguire su esse il metodo CheckPermutations e restituire la List<Shikaku> contenente la soluzione. Ciclando su ciascun elemento di essa, potremo produrre – per esempio a video – l’elenco degli shikaku rappresentanti i rettangoli per ciascuna cella a valore.
Il metodo ConsolePrint, scritto proprio per questo scopo, non fa altro che emettere in console il contenuto di uno Shikaku in forma di griglia.
public void ConsolePrint()
{
Console.WriteLine("=====================================================================================");
for(var row =0; row < _SIZE; row++)
{
for(var col = 0; col < _SIZE; col++)
{
Console.Write("{0} ", this.Cells[row, col].ToString("00"));
}
Console.WriteLine();
}
Console.WriteLine("=====================================================================================");
}
Utilizzo e test
Implementata la classe, il suo impiego è semplice. Si consideri ad esempio il seguente snippet:
static Shikaku quadrato = new Shikaku();
quadrato.Cells[0, 2] = 3;
quadrato.Cells[1, 2] = 3;
quadrato.Cells[1, 3] = 2;
quadrato.Cells[1, 4] = 2;
quadrato.Cells[2, 0] = 3;
quadrato.Cells[2, 4] = 2;
quadrato.Cells[3, 0] = 4;
quadrato.Cells[3, 3] = 4;
quadrato.Cells[3, 4] = 2;
quadrato.ConsolePrint();
Console.WriteLine("********************************************************************");
quadrato.SolveShikaku();
Console.Read();
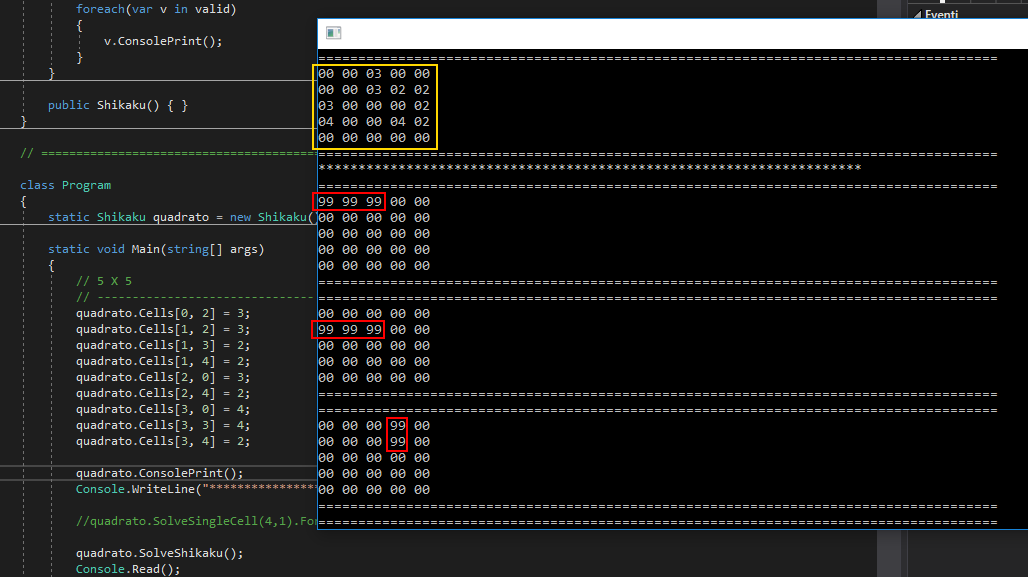
Si procede cioè a definire un oggetto di tipo Shikaku, avendo poi cura di valorizzare le celle iniziali con valori congruenti (ovviamente, tali valori dovranno concorrere ad una griglia risolvibile). Eseguendo il metodo ConsolePrint sull’oggetto così valorizzato, potremo vedere il quadrato originale. Richiamando quindi il metodo SolveShikaku si darà il via alla ricerca dell’unica soluzione valida, e quando essa verrà trovata, verranno visualizzati in console i rettangoli corrispondenti a ciascuna cella.
Nell’esempio sopra, la soluzione viene trovata in circa 3 secondi sulla macchina di test, producendo un output come quello di figura.
Gli ulteriori rettangoli calcolati sono visibili scorrendo la videata di terminale risultante dall'esecuzione dell’esempio.
Codice sorgente
Il sorgente utilizzato in questo articolo è liberamente scaricabile all’indirizzo [https://code.msdn.microsoft.com/C-Permutazioni-nella-41f2592f
](https://code.msdn.microsoft.com/C-Permutazioni-nella-41f2592f)
Altre lingue
Il presente articolo è disponibile anche nelle seguenti localizzazioni: