Trasformazioni matrice in SkiaSharp
Approfondimenti sulle trasformazioni SkiaSharp con la matrice di trasformazione versatile
Tutte le trasformazioni applicate all'oggetto SKCanvas vengono consolidate in una singola istanza della SKMatrix struttura. Si tratta di una matrice di trasformazione standard 3 per 3 simile a quelle in tutti i moderni sistemi grafici 2D.
Come si è visto, è possibile usare le trasformazioni in SkiaSharp senza conoscere la matrice di trasformazione, ma la matrice di trasformazione è importante dal punto di vista teorico ed è fondamentale quando si usano trasformazioni per modificare i percorsi o per gestire l'input tocco complesso, entrambi illustrati in questo articolo e nel successivo.

La matrice di trasformazione corrente applicata a SKCanvas è disponibile in qualsiasi momento accedendo alla proprietà di sola lettura TotalMatrix . È possibile impostare una nuova matrice di trasformazione usando il metodo ed è possibile ripristinare tale SetMatrix matrice in valori predefiniti chiamando ResetMatrix.
L'unico altro SKCanvas membro che funziona direttamente con la trasformazione matrice dell'area di disegno è Concat che concatena due matrici moltiplicandole insieme.
La matrice di trasformazione predefinita è la matrice di identità ed è costituita da 1 nelle celle diagonali e da 0 ovunque:
| 1 0 0 | | 0 1 0 | | 0 0 1 |
È possibile creare una matrice di identità usando il metodo statico SKMatrix.MakeIdentity :
SKMatrix matrix = SKMatrix.MakeIdentity();
Il SKMatrix costruttore predefinito non restituisce una matrice di identità. Restituisce una matrice con tutte le celle impostate su zero. Non usare il SKMatrix costruttore a meno che non si prevede di impostare manualmente tali celle.
Quando SkiaSharp esegue il rendering di un oggetto grafico, ogni punto (x, y) viene convertito in una matrice da 1 a 3 con 1 nella terza colonna:
| x y 1 |
Questa matrice da 1 a 3 rappresenta un punto tridimensionale con la coordinata Z impostata su 1. Esistono motivi matematici (descritti più avanti) perché una trasformazione di matrice bidimensionale richiede il funzionamento in tre dimensioni. Si può pensare a questa matrice da 1 a 3 come che rappresenta un punto in un sistema di coordinate 3D, ma sempre sul piano 2D in cui Z è uguale a 1.
Questa matrice da 1 a 3 viene quindi moltiplicata per la matrice di trasformazione e il risultato è il punto di cui viene eseguito il rendering nell'area di disegno:
| 1 0 0 |
| x y 1 | × | 0 1 0 | = | x' y' z' |
| 0 0 1 |
Usando la moltiplicazione di matrici standard, i punti convertiti sono i seguenti:
x' = x
y' = y
z' = 1
Questa è la trasformazione predefinita.
Quando il Translate metodo viene chiamato sull'oggetto SKCanvas , gli tx argomenti e ty del Translate metodo diventano le prime due celle nella terza riga della matrice di trasformazione:
| 1 0 0 | | 0 1 0 | | tx ty 1 |
La moltiplicazione è ora la seguente:
| 1 0 0 |
| x y 1 | × | 0 1 0 | = | x' y' z' |
| tx ty 1 |
Ecco le formule di trasformazione:
x' = x + tx
y' = y + ty
I fattori di ridimensionamento hanno un valore predefinito pari a 1. Quando si chiama il Scale metodo su un nuovo SKCanvas oggetto, la matrice di trasformazione risultante contiene gli sx argomenti e sy nelle celle diagonali:
| sx 0 0 |
| x y 1 | × | 0 sy 0 | = | x' y' z' |
| 0 0 1 |
Le formule di trasformazione sono le seguenti:
x' = sx · x
y' = sy · y
La matrice di trasformazione dopo la chiamata Skew contiene i due argomenti nelle celle della matrice adiacenti ai fattori di ridimensionamento:
│ 1 ySkew 0 │
| x y 1 | × │ xSkew 1 0 │ = | x' y' z' |
│ 0 0 1 │
Le formule di trasformazione sono:
x' = x + xSkew · y
y' = ySkew · x + y
Per una chiamata a RotateDegrees o RotateRadians per un angolo di α, la matrice di trasformazione è la seguente:
│ cos(α) sin(α) 0 │
| x y 1 | × │ –sin(α) cos(α) 0 │ = | x' y' z' |
│ 0 0 1 │
Ecco le formule di trasformazione:
x' = cos(α) · x - sin(α) · y
y' = sin(α) · x - cos(α) · y
Quando α è di 0 gradi, si tratta della matrice di identità. Quando α è di 180 gradi, la matrice di trasformazione è la seguente:
| –1 0 0 | | 0 –1 0 | | 0 0 1 |
Una rotazione a 180 gradi equivale a capovolgere un oggetto orizzontalmente e verticalmente, che viene eseguito anche impostando i fattori di scala di -1.
Tutti questi tipi di trasformazioni vengono classificati come trasformazioni affine . Le trasformazioni affine non comportano mai la terza colonna della matrice, che rimane ai valori predefiniti 0, 0 e 1. L'articolo Trasformazioni non affine illustra le trasformazioni non affine.
Moltiplicazione di matrici
Un vantaggio significativo con l'uso della matrice di trasformazione è che le trasformazioni composite possono essere ottenute dalla moltiplicazione di matrici, spesso indicate nella documentazione di SkiaSharp come concatenazione. Molti dei metodi correlati alla trasformazione in SKCanvas fanno riferimento a "pre-concatenazione" o "pre-concat". Questo si riferisce all'ordine di moltiplicazione, che è importante perché la moltiplicazione della matrice non è commutativa.
Ad esempio, la documentazione per il Translate metodo indica che "pre-concatse la matrice corrente con la traduzione specificata", mentre la documentazione per il Scale metodo indica che "Pre-concatse la matrice corrente con la scala specificata".
Ciò significa che la trasformazione specificata dalla chiamata al metodo è il moltiplicatore (l'operando a sinistra) e la matrice di trasformazione corrente è il moltiplicatore (l'operando di destra).
Si supponga che Translate venga chiamato seguito da Scale:
canvas.Translate(tx, ty);
canvas.Scale(sx, sy);
La Scale trasformazione viene moltiplicata per la Translate trasformazione per la matrice di trasformazione composita:
| sx 0 0 | | 1 0 0 | | sx 0 0 | | 0 sy 0 | × | 0 1 0 | = | 0 sy 0 | | 0 0 1 | | tx ty 1 | | tx ty 1 |
Scale potrebbe essere chiamato prima Translate come segue:
canvas.Scale(sx, sy);
canvas.Translate(tx, ty);
In tal caso, l'ordine della moltiplicazione viene invertito e i fattori di ridimensionamento vengono applicati efficacemente ai fattori di traslazione:
| 1 0 0 | | sx 0 0 | | sx 0 0 | | 0 1 0 | × | 0 sy 0 | = | 0 sy 0 | | tx ty 1 | | 0 0 1 | | tx·sx ty·sy 1 |
Ecco il Scale metodo con un punto pivot:
canvas.Scale(sx, sy, px, py);
Equivale alle chiamate di conversione e scalabilità seguenti:
canvas.Translate(px, py);
canvas.Scale(sx, sy);
canvas.Translate(–px, –py);
Le tre matrici di trasformazione vengono moltiplicate in ordine inverso rispetto alla modalità di visualizzazione dei metodi nel codice:
| 1 0 0 | | sx 0 0 | | 1 0 0 | | sx 0 0 | | 0 1 0 | × | 0 sy 0 | × | 0 1 0 | = | 0 sy 0 | | –px –py 1 | | 0 0 1 | | px py 1 | | px–px·sx py–py·sy 1 |
Struttura SKMatrix
La SKMatrix struttura definisce nove proprietà di lettura/scrittura di tipo float corrispondenti alle nove celle della matrice di trasformazione:
│ ScaleX SkewY Persp0 │ │ SkewX ScaleY Persp1 │ │ TransX TransY Persp2 │
SKMatrix definisce anche una proprietà denominata Values di tipo float[]. Questa proprietà può essere usata per impostare o ottenere i nove valori in un'unica ripresa nell'ordine ScaleX, SkewXTransX, SkewY, ScaleY, TransYPersp0, Persp1, , e Persp2.
Le Persp0celle , Persp1e Persp2 sono descritte nell'articolo Trasformazioni non affine. Se queste celle hanno i valori predefiniti 0, 0 e 1, la trasformazione viene moltiplicata per un punto di coordinate simile al seguente:
│ ScaleX SkewY 0 │
| x y 1 | × │ SkewX ScaleY 0 │ = | x' y' z' |
│ TransX TransY 1 │
x' = ScaleX · x + SkewX · y + TransX
y' = SkewX · x + ScaleY · y + TransY
z' = 1
Questa è la trasformazione affine bidimensionale completa. La trasformazione affine mantiene le linee parallele, il che significa che un rettangolo non viene mai trasformato in qualcosa di diverso da un parallelogramma.
La SKMatrix struttura definisce diversi metodi statici per creare SKMatrix valori. Tutti questi valori restituiscono SKMatrix :
MakeTranslationMakeScaleMakeScalecon un punto pivotMakeRotationper un angolo in radiantiMakeRotationper un angolo in radianti con un punto pivotMakeRotationDegreesMakeRotationDegreescon un punto pivotMakeSkew
SKMatrix definisce anche diversi metodi statici che concatenano due matrici, ovvero moltiplicarle. Questi metodi sono denominati Concat, PostConcate PreConcate sono disponibili due versioni di ognuna. Questi metodi non hanno valori restituiti; fanno invece riferimento ai valori esistenti SKMatrix tramite ref argomenti. Nell'esempio seguente, A, Be R (per "result") sono tutti valori SKMatrix .
I due Concat metodi vengono chiamati come segue:
SKMatrix.Concat(ref R, A, B);
SKMatrix.Concat(ref R, ref A, ref B);
Queste operazioni eseguono la moltiplicazione seguente:
R = B × A
Gli altri metodi hanno solo due parametri. Il primo parametro viene modificato e, in caso di restituzione dalla chiamata al metodo, contiene il prodotto delle due matrici. I due PostConcat metodi vengono chiamati come segue:
SKMatrix.PostConcat(ref A, B);
SKMatrix.PostConcat(ref A, ref B);
Queste chiamate eseguono l'operazione seguente:
A = A × B
I due PreConcat metodi sono simili:
SKMatrix.PreConcat(ref A, B);
SKMatrix.PreConcat(ref A, ref B);
Queste chiamate eseguono l'operazione seguente:
A = B × A
Le versioni di questi metodi con tutti gli ref argomenti sono leggermente più efficienti per chiamare le implementazioni sottostanti, ma potrebbe generare confusione con un utente che legge il codice e presupponendo che qualsiasi elemento con un ref argomento venga modificato dal metodo . Inoltre, è spesso utile passare un argomento che è il risultato di uno dei Make metodi, ad esempio:
SKMatrix result;
SKMatrix.Concat(result, SKMatrix.MakeTranslation(100, 100),
SKMatrix.MakeScale(3, 3));
Verrà creata la matrice seguente:
│ 3 0 0 │ │ 0 3 0 │ │ 100 100 1 │
Si tratta della trasformazione di scala moltiplicata per la trasformazione traslazione. In questo caso specifico, la SKMatrix struttura fornisce un collegamento con un metodo denominato SetScaleTranslate:
SKMatrix R = new SKMatrix();
R.SetScaleTranslate(3, 3, 100, 100);
Questo è uno dei pochi casi in cui è sicuro usare il SKMatrix costruttore. Il SetScaleTranslate metodo imposta tutte e nove le celle della matrice. È anche possibile usare il SKMatrix costruttore con i metodi e RotateDegrees staticiRotate:
SKMatrix R = new SKMatrix();
SKMatrix.Rotate(ref R, radians);
SKMatrix.Rotate(ref R, radians, px, py);
SKMatrix.RotateDegrees(ref R, degrees);
SKMatrix.RotateDegrees(ref R, degrees, px, py);
Questi metodi non concatenano una trasformazione di rotazione in una trasformazione esistente. I metodi impostano tutte le celle della matrice. Sono funzionalmente identici ai MakeRotation metodi e MakeRotationDegrees , ad eccezione del fatto che non creano un'istanza del SKMatrix valore.
Si supponga di avere un SKPath oggetto che si desidera visualizzare, ma si preferisce che abbia un orientamento leggermente diverso o un punto centrale diverso. È possibile modificare tutte le coordinate di tale percorso chiamando il Transform metodo di SKPath con un SKMatrix argomento . La pagina Trasformazione percorso illustra come eseguire questa operazione. La PathTransform classe fa riferimento all'oggetto HendecagramPath in un campo, ma usa il relativo costruttore per applicare una trasformazione a tale percorso:
public class PathTransformPage : ContentPage
{
SKPath transformedPath = HendecagramArrayPage.HendecagramPath;
public PathTransformPage()
{
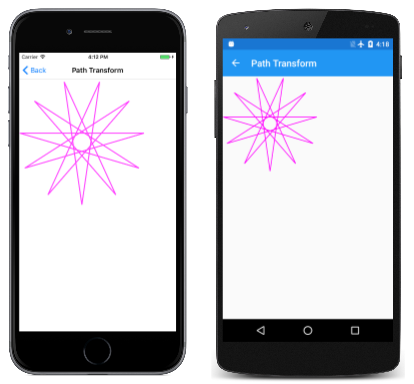
Title = "Path Transform";
SKCanvasView canvasView = new SKCanvasView();
canvasView.PaintSurface += OnCanvasViewPaintSurface;
Content = canvasView;
SKMatrix matrix = SKMatrix.MakeScale(3, 3);
SKMatrix.PostConcat(ref matrix, SKMatrix.MakeRotationDegrees(360f / 22));
SKMatrix.PostConcat(ref matrix, SKMatrix.MakeTranslation(300, 300));
transformedPath.Transform(matrix);
}
...
}
L'oggetto HendecagramPath ha un centro a (0, 0) e i 11 punti della stella si estendono verso l'esterno da quel centro di 100 unità in tutte le direzioni. Ciò significa che il percorso ha coordinate positive e negative. La pagina Trasformazione percorso preferisce lavorare con una stella tre volte più grande e con tutte le coordinate positive. Inoltre, non vuole che un punto della stella punti dritto verso l'alto. Vuole invece che un punto della stella punti dritto verso il basso. Poiché la stella ha 11 punti, non può avere entrambi. Ciò richiede la rotazione della stella di 360 gradi diviso per 22.
Il costruttore compila un SKMatrix oggetto da tre trasformazioni separate usando il metodo con il PostConcat modello seguente, dove A, B e C sono istanze di SKMatrix:
SKMatrix matrix = A;
SKMatrix.PostConcat(ref A, B);
SKMatrix.PostConcat(ref A, C);
Si tratta di una serie di moltiplicazioni successive, quindi il risultato è il seguente:
A × B × C
Le moltiplicazioni consecutive aiutano a comprendere le operazioni che ogni trasformazione esegue. La trasformazione della scala aumenta le dimensioni delle coordinate del percorso di un fattore pari a 3, quindi le coordinate vanno da -300 a 300. La trasformazione ruota ruota la stella intorno all'origine. La trasformazione di traslazione lo sposta quindi di 300 pixel verso destra e giù, in modo che tutte le coordinate diventino positive.
Esistono altre sequenze che producono la stessa matrice. Ecco un altro:
SKMatrix matrix = SKMatrix.MakeRotationDegrees(360f / 22);
SKMatrix.PostConcat(ref matrix, SKMatrix.MakeTranslation(100, 100));
SKMatrix.PostConcat(ref matrix, SKMatrix.MakeScale(3, 3));
In questo modo il percorso viene ruotato intorno al centro, quindi lo converte 100 pixel a destra e verso il basso in modo che tutte le coordinate siano positive. La stella viene quindi aumentata di dimensioni rispetto al nuovo angolo superiore sinistro, ovvero il punto (0, 0).
Il gestore può semplicemente eseguire il PaintSurface rendering di questo percorso:
public class PathTransformPage : ContentPage
{
...
void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
SKImageInfo info = args.Info;
SKSurface surface = args.Surface;
SKCanvas canvas = surface.Canvas;
canvas.Clear();
using (SKPaint paint = new SKPaint())
{
paint.Style = SKPaintStyle.Stroke;
paint.Color = SKColors.Magenta;
paint.StrokeWidth = 5;
canvas.DrawPath(transformedPath, paint);
}
}
}
Viene visualizzato nell'angolo superiore sinistro dell'area di disegno:
Il costruttore di questo programma applica la matrice al percorso con la chiamata seguente:
transformedPath.Transform(matrix);
Il percorso non mantiene questa matrice come proprietà. Applica invece la trasformazione a tutte le coordinate del percorso. Se Transform viene chiamato di nuovo, la trasformazione viene nuovamente applicata e l'unico modo in cui è possibile tornare indietro consiste nell'applicare un'altra matrice che annulla la trasformazione. Fortunatamente, la SKMatrix struttura definisce un TryInvert metodo che ottiene la matrice che inverte una determinata matrice:
SKMatrix inverse;
bool success = matrix.TryInverse(out inverse);
Il metodo viene chiamato TryInverse perché non tutte le matrici sono invertibili, ma è probabile che non venga usata una matrice non invertibile per una trasformazione grafica.
È anche possibile applicare una trasformazione matrice a un SKPoint valore, una matrice di punti, un SKRectoggetto o anche un solo numero all'interno del programma. La SKMatrix struttura supporta queste operazioni con una raccolta di metodi che iniziano con la parola Map, ad esempio:
SKPoint transformedPoint = matrix.MapPoint(point);
SKPoint transformedPoint = matrix.MapPoint(x, y);
SKPoint[] transformedPoints = matrix.MapPoints(pointArray);
float transformedValue = matrix.MapRadius(floatValue);
SKRect transformedRect = matrix.MapRect(rect);
Se si usa l'ultimo metodo, tenere presente che la SKRect struttura non è in grado di rappresentare un rettangolo ruotato. Il metodo ha senso solo per un SKMatrix valore che rappresenta la conversione e la scalabilità.
Sperimentazione interattiva
Un modo per ottenere un'impressione per la trasformazione affine consiste nello spostamento interattivo di tre angoli di una bitmap intorno allo schermo e la visualizzazione dei risultati della trasformazione. Questa è l'idea alla base della pagina Mostra matrice affine. Questa pagina richiede altre due classi usate anche in altre dimostrazioni:
La TouchPoint classe visualizza un cerchio traslucente che può essere trascinato intorno allo schermo. TouchPoint richiede che un SKCanvasView elemento o che sia un elemento padre di un oggetto SKCanvasView associato TouchEffect . Impostare la proprietà Capture su true. TouchAction Nel gestore eventi, il programma deve chiamare il ProcessTouchEvent metodo in TouchPoint per ogni TouchPoint istanza. Il metodo restituisce true se l'evento di tocco ha causato lo spostamento del punto di tocco. Inoltre, il PaintSurface gestore deve chiamare il Paint metodo in ogni TouchPoint istanza, passandolo all'oggetto SKCanvas .
TouchPoint illustra un modo comune in cui un oggetto visivo SkiaSharp può essere incapsulato in una classe separata. La classe può definire proprietà per specificare le caratteristiche dell'oggetto visivo e un metodo denominato Paint con un SKCanvas argomento può eseguirne il rendering.
La Center proprietà di TouchPoint indica la posizione dell'oggetto . Questa proprietà può essere impostata per inizializzare la posizione; la proprietà cambia quando l'utente trascina il cerchio intorno all'area di disegno.
Anche la pagina Show Affine Matrix (Mostra matrice affine) richiede la MatrixDisplay classe . Questa classe visualizza le celle di un SKMatrix oggetto . Dispone di due metodi pubblici: Measure per ottenere le dimensioni della matrice sottoposta a rendering e Paint per visualizzarla. La classe contiene una MatrixPaint proprietà di tipo SKPaint che può essere sostituita per una dimensione o un colore del carattere diversi.
Il file ShowAffineMatrixPage.xaml crea un'istanza di SKCanvasView e allega un oggetto TouchEffect. Il file code-behind ShowAffineMatrixPage.xaml.cs crea tre TouchPoint oggetti e li imposta su posizioni corrispondenti a tre angoli di una bitmap caricata da una risorsa incorporata:
public partial class ShowAffineMatrixPage : ContentPage
{
SKMatrix matrix;
SKBitmap bitmap;
SKSize bitmapSize;
TouchPoint[] touchPoints = new TouchPoint[3];
MatrixDisplay matrixDisplay = new MatrixDisplay();
public ShowAffineMatrixPage()
{
InitializeComponent();
string resourceID = "SkiaSharpFormsDemos.Media.SeatedMonkey.jpg";
Assembly assembly = GetType().GetTypeInfo().Assembly;
using (Stream stream = assembly.GetManifestResourceStream(resourceID))
{
bitmap = SKBitmap.Decode(stream);
}
touchPoints[0] = new TouchPoint(100, 100); // upper-left corner
touchPoints[1] = new TouchPoint(bitmap.Width + 100, 100); // upper-right corner
touchPoints[2] = new TouchPoint(100, bitmap.Height + 100); // lower-left corner
bitmapSize = new SKSize(bitmap.Width, bitmap.Height);
matrix = ComputeMatrix(bitmapSize, touchPoints[0].Center,
touchPoints[1].Center,
touchPoints[2].Center);
}
...
}
Una matrice affine è definita in modo univoco da tre punti. I tre TouchPoint oggetti corrispondono agli angoli superiore sinistro, superiore destro e inferiore sinistro della bitmap. Poiché una matrice affine è in grado di trasformare un rettangolo in un parallelogramma, il quarto punto è implicito dagli altri tre. Il costruttore termina con una chiamata a ComputeMatrix, che calcola le celle di un SKMatrix oggetto da questi tre punti.
Il TouchAction gestore chiama il ProcessTouchEvent metodo di ogni TouchPointoggetto . Il scale valore converte da Xamarin.Forms coordinate a pixel:
public partial class ShowAffineMatrixPage : ContentPage
{
...
void OnTouchEffectAction(object sender, TouchActionEventArgs args)
{
bool touchPointMoved = false;
foreach (TouchPoint touchPoint in touchPoints)
{
float scale = canvasView.CanvasSize.Width / (float)canvasView.Width;
SKPoint point = new SKPoint(scale * (float)args.Location.X,
scale * (float)args.Location.Y);
touchPointMoved |= touchPoint.ProcessTouchEvent(args.Id, args.Type, point);
}
if (touchPointMoved)
{
matrix = ComputeMatrix(bitmapSize, touchPoints[0].Center,
touchPoints[1].Center,
touchPoints[2].Center);
canvasView.InvalidateSurface();
}
}
...
}
Se è TouchPoint stato spostato, il metodo chiama ComputeMatrix nuovamente e invalida la superficie.
Il ComputeMatrix metodo determina la matrice implicita da questi tre punti. La matrice denominata A trasforma un rettangolo quadrato di un pixel in un parallelogramma basato sui tre punti, mentre la trasformazione di scala denominata S ridimensiona la bitmap in un rettangolo quadrato di un pixel. La matrice composita è S × A:
public partial class ShowAffineMatrixPage : ContentPage
{
...
static SKMatrix ComputeMatrix(SKSize size, SKPoint ptUL, SKPoint ptUR, SKPoint ptLL)
{
// Scale transform
SKMatrix S = SKMatrix.MakeScale(1 / size.Width, 1 / size.Height);
// Affine transform
SKMatrix A = new SKMatrix
{
ScaleX = ptUR.X - ptUL.X,
SkewY = ptUR.Y - ptUL.Y,
SkewX = ptLL.X - ptUL.X,
ScaleY = ptLL.Y - ptUL.Y,
TransX = ptUL.X,
TransY = ptUL.Y,
Persp2 = 1
};
SKMatrix result = SKMatrix.MakeIdentity();
SKMatrix.Concat(ref result, A, S);
return result;
}
...
}
Infine, il metodo esegue il PaintSurface rendering della bitmap in base a tale matrice, visualizza la matrice nella parte inferiore dello schermo ed esegue il rendering dei punti di tocco nei tre angoli della bitmap:
public partial class ShowAffineMatrixPage : ContentPage
{
...
void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
SKImageInfo info = args.Info;
SKSurface surface = args.Surface;
SKCanvas canvas = surface.Canvas;
canvas.Clear();
// Display the bitmap using the matrix
canvas.Save();
canvas.SetMatrix(matrix);
canvas.DrawBitmap(bitmap, 0, 0);
canvas.Restore();
// Display the matrix in the lower-right corner
SKSize matrixSize = matrixDisplay.Measure(matrix);
matrixDisplay.Paint(canvas, matrix,
new SKPoint(info.Width - matrixSize.Width,
info.Height - matrixSize.Height));
// Display the touchpoints
foreach (TouchPoint touchPoint in touchPoints)
{
touchPoint.Paint(canvas);
}
}
}
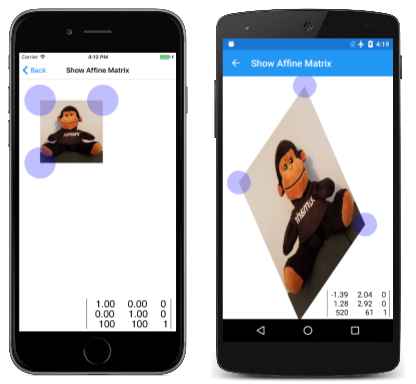
La schermata iOS seguente mostra la bitmap al primo caricamento della pagina, mentre le altre due schermate lo mostrano dopo alcune modifiche:
Anche se sembra che i punti di tocco trascinano gli angoli della bitmap, questa è solo un'illusione. La matrice calcolata dai punti di tocco trasforma la bitmap in modo che gli angoli coincidano con i punti di tocco.
È più naturale per gli utenti spostare, ridimensionare e ruotare bitmap non trascinando gli angoli, ma usando una o due dita direttamente sull'oggetto per trascinare, avvicinare e ruotare. Questo argomento è illustrato nell'articolo successivo Manipolazione del tocco.
Motivo della matrice da 3 a 3
Potrebbe essere previsto che un sistema di grafica bidimensionale richieda solo una matrice di trasformazione 2 per 2:
│ ScaleX SkewY │
| x y | × │ │ = | x' y' |
│ SkewX ScaleY │
Questo funziona per ridimensionamento, rotazione e anche asimmetria, ma non è in grado di eseguire le trasformazioni più semplici, ovvero la traslazione.
Il problema è che la matrice 2 per 2 rappresenta una trasformazione lineare in due dimensioni. Una trasformazione lineare mantiene alcune operazioni aritmetiche di base, ma una delle implicazioni è che una trasformazione lineare non modifica mai il punto (0, 0). Una trasformazione lineare rende impossibile la traduzione.
In tre dimensioni, una matrice di trasformazione lineare è simile alla seguente:
│ ScaleX SkewYX SkewZX │
| x y z | × │ SkewXY ScaleY SkewZY │ = | x' y' z' |
│ SkewXZ SkewYZ ScaleZ │
La cella etichettata SkewXY indica che il valore inclina la coordinata X in base ai valori di Y. La cella SkewXZ indica che il valore inclina la coordinata X in base ai valori di Z e i valori si asimmetriano in modo analogo per le altre Skew celle.
È possibile limitare questa matrice di trasformazione 3D a un piano bidimensionale impostando e SkewZY su SkewZX 0 e ScaleZ su 1:
│ ScaleX SkewYX 0 │
| x y z | × │ SkewXY ScaleY 0 │ = | x' y' z' |
│ SkewXZ SkewYZ 1 │
Se la grafica bidimensionale viene disegnata interamente sul piano nello spazio 3D in cui Z è uguale a 1, la moltiplicazione della trasformazione è simile alla seguente:
│ ScaleX SkewYX 0 │
| x y 1 | × │ SkewXY ScaleY 0 │ = | x' y' 1 |
│ SkewXZ SkewYZ 1 │
Tutto rimane sul piano bidimensionale dove Z è uguale a 1, ma le SkewXZ celle e SkewYZ diventano effettivamente fattori di traslazione bidimensionale.
Questo è il modo in cui una trasformazione lineare tridimensionale funge da trasformazione non lineare bidimensionale. (Per analogia, le trasformazioni nella grafica 3D sono basate su una matrice da 4 a 4).
La SKMatrix struttura in SkiaSharp definisce le proprietà per la terza riga:
│ ScaleX SkewY Persp0 │
| x y 1 | × │ SkewX ScaleY Persp1 │ = | x' y' z` |
│ TransX TransY Persp2 │
Valori diversi da zero di Persp0 e Persp1 comportano trasformazioni che spostano gli oggetti dal piano bidimensionale in cui Z è uguale a 1. Cosa accade quando questi oggetti vengono spostati di nuovo in tale piano è illustrato nell'articolo sulle trasformazioni non affine.