Appendice: Trasformazioni matrice

Questo argomento fornisce una panoramica matematica delle trasformazioni di matrice per la grafica 2D. Tuttavia, non è necessario conoscere la matematica della matrice per usare le trasformazioni in Direct2D. Leggere questo argomento se si è interessati alla matematica; in caso contrario, è possibile ignorare questo argomento.

• Introduzione alle matrici
  • Operazioni matrice
• Trasformazioni affine
  • Trasformazione traduzione
  • Ridimensionamento della trasformazione
  • Rotazione intorno all'origine
  • Rotazione intorno a un punto arbitrario
  • Trasformazione asimmetria
• Rappresentazione di trasformazioni in Direct2D
• Avanti

Introduzione alle matrici

Una matrice è una matrice rettangolare di numeri reali. L'ordine della matrice è il numero di righe e colonne. Ad esempio, se la matrice contiene 3 righe e 2 colonne, l'ordine è 3 × 2. Le matrici vengono in genere visualizzate con gli elementi matrice racchiusi tra parentesi quadre:

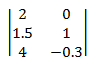
Notazione: una matrice è designata da una lettera maiuscola. Gli elementi sono designati da lettere minuscole. I pedice indicano il numero di riga e colonna di un elemento. Ad esempio, unij è l'elemento nella colonna i'th e j'th della matrice A.

Il diagramma seguente mostra una matrice i × j, con i singoli elementi in ogni cella della matrice.

Operazioni matrice

In questa sezione vengono descritte le operazioni di base definite sulle matrici.

Addizione. La somma A + B di due matrici viene ottenuta aggiungendo gli elementi corrispondenti di A e B:

A + B = \[ a*ij* \] + \[ b*ij* \] = \[ a*ij* + b*ij* \]

Moltiplicazione scalare. Questa operazione moltiplica una matrice per un numero reale. Dato un numero reale k, il prodotto scalare kA viene ottenuto moltiplicando ogni elemento di A per k.

kA = k\[ a*ij* \] = \[ k × a*ij* \]

Moltiplicazione della matrice. Date due matrici A e B con ordine (m × n) e (n × p), il prodotto C = A × B è una matrice con ordine (m × p), definito come segue:

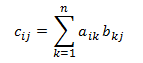
oppure, in modo equivalente:

c*ij* = a*i*1 x b1*j* + a*i*2 x b2*j* + ... + a*in* + b*nj*

Ovvero, per calcolare ogni elemento cij, eseguire le operazioni seguenti:

1. Prendi la i'th riga di A e la colonna j'th di B.
2. Moltiplicare ogni coppia di elementi nella riga e nella colonna: la prima voce di riga per la prima voce di colonna, la seconda voce di riga per la seconda voce di colonna e così via.
3. Sommare il risultato.

Di seguito è riportato un esempio di moltiplicazione di una matrice (2 × 2) per una matrice (2 × 3).

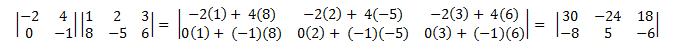
La moltiplicazione della matrice non è commutativa. Ovvero, A × B ≠ B × A. Inoltre, dalla definizione segue che non tutte le coppie di matrici possono essere moltiplicate. Il numero di colonne nella matrice a sinistra deve essere uguale al numero di righe nella matrice di destra. In caso contrario, l'operatore × non è definito.

Identificare la matrice. Una matrice di identità, designata I, è una matrice quadrata definita come segue:

I*ij* = 1 se *i* = *j*, o 0 in caso contrario.

In altre parole, una matrice identity contiene 1 per ogni elemento in cui il numero di riga è uguale al numero di colonna e zero per tutti gli altri elementi. Ad esempio, ecco la matrice di identità 3 × 3.

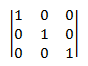
Il blocco di uguaglianza seguente per qualsiasi matrice M.

M x I = M I x M = M

Trasformazioni affine

Una trasformazione affine è un'operazione matematica che esegue il mapping di uno spazio di coordinate a un altro. In altre parole, esegue il mapping di un set di punti a un altro set di punti. Le trasformazioni affine hanno alcune funzionalità che li rendono utili nella grafica computer.

• Le trasformazioni affine mantengono la collinearità. Se tre o più punti rientrano in una linea, formano comunque una linea dopo la trasformazione. Le linee rette rimangono dritte.
• La composizione di due trasformazioni affine è una trasformazione affine.

Le trasformazioni affine per lo spazio 2D hanno il formato seguente.

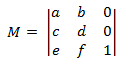
Se si applica la definizione della moltiplicazione della matrice specificata in precedenza, è possibile indicare che il prodotto di due trasformazioni affine è un'altra trasformazione affine. Per trasformare un punto 2D usando una trasformazione affine, il punto viene rappresentato come matrice 1 × 3.

P = \| x y 1 \|

I primi due elementi contengono le coordinate x e y del punto. Il 1 viene inserito nel terzo elemento per fare in modo che la matematica funzioni correttamente. Per applicare la trasformazione, moltiplicare le due matrici come indicato di seguito.

P' = P × M

Viene espansa fino a quanto segue.

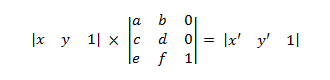
dove

x' = ax + cy + e y' = bx + dy + f

Per ottenere il punto trasformato, prendere i primi due elementi della matrice P'.

p = (x', y') = (ax + cy + e, bx + dy + f)

Le sezioni successive derivano le trasformazioni di base.

Trasformazione traduzione

La matrice di trasformazione traslazione ha il formato seguente.

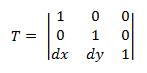
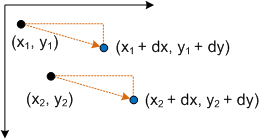
Collegare un punto P in questa equazione restituisce:

P' = (*x* + *dx*, *y* + *dy*)

che corrisponde al punto (x, y) convertito da dx nell'asse X e dy nell'asse Y.

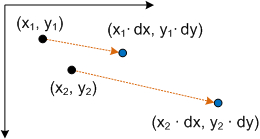
Ridimensionamento della trasformazione

La matrice di trasformazione del ridimensionamento ha il formato seguente.

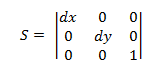
Collegare un punto P a questa equazione restituisce:

P' = (*x* (*) *dx*, *y* * * *dy*)

che corrisponde al punto (x,y) ridimensionato da dx e dy.

Rotazione intorno all'origine

La matrice per ruotare un punto intorno all'origine ha il formato seguente.

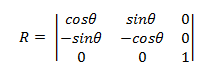
Il punto trasformato è:

P' = (*x*cosΘ – ysinΘ, *x*sinΘ + *y*cosΘ)

Prova. Per mostrare che P' rappresenta una rotazione, prendere in considerazione il diagramma seguente.

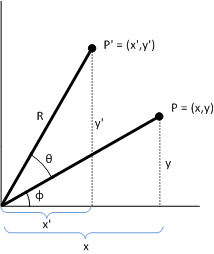
Si consideri quanto segue:

P = (x,y)

Punto originale da trasformare.

Φ

Angolo formato dalla linea (0,0) a P.

Θ

Angolo da cui ruotare (x,y) sull'origine.

P' = (x',y')

Punto trasformato.

R

Lunghezza della linea (0,0) a P. Inoltre il raggio del cerchio di rotazione.

L'angolo tra l'asse x e la linea (0,0) a P' è Γ + Θ. Le identità seguenti contengono:

x = R cosΓ y = R sinΓ x' = R cos(Γ + Θ) y' = R sin(Γ+ Θ)

Ora risolvere per x' e y' in termini di Θ. Per le formule di addizione trigonometriche:

x' = R(cosΓcosΘ – sinΓsinΘ) = RcosΓcosΘ – RsinΓsinΘ y' = R(sinΓcosΘ + cosΓsinΘ) = RsinΓcosΘ + RcosΓsinΘ

Sostituendo, si ottiene:

x' = xcosΘ – ysinΘ y' = xsinΘ + ycosΘ

che corrisponde al punto trasformato P' illustrato in precedenza.

Rotazione intorno a un punto arbitrario

Per ruotare intorno a un punto (x,y) diverso dall'origine, viene usata la matrice seguente.

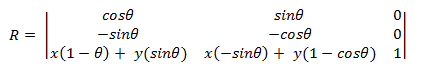
È possibile derivare questa matrice prendendo il punto (x,y) per essere l'origine.

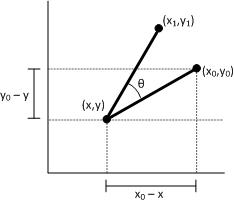
Let (x1, y1) essere il punto che determina la rotazione del punto (x0, y0) intorno al punto (x,y). È possibile derivare x1 come indicato di seguito.

x1 = (x0 – x)cosΘ – (y0 – y)sinΘ + x x1 = x0cosΘ – y0sinΘ + \[ (1 – cosΘ) + ysinΘ \]

Collegare ora questa equazione alla matrice di trasformazione usando la formula x1 = ax0 + cy0 + e da precedenza. Usare la stessa procedura per derivare y1.

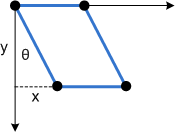
Trasformazione asimmetria

La trasformazione asimmetria è definita da quattro parametri:

• Θ: quantità di inclinazione lungo l'asse x, misurata come angolo dall'asse y.
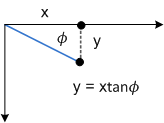
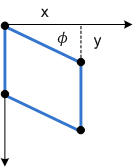
• Φ: la quantità di inclinazione lungo l'asse y, misurata come angolo dall'asse x.
• (px, py): le coordinate x e y del punto su cui viene eseguita l'asimmetria.

La trasformazione asimmetria usa la matrice seguente.

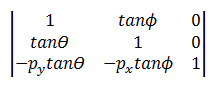
Il punto trasformato è:

P' = (*x* + *y*tanΘ – *py*tanΘ, *y* + *x*tanΓ) – *py*tanΓ

o equivalentemente:

P' = (*x* + (*y* – *py*)tanΘ, *y* + (*x* – *px*)tanΓ)

Per vedere come funziona questa trasformazione, considerare singolarmente ogni componente. Il parametro Θ sposta ogni punto nella direzione x in base a un importo uguale a tanΘ. Il diagramma seguente mostra la relazione tra Θ e l'asse x.

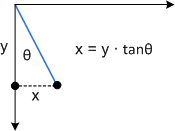
Ecco la stessa deviazione applicata a un rettangolo:

Il parametro Φ ha lo stesso effetto, ma lungo l'asse y:

Il diagramma successivo mostra l'asimmetria dell'asse y applicata a un rettangolo.

Infine, i parametri px e py spostano il punto centrale per l'asimmetria lungo gli assi x- e y.

Rappresentazione delle trasformazioni in Direct2D

Tutte le trasformazioni Direct2D sono trasformazioni affine. Direct2D non supporta trasformazioni non affine. Le trasformazioni sono rappresentate dalla struttura D2D1_MATRIX_3X2_F . Questa struttura definisce una matrice di 3 × 2. Poiché la terza colonna di una trasformazione affine è sempre la stessa ([0, 0, 1]), e poiché Direct2D non supporta trasformazioni non affine, non è necessario specificare l'intera matrice 3 × 3. Internamente, Direct2D usa 3 matrici × 3 per calcolare le trasformazioni.

I membri della D2D1_MATRIX_3X2_F sono denominati in base alla posizione dell'indice: il membro _11 è elemento (1,1), il membro _12 è l'elemento (1,2) e così via. Anche se è possibile inizializzare direttamente i membri della struttura, è consigliabile usare la classe D2D1::Matrix3x2F . Questa classe eredita D2D1_MATRIX_3X2_F e fornisce metodi helper per la creazione di una delle trasformazioni di affine di base. La classe definisce anche operator*() per la composizione di due o più trasformazioni, come descritto in Applica trasformazioni in Direct2D.

Prossima

Modulo 4. Input utente