series_fit_poly()
適用対象: ✅Microsoft Fabric✅Azure データ エクスプローラー✅Azure Monitor✅Microsoft Sentinel
独立変数 (x_series) から従属変数 (y_series) への多項式回帰を適用します。 この関数は、複数の系列 (動的な数値配列) を含むテーブルを受け取り、多項式回帰を使用して各系列に最適な高次多項式を生成します。
ヒント
- make-series 演算子によって作成されるような等間隔の系列について線形回帰を行う場合は、よりシンプルな関数 series_fit_line() を使用してください。 「例 2」を参照してください。
- x_series を指定して回帰を高次で実行する場合は、[0 ~ 1] の範囲に正規化することを検討してください。 「例 3」を参照してください。
- x_series が datetime 型でない場合は、double 型に変換して正規化する必要があります。 「例 3」を参照してください。
- インライン Python を使用した多項式回帰のリファレンス実装については、「series_fit_poly_fl()」を参照してください。
構文
T | extend series_fit_poly(y_series [, x_series, degree ])
構文規則について詳しく知る。
パラメーター
| 件名 | タイプ | Required | 説明 |
|---|---|---|---|
| y_series | dynamic |
✔️ | 依存変数を含む数値の配列。 |
| x_series | dynamic |
independent 変数を含む数値の配列。 系列が等間隔ではない場合のみ必要です。 指定しない場合は、既定値 [1, 2, ..., length(y_series)]に設定されます。 | |
| degree | 適合に使用する多項式の次数。 たとえば、線形回帰の場合は 1、二次回帰の場合は 2、などとなります。 既定値は 1 で、線形回帰を示します。 |
返品
series_fit_poly() 関数は次の列を返します。
rsquare: 決定係数は、適合度の標準的な測定方法です。 値は [0-1] の範囲の数値です。1 は適合度が最も高いことを表し、0 はデータが順序付けされておらず、どの直線にも適合しないことを意味します。coefficients: 指定された次数において最良適合となる多項式の係数を、指数の大きさ順に保持する数値配列。variance: 従属変数 (y_series) の分散。rvariance: 入力データの値と近似値との差を示す残差分散。poly_fit: 最も適合する多項式の値の系列を保持する数値配列。 系列の長さは従属変数 (y_series) の長さと同じです。 この値はグラフ作成に使用します。
例
例 1
x 軸と y 軸のノイズを含む 5 次多項式:
range x from 1 to 200 step 1
| project x = rand()*5 - 2.3
| extend y = pow(x, 5)-8*pow(x, 3)+10*x+6
| extend y = y + (rand() - 0.5)*0.5*y
| summarize x=make_list(x), y=make_list(y)
| extend series_fit_poly(y, x, 5)
| project-rename fy=series_fit_poly_y_poly_fit, coeff=series_fit_poly_y_coefficients
|fork (project x, y, fy) (project-away x, y, fy)
| render linechart
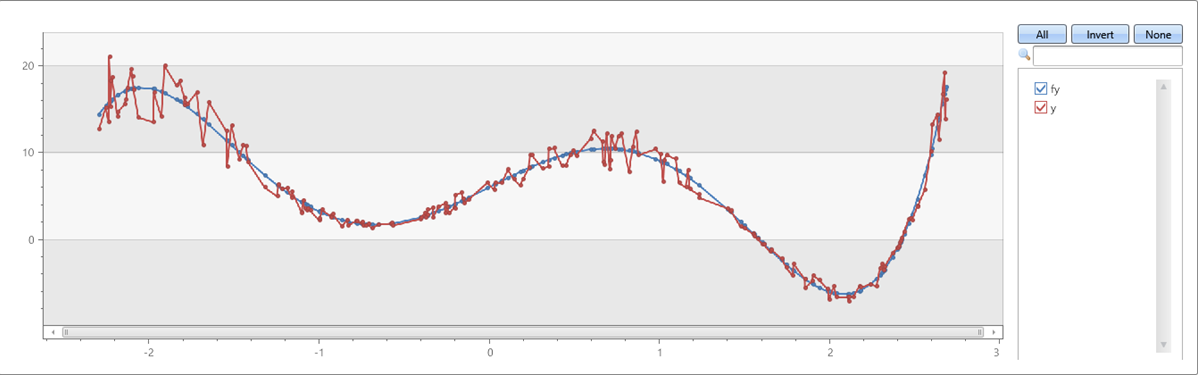
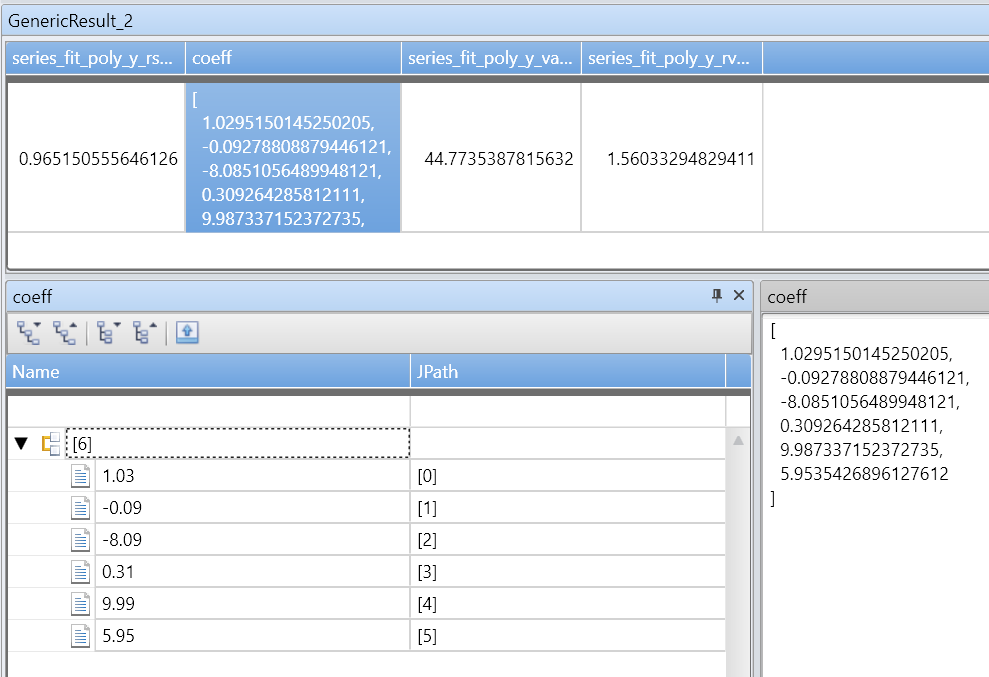
例 2
degree が 1 の series_fit_poly が series_fit_line に一致することの確認:
demo_series1
| extend series_fit_line(y)
| extend series_fit_poly(y)
| project-rename y_line = series_fit_line_y_line_fit, y_poly = series_fit_poly_y_poly_fit
| fork (project x, y, y_line, y_poly) (project-away id, x, y, y_line, y_poly)
| render linechart with(xcolumn=x, ycolumns=y, y_line, y_poly)
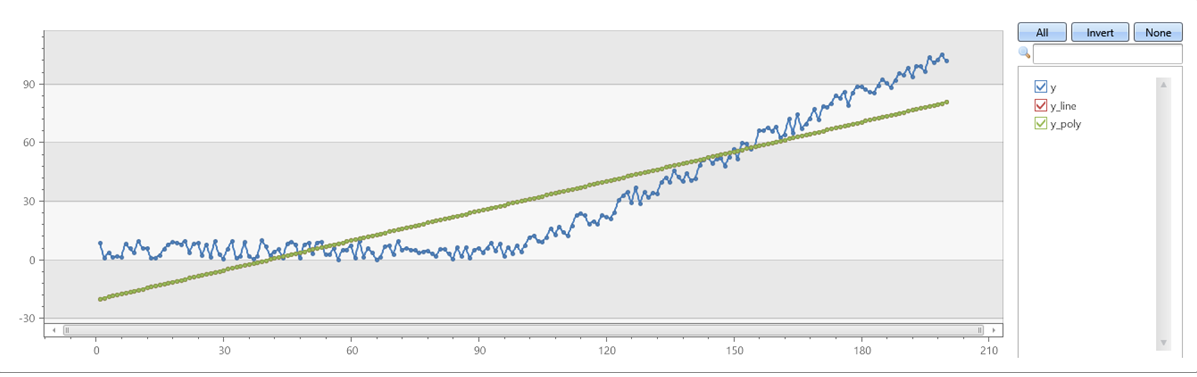

例 3
不規則な (等間隔ではない) 時系列:
//
// x-axis must be normalized to the range [0-1] if either degree is relatively big (>= 5) or original x range is big.
// so if x is a time axis it must be normalized as conversion of timestamp to long generate huge numbers (number of 100 nano-sec ticks from 1/1/1970)
//
// Normalization: x_norm = (x - min(x))/(max(x) - min(x))
//
irregular_ts
| extend series_stats(series_add(TimeStamp, 0)) // extract min/max of time axis as doubles
| extend x = series_divide(series_subtract(TimeStamp, series_stats__min), series_stats__max-series_stats__min) // normalize time axis to [0-1] range
| extend series_fit_poly(num, x, 8)
| project-rename fnum=series_fit_poly_num_poly_fit
| render timechart with(ycolumns=num, fnum)