양자 회로 다이어그램 규칙
회로 다이어그램에서 양자 알고리즘을 동일한 서면 행렬 표현보다 이해하기 쉬운 경우가 있습니다. 이 문서에서는 양자 회로 다이어그램 및 해당 규칙을 읽는 방법을 설명합니다.
자세한 내용은 양자 회로 다이어그램을 시각화하는 방법을 참조 하세요.
양자 회로 다이어그램 읽기
양자 회로에서 시간은 왼쪽에서 오른쪽으로 흐릅니다. 양자 게이트는 게이트가 큐비트에 처음 적용될 때 가장 왼쪽 게이트를 사용하여 시간순으로 정렬됩니다.
다음 양자 회로 다이어그램을 예로 들어 보세요.
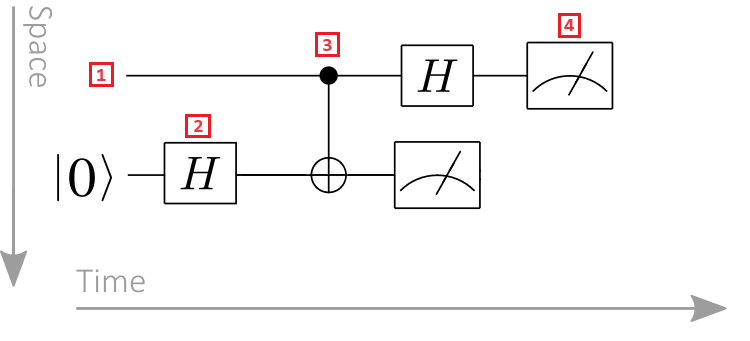
- 큐비트 레지스터: 큐비트 레지스터는 수평선으로 표시되고 각 줄은 큐비트를 나타냅니다. 위쪽 줄은 0으로 레이블이 지정된 큐비트 레지스터이고, 두 번째 줄은 큐비트 레지스터 레이블이 1인 큐비트 레지스터입니다.
- 양자 게이트: 양자 연산은 양자 게이트로 표시됩니다. 양자 게이트라는 용어는 클래식 논리 게이트와 유사합니다. 하나 이상의 큐비트 레지스터에서 작동하는 게이트는 상자로 표시됩니다. 이 예제에서 기호는 Hadamard 작업을 나타냅니다.
- 제어 게이트: 제어 게이트는 둘 이상의 큐비트에서 작동합니다. 이 예제에서 기호는 CNOT 게이트를 나타냅니다. 검은색 원은 컨트롤 큐비트를 나타내고 원 내의 십자가는 target 큐비트를 나타냅니다.
- 측정 작업: 측정기 기호는 측정 작업을 나타냅니다. 측정 작업은 큐비트 레지스터를 입력으로 사용하고 클래식 정보를 출력합니다.
양자 게이트 적용
시간이 왼쪽에서 오른쪽으로 흐르기 때문에 가장 왼쪽 게이트가 먼저 적용됩니다. 예를 들어 다음 양자 회로의 동작은 단위 행렬 $CBA$입니다.
참고 항목
행렬 곱셈은 반대의 규칙을 따릅니다. 가장 오른쪽에 있는 행렬이 먼저 적용됩니다. 그러나 양자 회로 다이어그램에서는 가장 왼쪽에 있는 게이트가 먼저 적용됩니다. 이러한 차이는 때때로 혼동을 야기할 수 있으므로 선형 대수 표기법과 양자 회로 다이어그램 간의 이 중요한 차이점을 유의해야 합니다.
양자 회로의 입력 및 출력
양자 회로 다이어그램에서 양자 게이트로 들어오는 전선은 양자 게이트에 입력되는 큐비트를 나타내고, 양자 게이트를 빠져 나가는 전선은 양자 게이트에서 출력되는 큐비트를 나타냅니다.
양자 게이트의 입력 수는 양자 게이트의 출력 수와 같습니다. 양자 연산은 단위적이므로 되돌릴 수 있기 때문입니다. 양자 게이트에 입력보다 더 많은 출력이 있는 경우 되돌릴 수 없으므로 단위가 아니므로 모순입니다.
이러한 이유로 회로 다이어그램에 그려진 상자는 종료할 때와 정확히 동일한 수의 와이어를 입력해야 합니다.
다중 큐비트 작업
다중 큐비트 회로 다이어그램은 단일 큐비트와 유사한 규칙을 따릅니다. 예를 들어 2큐비트 단위 연산 $B$를 (H S$ X)\otimes로 정의할 $수 있으므로 동등한 양자 회로는 다음과 같습니다.
또한 회로가 사용되는 컨텍스트에 따라 두 개의 1큐비트 레지스터가 아닌 단일 2큐비트 레지스터에 대한 작업이 있는 것으로 B$를 볼 $수 있습니다.
아마도 이러한 추상 회로 다이어그램의 가장 유용한 속성은 기본 게이트 수준까지 컴파일하지 않고도 복잡한 양자 알고리즘을 높은 수준에서 설명할 수 있다는 점일 것입니다. 즉, 알고리즘 내의 각 서브루틴이 작동하는 방식에 대한 모든 세부 정보를 이해할 필요 없이 큰 양자 알고리즘의 데이터 흐름에 대한 직관을 얻을 수 있습니다.
제어 게이트
양자 제어 게이트는 컨트롤 큐비트가 특정 상태에 있는 경우 큐비트에 단일 큐비트 게이트 target 를 적용하는 2큐비트 게이트입니다.
예를 들어, 단일 큐비트의 값이 $G$ 연산의 적용을 제어하는 $\Lambda(G)$로 나타낼 수 있는 양자 제어 게이트를 생각해 보십시오. 제어 게이트 $\Lambda(G)$ 는 제품 상태 입력의 다음 예제를 확인하여 이해할 수 있습니다.
$$\Lambda(G) (\alpha\ket{{0} + \beta\ket{1}) \ket{\psi}=\alpha\ket{{0}\ket{\psi} + \beta\ket{{1} G\ket{\psi}$$
즉, 제어 게이트는 컨트롤 큐비트가 값 $1$을 사용하는 경우에만 포함하는 $\psi$ 레지스터에 G$를 적용$합니다. 일반적으로 이러한 제어된 작업은 회로 다이어그램에서 다음 기호로 설명됩니다.
여기서 검정 원은 게이트가 제어되는 양자 비트를 표시하고 세로 와이어는 컨트롤 큐비트가 값 $1$을 사용할 때 적용되는 단위를 나타냅니다.
G$X= 및 $G$Z=의 특수한 경우 $다음 표기법을 사용하여 제어된 게이트 버전을 설명합니다(제어된 X 게이트는 CNOT 게이트).
Q# 는 제어된 버전의 작업을 자동으로 생성하는 메서드를 제공하여 프로그래머가 이러한 작업을 코딩할 필요가 없도록 합니다. 관련 예시는 아래와 같습니다.
operation PrepareSuperposition(qubit : Qubit) : Unit
is Ctl { // Auto-generate the controlled specialization of the operation
H(qubit);
}
고전적으로 제어되는 게이트
측정 후에 양자 게이트를 적용할 수도 있습니다. 여기서 측정 결과는 클래식 컨트롤 비트로 작동합니다.
다음 기호는 클래식 제어 게이트를 나타내며, 여기서 $G$ 는 값 $1$이 되는 클래식 컨트롤 비트에 조건부로 적용됩니다.
측정 연산자
측정 작업은 큐비트 레지스터를 사용하여 측정하고 결과를 클래식 정보로 출력합니다.
측정 연산은 미터 기호로 표시되고 항상 큐비트 레지스터를 입력(실선으로 표시)으로 취하며, 클래식 정보(이중선으로 표시)를 출력합니다. 특히 측정 작업의 기호는 다음과 같습니다.
에서 Q#연산자는 Measure 측정 작업을 구현합니다.
예: 단위 변환
단위 변환 $\text{CNOT}_{01}(H\otimes 1)$를 고려합니다. 이 게이트 시퀀스는 최대로 얽힌 2큐비트 상태를 만들기 때문에 양자 컴퓨팅에 근본적으로 중요한 사항입니다.
$$\text{CNOT}_{01}(H\otimes 1)\ket{00}=\frac{1}{\sqrt{2}}(\ket{{00} + \ket{11})$$
이러한 복잡성 이상의 작업은 양자 알고리즘 및 양자 오류 수정에서 유비쿼터스입니다.
최대로 얽힌 양자 상태를 준비하기 위한 회로 다이어그램은 다음과 같습니다.
Hadamard 게이트 뒤에 있는 기호는 CNOT 게이트를 나타내며, 검은색 원은 컨트롤 큐비트를 나타내고 원 안의 십자가는 큐비트를 나타냅니다 target . 이 양자 회로는 두 개의 큐비트(또는 하나의 큐비트로 구성된 두 개의 레지스터)에서 작동하는 것으로 표시됩니다.
예: 텔레포트 회로 다이어그램
양자 텔레포트는 회로 구성 요소를 보여 주는 최고의 양자 알고리즘 중 하나입니다.
양자 텔레포트는 한 큐비트에서 다른 큐비트로 양자 상태를 전송할 수 있도록 하는 프로토콜로, 발신자와 수신자 간의 공유 얽힌 상태와 그 간의 클래식 통신을 지원합니다.
학습 목적으로 발신자를 Alice라고 하고, 수신자를 Bob이라고 하며, 텔레포트할 큐비트를 메시지 큐비트라고 합니다. Alice와 Bob은 각각 하나의 큐비트를 보유하며 Alice에는 메시지 큐비트인 추가 큐비트가 있습니다.
다음 회로 다이어그램은 텔레포트 프로토콜을 보여 줍니다.
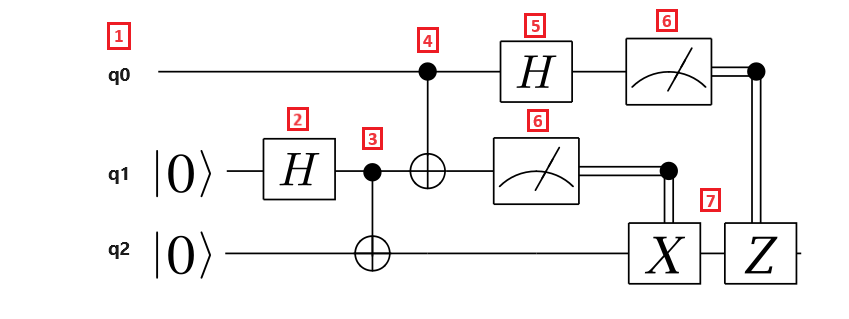
텔레포트 프로토콜의 단계를 세분화해 보겠습니다.
- 큐비트 레지스터 q0 은 메시지 큐비트이고, 큐비트 레지스터 q1 은 Alice의 큐비트이고, 큐비트 레지스터 q2 는 Bob의 큐비트입니다. 메시지 큐비트는 알 수 없는 상태이며 Alice와 Bob의 큐비트는 상태에 있습니다 $\ket{0}$ .
- 하다마드 게이트는 앨리스의 큐비트에 적용됩니다. 큐비트가 $\ket{0}$ 상태에 있으므로 결과 상태는 ($\frac{1}{\sqrt{{2}}+ \ket{){0}입니다\ket{1}$.
- CNOT 게이트는 Alice와 Bob의 큐비트에 적용됩니다. Alice의 큐비트는 컨트롤 큐비트이고 Bob의 큐비트는 큐비트입니다 target . 결과 상태는 ($\frac{+ {1}{\sqrt{2}}\ket{00})\ket{입니다{11}$. 이제 Alice와 Bob은 얽힌 상태를 공유합니다.
- CNOT 게이트는 메시지 큐비트와 Alice의 큐비트에 적용됩니다. Alice의 큐비트도 Bob의 큐비트와 얽혀 있으므로 결과 상태는 3큐비트 얽힌 상태입니다.
- 메시지 큐비트에 Hadamard 게이트가 적용됩니다.
- Alice 는 두 개의 큐비트를 측정 하고 측정 결과를 Bob에게 알려주며, 이는 회로에 반영되지 않습니다. 측정 결과는 00, 01, 10 또는 11 값을 사용할 수 있는 두 개의 클래식 비트입니다.
- 두 개의 고전적으로 제어된 Pauli 게이트 X와 Z는 값 1$인 결과 비트에 따라 Bob의 큐비트에$됩니다. 결과 상태는 원래 메시지 큐비트 상태입니다.