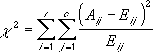WorksheetFunction.ChiTest method (Excel)
Returns the test for independence.
Important
This function has been replaced with one or more new functions that may provide improved accuracy and whose names better reflect their usage. This function is still available for compatibility with earlier versions of Excel. However, if backward compatibility is not required, you should consider using the new functions from now on, because they more accurately describe their functionality.
For more information about the new function, see the ChiSq_Test method.
Syntax
expression.ChiTest (Arg1, Arg2)
expression A variable that represents a WorksheetFunction object.
Parameters
| Name | Required/Optional | Data type | Description |
|---|---|---|---|
| Arg1 | Required | Variant | The range of data that contains observations to test against expected values. |
| Arg2 | Required | Variant | The range of data that contains the ratio of the product of row totals and column totals to the grand total. |
Return value
Double
Remarks
ChiTest returns the value from the chi-squared (χ2) distribution for the statistic and the appropriate degrees of freedom. Use χ2 tests to determine whether hypothesized results are verified by an experiment.
If actual_range and expected_range have a different number of data points, ChiTest returns the #N/A error value.
The χ2 test first calculates an χ2 statistic by using the following formula, where:
- Aij = actual frequency in the i-th row, j-th column
- Eij = expected frequency in the i-th row, j-th column
- r = number or rows
- c = number of columns
A low value of χ2 is an indicator of independence. As can be seen from the formula, χ2 is always positive or 0, and is 0 only if Aij = Eij for every i,j.
ChiTest returns the probability that a value of the χ2 statistic at least as high as the value calculated by the preceding formula could have happened by chance under the assumption of independence. In computing this probability, ChiTest uses the χ2 distribution with an appropriate number of degrees of freedom, df.
- If r > 1 and c > 1, then df = (r - 1)(c - 1).
- If r = 1 and c > 1, then df = c - 1.
- If r > 1 and c = 1, then df = r - 1.
- r = c = 1 is not allowed and generates an error.
Use of ChiTest is most appropriate when Eij's are not too small. Some statisticians suggest that each Eij should be greater than or equal to 5.
Support and feedback
Have questions or feedback about Office VBA or this documentation? Please see Office VBA support and feedback for guidance about the ways you can receive support and provide feedback.