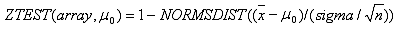WorksheetFunction.ZTest method (Excel)
Returns the one-tailed probability-value of a z-test. For a given hypothesized population mean, ZTest returns the probability that the sample mean would be greater than the average of observations in the data set (array); that is, the observed sample mean.
Important
This function has been replaced with one or more new functions that may provide improved accuracy and whose names better reflect their usage. This function is still available for compatibility with earlier versions of Excel. However, if backward compatibility is not required, you should consider using the new functions from now on, because they more accurately describe their functionality.
For more information about the new function, see the Z_Test method.
Syntax
expression.ZTest (Arg1, Arg2, Arg3)
expression A variable that represents a WorksheetFunction object.
Parameters
| Name | Required/Optional | Data type | Description |
|---|---|---|---|
| Arg1 | Required | Variant | Array is the array or range of data against which to test the hypothesized population mean. |
| Arg2 | Required | Double | The value to test. |
| Arg3 | Optional | Variant | Sigma is the population (known) standard deviation. If omitted, the sample standard deviation is used. |
Return value
Double
Remarks
If array is empty, ZTest returns the #N/A error value.
ZTest is calculated as follows when sigma is not omitted:
ZTest is calculated as follows when sigma is omitted, where x is the sample mean AVERAGE(array), s is the sample standard deviation STDEV(array), and n is the number of observations in the sample COUNT(array):
ZTest represents the probability that the sample mean would be greater than the observed value AVERAGE(array), when the underlying population mean is μ0. From the symmetry of the Normal distribution, if AVERAGE(array) < μ0, ZTest will return a value greater than 0.5.
The following Excel formula can be used to calculate the two-tailed probability that the sample mean would be further from μ0 (in either direction) than AVERAGE(array), when the underlying population mean is μ0:
=2 * MIN(ZTEST(_array_,μ0,_sigma_), 1 - ZTEST(_array_,μ0,_sigma_)).
Support and feedback
Have questions or feedback about Office VBA or this documentation? Please see Office VBA support and feedback for guidance about the ways you can receive support and provide feedback.