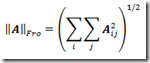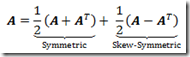The “Cloud Numerics” Programming and runtime execution model
Microsoft Codename “Cloud Numerics” is a new .NET® programming framework tailored towards performing numerically-intensive computations on large distributed data sets. It consists of
- a programming model that exposes the notion of a partitioned or distributed array to the user
- an execution framework or runtime that efficiently maps operations on distributed arrays to a collection of nodes in a cluster
- an extensive library of pre-existing operations on distributed arrays and tools that simplify the deployment and execution of a “Cloud Numerics” application on the Windows Azure™ platform
Programming frameworks such as Map/Reduce [2, 3] (and its open-source counterpart, Hadoop [6]) have evolved to greatly simplify the processing of large datasets. These frameworks expose a very simple end-user programming model and the underlying execution engine abstracts away most of the details of running applications in a highly scalable manner on large commodity clusters. These simplified models are adequate for performing relational operations and implementing clustering and machine learning algorithms on data that is too large to fit into the main memory of all the nodes in a cluster. However, they are often not optimal for cases when the data does fit into the main memory of the cluster nodes. Additionally, algorithms that are inherently iterative in nature or that are most conveniently expressed in terms of computations on arrays are difficult to express using these simplified programming models. Finally, while the Hadoop ecosystem is extremely vibrant and has developed multiple libraries such as Mahout [6], Pegasus [5] and HAMA for data analysis and machine learning, these currently do not leverage existing, mature scalable linear algebra libraries such as PBLAS and ScaLAPACK that have been developed and refined over several years.
In contrast, libraries such as the Message Passing Interface or MPI [6] are ideally suited for efficiently processing in-memory data on large clusters, but are incredibly difficult to program correctly and efficiently. A user of the library has to carefully orchestrate the movement of data between the various parallel processes. Unless this is done with a lot of care, the resulting “high performance” application will exhibit extremely poor scalability or worse, crash or hang in a non-deterministic manner.
The programming abstractions provided by “Cloud Numerics” do not expose any low-level parallel-processing constructs. Instead, parallelism is implicit and automatically derived from operations on data types that are provided by the framework such as distributed matrices. These parallel operations in turn map to efficient implementations that in turn utilize existing high-performance libraries such as the PBLAS and ScaLAPACK libraries mentioned above.
The rest of this document provides an overview of the programming and runtime execution models in “Cloud Numerics” and is intended to complement the quick start guide and the library API reference.
A “Hello World” example in “Cloud Numerics”
To briefly illustrate the parallel programming model in “Cloud Numerics”, the following C# sample code first loads a distributed matrix, computes its singular values in parallel and prints out its two-norm and condition number with respect to the two-norm:
var A = Distributed.IO.Loader.LoadData<double>(csvReader);
var S = Decompositions.SvdValues(A);
var s0 = ArrayMath.Max(S);
var s1 = ArrayMath.Min(S);
Console.WriteLine("Norm: {0}, Condition Number: {1}", s0, s0 / s1);
What “Cloud Numerics” is not
While the rest of this document provides more details on the programming and execution model in “Cloud Numerics”, it is important to briefly emphasize what it is not.
First, the “Cloud Numerics” programming model is primarily based around distributed array operations (c.f. data parallel or SIMD-style of programming). Certain relational operations such as “selects” with user-defined functions or complex joins are simpler to express on top of languages such as Pig, Hive and SCOPE. Similarly, while “Cloud Numerics” is designed to deal with large data sets, it is currently constrained to operate on arrays that can fit in the main memory of a cluster. On the other hand, data on disk can be pre-processed via existing “big data” processing tools and ingested into a “Cloud Numerics” application for further processing.
Second, “Cloud Numerics” is not just a convenient C# wrapper around message-passing libraries such as MPI, for example MPI.NET [3]; all aspects of parallelism are expressed via operations on distributed arrays and the “Cloud Numerics” runtime transparently handles the efficient execution of these high-level array operations on a cluster.
A key aspect that distinguishes “Cloud Numerics” from parallelization techniques such as PLINQ and DryadLINQ [4], that are based on implementing a custom LINQ provider, is that parallelization in “Cloud Numerics” occurs purely at runtime and does not involve any code generation from (say) LINQ expression trees; a user’s application can be developed as a regular .NET application by referencing the “Cloud Numerics” runtime and library DLLs and executed on the cluster in Azure.
Finally, the underlying communication layer in “Cloud Numerics” is built on top of the message passing interface (MPI) and does inherit some of the limitations in the underlying implementation such as:
- The process model is currently inelastic; once a “Cloud Numerics” application has been launched on (say) P cores in a cluster, it is not possible to dynamically grow or shrink the resources as the application is running.
- The implementation is not resilient against hardware failure. Unlike frameworks like Hadoop that are designed explicitly to operate on unreliable hardware, if one or more nodes in a cluster fails, it is not possible for a “Cloud Numerics” application to automatically recover and continue executing.
On the other hand, having MPI as the underlying communication layer in the “Cloud Numerics” runtime does endow it with certain advantages. For instance, “Cloud Numerics” applications can automatically take advantage of high-speed interconnects such as Infiniband between nodes in a cluster and optimizations such as zero-copy memory transfers and shared-memory-aware collectives within a single multi-core node. More importantly, array operators in “Cloud Numerics” can leverage the vast ecosystem of high-performance distributed memory numerical libraries such as ScaLAPACK built on top of MPI.
What this document does and does not cover
The intent of this document is to provide an overview of the programming model in “Cloud Numerics” along with a high-level description of how a “Cloud Numerics” application runs in parallel on a cluster of machines. It does not for example cover the extensive library of numerical functions in “Cloud Numerics” for operating on local and distributed arrays, the programming interfaces provided to import and export data in parallel and the details of how a “Cloud Numerics” application is deployed on a cluster on Windows Azure from the client and executed.
High-level overview
Figure 1 illustrates the main components in a distributed “Cloud Numerics” application. The end-user or client application is itself written in a CLI (Common Language Infrastructure) language such as C#, VisualBasic.NET or F# against a set of .NET APIs provided by the “Cloud Numerics” libraries. These interfaces primarily consist of a set of local and distributed high-performance array data types along with a large collection of array operations; there are no additional interfaces for parallel programming such as task creation and synchronization, resource management, etc. Once an application is running on a cluster of machines, the runtime automatically partitions the data between the nodes in the cluster and executes operations on partitioned data in parallel.
Operations on distributed or partitioned arrays in turn depend upon a set of runtime services for handling distributed function execution, error handling and input/output operations. In addition, the “Cloud Numerics” system provides a set of tools to simplify development, deployment and execution of a distributed application on Azure from a local client machine.
Under the covers, the programming interfaces are implemented as thin wrappers around a native runtime and library infrastructure. These consist of lower-level local and distributed array objects along with interfaces for performing operations on them. Several operations on distributed arrays leverage existing high-performance numerical libraries such as BLAS and LAPACK on a single CPU core and PBLAS, BLACS and ScaLAPACK across CPU cores. At the lowest level are inter-process communication libraries such as MPI and C and C++ runtime libraries for memory management and exception handling.
Figure 1. The components in a “Cloud Numerics” application.
The “Cloud Numerics” Programming Model
As mentioned previously, “Cloud Numerics” is ideally suited for algorithms that can be expressed in terms of high-level operations on multi-dimensional arrays.
For instance, consider the “power iteration” algorithm for computing the largest eigenvector of a matrix. Power iteration is at the heart of several fundamental graph-theoretic computations such as the PageRank for a collection of web pages. If the collection of pages is represented as a matrix A where Aij is non-zero when page i is connected to page j, the principal eigenvector can be computed roughly as follows:
Arrays such as the web-connectivity matrix described above are fundamental types in “Cloud Numerics”. Further, vector operations such as x(0) = x(0) / |x(0| and array operations such as x(1) = Ax(0) can be expressed succinctly using the “Cloud Numerics” library and executed efficiently even when the vectors and matrices are very large and are therefore partitioned between several nodes in a cluster.
On the flip side, the “Cloud Numerics” programming model may not be a good fit for algorithms that cannot be easily expressed in array notation (such as relational joins between two data sets) or for applications such as parsing and simplifying petabytes of text data where numerical computation is not the main bottleneck. However, once the data has been “boiled-down” and transformed to its core numerical structure, it can be further analyzed using “Cloud Numerics”.
Arrays in “Cloud Numerics”
All array types in “Cloud Numerics”, be they dense or sparse, local or distributed implement the Microsoft.Numerics.IArray<T> interface, where the generic parameter T refers to the type of elements in the array. The IArray interface provides fundamental properties such as Shape, NumberOfDimensions and NumberOfElements, indexers and basic methods such as Transpose, Reshape and Flatten that are supported by all array sub-types. Note that arrays in “Cloud Numerics” are always multi-dimensional (i.e., there is no notion of distinct Matrix or Vector types).
Array element types
Both local and distributed arrays support the following element types: boolean, one-byte, two-byte, four-byte and eight-byte signed and unsigned integers, single and double-precision real floating point numbers and single and double-precision complex floating point numbers. The corresponding .NET types are listed below:
Array element type |
Description |
Range of values |
System.Boolean |
Single-byte logical values |
true/false |
System.UInt8 |
Single-byte unsigned integers |
[0,255] |
System.Int8 |
Singled-byte signed integers |
[-128,127] |
System.UInt16 |
Two-byte unsigned integers |
[0,216-1] |
System.Int16 |
Two-byte signed integers |
[-215,215-1] |
System.UInt32 |
Four-byte unsigned integers |
[0,232-1] |
System.Int32 |
Four-byte signed integers |
[-231,231-1] |
System.UInt64 |
Eight-byte unsigned integers |
[0,264-1] |
System.Int64 |
Eight-byte signed integers |
[-263,263-1] |
System.Single |
Single-precision IEEE 754 real floating point values |
[-infinity, infinity] |
System.Double |
Double-precision IEEE 754 real floating point values |
[-infinity, infinity] |
Microsoft.Numerics.Complex64 |
Single-precision complex values |
|
Microsoft.Numerics.Complex128 |
Double-precision complex values |
Indexing and iteration
An important interface that IArray<T> in turn implements is the .NET enumerable interface IEnumerable<T>. Therefore, methods in .NET, for instance LINQ operators that accept IEnumerable<T> can be passed instances of “Cloud Numerics” arrays.
Array broadcasting
In NumPy [2], broadcasting refers to two related concepts: (a) the application of a scalar function to every element of an array producing an array of the same shape and (b) the set of rules governing how two or more input arrays of different shapes are combined under an element-wise operation. In environments such as NumPy and “Cloud Numerics” that support a rich set of operations on multi-dimensional arrays, broadcasting is often used as a convenient mechanism for implementing certain forms of iteration.
Several element-wise operators and functions in “Cloud Numerics” support broadcasting using conventions similar to NumPy. For example, given a local or distributed array A and a scalar s, Microsoft.Numerics.BasicMath.Sin(A) applies the sin function and A + s adds s to each element of A. Similarly, for a vector v containing the same number of rows of A, A – v subtracts v from every column of A (in other words, “Cloud Numerics” broadcasts the vector v along the columns of A) [Note: In the first version “Cloud Numerics” only supports broadcasting for scalars, but this deficiency will be addressed for the next release.]
Local arrays in “Cloud Numerics”
Before describing the programming model for distributed arrays, it is instructive to first understand the model for interacting with local arrays in “Cloud Numerics” since distributed arrays support practically the same semantics as local arrays except with different performance characteristics.
The most important local array type in “Cloud Numerics” is Microsoft.Numerics.Local.NumericDenseArray<T> which represents a dense multi-dimensional array with numerical values. As mentioned previously, dense arrays can have an arbitrary number of dimensions (so it is possible to create and operate on say, a 10-dimensional array just as easily as a two- or three-dimensional array)
Underlying storage
Dense local arrays in “Cloud Numerics” are not backed by arrays allocated in the .NET/CLR heap. This is primarily because arrays allocated in the CLR are currently constrained to be smaller than two Gigabytes whereas the ones allocated on the native heap do not have this limitation. Additionally, the underlying native array types in the “Cloud Numerics” runtime are sufficiently flexible that they can be easily wrapped in environments other than .NET (say Python or R) with very little additional effort.
Unlike arrays in .NET that are internally stored in row-major order, multi-dimensional arrays in “Cloud Numerics” are represented in column-major order that allows for efficient interoperability with high-performance numerical libraries such as BLAS and LAPACK.
Array factory type
The local NumericDenseArray class does not provide any public constructors; users are expected to create instances of local arrays using a factory class, NumericDenseArrayFactory that provides a number of static array creation methods. For example, to create a local 4 x 10 x 12 array of double-precision values filled with zero, one would use:
var doubleArray = NumericDenseArrayFactory.Zeros<double>(4, 10, 12);
Interoperability with .NET arrays
As mentioned above, arrays in “Cloud Numerics” are not backed by .NET arrays; instead, the NumericDenseArrayFactory provides a method to create a new “Cloud Numerics” array from a .NET array. For example, to create a new local array from a 2 x 2 .NET array, one would use:
var aDotNetArray = new double[,]{{1.0, 2.0}, {3.0, 4.0}};
var cnArray = NumericDenseArrayFactory.CreateFromSystemArray<double>(aDotNetArray);
Conversely, the NumericDenseArray class provides two methods that return .NET arrays: one for returning a multi-dimensional .NET array of the same shape and with the same elements as the NumericDenseArray instance and other for returning a one-dimensional .NET array that contains the elements flattened in row-major order. These are shown in the code snippets below:
double[,] anotherDotNetArray = (double[,]) cnArray.ToSystemArray();
double[] flatDotNetArray = cnArray.ToFlatSystemArray();
Indexing and iteration with local arrays
A local array in “Cloud Numerics” can be indexed by a scalar just like any other multi-dimensional array in .NET. Currently, indices are constrained to be scalars and the number of indices must be the same as the number of dimensions of the array as shown in the following examples:
double twoDValue = twoDArray[3, 4];
double threeDValue = threeDArray[2, 3, 4];
Similarly, local arrays support iteration over the elements in flattened column-major order. For instance, one could compute the Frobenius norm of a matrix A defined as:
using the following LINQ expression:
var froNorm = Math.Sqrt(doubleMatrix.Select((value) => value * value).Sum());
Other operations
In addition to the primitive operations shown in this section, local arrays in “Cloud Numerics” also support operations such as element-wise arithmetic and logical operators, reshaping an existing array to a different shape while preserving the order of elements in memory, transposing an array and filling the elements of an array using a generator function. For example, given a general matrix A, one could decompose it into a sum of a symmetric and a skew-symmetric matrix:
using:
var sym = 0.5 * (matrix + matrix.Transpose());
var skewSym = 0.5 * (matrix - matrix.Transpose());
Distributed Arrays
In “Cloud Numerics”, the end-user creates and interacts with a single instance of a distributed array. However, under the covers, the runtime creates several arrays on a number of locales and partitions the global distributed array between them [Note: A locale is defined in the section on the execution model, but it can be thought of as a process containing a portion of a distributed array.] Every aggregate operation on a global distributed array (say computing the sum of its columns or permuting its elements) is transparently transformed by the “Cloud Numerics” runtime into one or more parallel operations on these array partitions.
Partitioning of arrays
This section briefly summarizes the partitioning scheme for distributed arrays in “Cloud Numerics”. Note however that the “Cloud Numerics” runtime automatically handles the partitioning of arrays between several locales and the user normally does not need to specify any aspects of data distribution.
A distributed array is constrained to be partitioned across the locales only along one of its dimensions. The dimension along with an array is partitioned is referred to as its distributed dimension. Each locale then gets a contiguous set of slices of the partitioned array along the distributed dimension; the set of indices along the distributed dimension corresponding to the slices assigned to a particular locale constitute the span of the array on that locale. Finally, each locale always gets complete slices of the distributed array and the slices between two different locales never overlap.
The partitioning scheme described above is illustrated in Figure 2 for a matrix that is distributed across three locales, first by rows and second by columns.
By default, a multidimensional array is always distributed along its last non-singleton dimension. For instance, a 1000 x 1000 matrix is distributed by columns whereas a 1000 x 1 vector is distributed by rows.
Figure 2. Row and column partitioned arrays.
Propagation of distributions
Generally, methods and static functions in “Cloud Numerics” that return arrays produce distributed outputs given distributed inputs (the ToLocalArray method and functions that return scalars such as SUM are important exceptions to this rule). The precise manner in which the distribution propagates is as follows: if one or more input arguments to a function are arrays, the distributed dimension of the output is the maximum of the distributed dimension of all the inputs. If this distributed dimension is greater than the last non-singleton dimension of the output, the output is distributed along its last non-singleton dimension.
Distributed array types
All distributed arrays in “Cloud Numerics” implement the Microsoft.Numerics.Distributed.IArray<T> interface where T is the type of elements in the distributed array. Besides the properties and methods that the base Microsoft.Numerics.IArray<T> interface provides, the distributed array interface provides two important properties: DistributedDimension and Span as well as a Redistribute method that redistributes the array along a different dimension.
Working with distributed arrays
The fundamental distributed array type in “Cloud Numerics” is Microsoft.Numerics.Distributed.NumericDenseArray<T>. Unlike their local counterparts, distributed arrays provide explicit constructors. For example to create a new distributed double-precision dense array of shape 100 x 100 x 5000 one would use:
var dArray = new Distributed.NumericDenseArray<double>(100, 100, 500);
Conversion between local and distributed arrays
Local arrays are implicitly converted to distributed arrays by assignment. As a consequence any function that only takes a distributed array as an input can be passed a local array and the runtime will transparently “promote” the local array to be distributed.
var lArray = Local.NumericDenseArrayFactory.Create<double>(400, 400);
Distributed.NumericDenseArray<double> dArray = lArray;
On the other hand, a distributed array cannot be implicitly converted to a local array since they are assumed to be much larger than what can fit into the memory of a local machine. Therefore, converting a distributed array to a local array requires the user to explicitly call the NumericDenseArray<T>.ToLocalArray() method. In a similar fashion, a distributed array can be converted to a .NET array via the NumericDenseArray<T>.ToSystemArray method.
var dArray = new Distributed.NumericDenseArray<double>(100, 100, 500);
var lArray = dArray.ToLocalArray();
var csArray = dArray.ToSystemArray();
Indexing distributed arrays
Distributed arrays can be indexed by scalars just like their local counterparts. For example, the following snippet shows indexing into two- and three-dimensional arrays:
double twoDValue = twoDDistArray[3, 4];
double threeDValue = threeDDistArray[2, 3, 4];
Unlike local arrays, distributed arrays do not support iterating over the elements. This is primarily because there is no built-in facility in .NET for iterating over partitioned collections in parallel. [Note: This could potentially be done by implementing a custom LINQ provider.]
Other distributed array operations
Distributed arrays support almost exactly the same set of operations that are supported by local arrays. For instance, the earlier example of decomposing an array into a symmetric and skew-symmetric matrix:
var sym = 0.5 * (matrix + matrix.Transpose());
var skewSym = 0.5 * (matrix - matrix.Transpose());
works unmodified when the argument is a distributed matrix.
Expressing parallelism in “Cloud Numerics”
As mentioned several times in this document, the primary mechanism in “Cloud Numerics” for expressing parallelism is via aggregate (data-parallel) operations on distributed arrays; “Cloud Numerics” currently does not support other modes of parallelism such as task or control parallelism.
As an example, the following code segment illustrates an alternate implementation of decomposing a matrix into its symmetric and skew-symmetric components:
var dims = matrix.Shape.ToArray();
var sym = new Distributed.NumericDenseArray<double>(dims);
var skewSym = new Distributed.NumericDenseArray<double>(dims);
for (long j = 0; j < dims[1]; j++)
{
for (long i = 0; i < dims[0]; i++)
{
sym[i, j] = 0.5 * (matrix[i, j] + matrix[j, i]);
sym[i, j] = 0.5 * (matrix[i, j] - matrix[j, i]);
}
}
While this code is syntactically correct and will produce the correct answer for a distributed array, it will not execute in parallel due to its use of the C# (sequential) loop construct. Further, the scalar indexing operations (matrix[i, j], sym[i, j] and sym[i, j]) are highly sub-optimal for distributed arrays since each scalar access generates O(logP) communication steps where P is the number of locales. The approach based on array operators such as 0.5 * (matrix + matrix.Transpose()) besides being more concise is also more efficient, possibly by several orders of magnitude.
It is therefore always advantageous in “Cloud Numerics” applications to try and translate fine-grained array accesses into coarse-grained aggregate array operations using mechanisms such as slicing and broadcasting.
The “Cloud Numerics” Runtime Execution Model
Having described the programming model in “Cloud Numerics” based around operations on local and distributed arrays, this section briefly explains how a “Cloud Numerics” application is developed and executed on a cluster. The intent of this section is to once again only provide a high-level overview of the execution model; the “Cloud Numerics” Quick Start Guide provides a detailed walkthrough of developing an application and deploying on to a cluster in Azure.
Application development, debugging and deployment
A “Cloud Numerics” application is initially developed and debugged on a single workstation using the “Cloud Numerics” .NET API. The user can then choose to run the application locally on the workstation either in sequential or parallel modes. When an application is run in the sequential mode, it behaves as any other .NET application and for instance, can be debugged and profiled inside the Visual Studio® IDE.
Once an application is developed and debugged on a single workstation, it can be deployed and executed on a Windows HPC (High-Performance Computing) cluster on Windows Azure using the “Cloud Numerics” deployment wizard.
Process model
Figure 3 illustrates the process model in a “Cloud Numerics” application when executed on a cluster on Azure. Briefly, when a “Cloud Numerics” application is, it starts up a given number, say P copies of the “Cloud Numerics” runtime. These runtime instances are referred to as locales. In Figure 3, each locale is shown on a different physical node, but in reality, the mapping of locales to actual hardware is somewhat arbitrary. For example, on a multi-core node or virtual machine, there can be as many locales as cores in the node. Normally, a user only specifies the number of nodes on which the application must be executed; the HPC Scheduler takes of allocating as many physical cores as required.
The notion of a locale in “Cloud Numerics” is intimately tied to the notion of an operating system process; each locale in fact runs on a separate operating system process even within a single physical node. For this reason, the terms locale and process are interchangeably in the rest of this document.
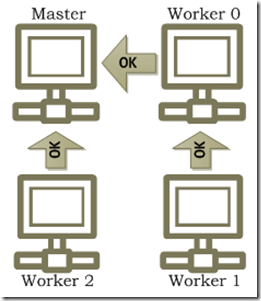
Of the P locales created, one is designated to be the master and the other P- 1 are designated to be worker locales. The user’s application only runs on the master process (in other words, a parallel application in “Cloud Numerics” has a single thread of control) and the remaining P- 1 processes wait in an infinite loop for notification from the master to do work on their portions of a distributed array. A single thread of control from the users’ perspective is an important aspect that makes parallel programming convenient in “Cloud Numerics”; the user does not have to explicitly write or manage the execution of any parallel constructs (such as launching tasks or passing messages between instances) and therefore it is not possible to programmatically run into pitfalls such as starvation or deadlock that are present in other parallel programming models.
Figure 3. A distributed “Cloud Numerics” application executing on a master and three worker processes. The P- 1 processes are interconnected in a topology referred to as a hypercube.
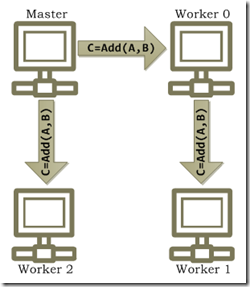
Figures 4 through 6 illustrate the steps involved in performing a distributed operation such as computing the element-wise sum of two partitioned arrays A and B.
First, the user’s application dispatches the operation to the master process via the overloaded addition operator.
Figure 4. First step: the user invokes a method on a distributed array on the master process.
Then, the master process broadcasts the operation to all workers. The payload consists of both the operation to be performed as well as references to the distributed input arguments.
Figure 5. Second step: The command is broadcast from the master to all workers.
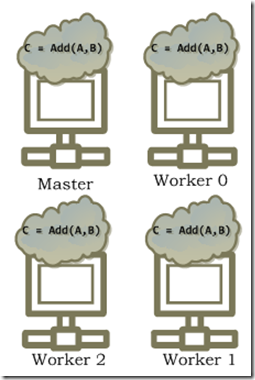
Next, the master and workers perform a part of the underlying computation in parallel. Often, but not always this involves communicating with other locales to exchange data. For example, in the case of element-wise addition, if the two arguments are partitioned such that each locale has all the data necessary to compute its portion of the output, the operation is done element-wise without any communication. On the other hand if say the first argument is partitioned by rows and the second is partitioned by columns, the master and workers first collectively exchange pieces of the first matrix in order to compute the result.
Figure 6. The master and workers work on a part of the computation in parallel. In is particular example, the computation can be performed without requiring any communication.
Once each worker is finished with its portion of the computation, it sends back a successful completion flag to the master. On the other hand, if it fails (say because of an exception), it sends back a specific failure code along with a serialized exception object describing the failure.
Figure 7. Once the master and workers are done with the computation, the master collects any errors during computation. In this particular case, all work is completed successfully.
The master process waits for an acknowledgement from each of the workers. If all processes (including it) completed successfully, the master returns a reference to the result back to the user’s application. On the other hand if one or more workers encountered an error, the master process rethrows the exception in the payload into the application where it can be handled like any other exception in .NET.
Figure 8. The master then returns the result of the computation to the user as a distributed result.
Conclusions
The programming model in “Cloud Numerics”, based around operations on distributed arrays, simplifies the implementation of algorithms that are most naturally expressed in matrix notation and introduces no additional parallel programming or synchronization constructs. Further, the model, based on a single-thread of execution, greatly simplifies application development and debugging and reduces the possibility of conditions such as races and deadlocks due to bugs in the user’s application. The “Cloud Numerics” distributed runtime transparently executes operations on distributed arrays in parallel on nodes in a cluster, leveraging existing mature high-performance libraries when possible.
Although the general principles behind the design and implementation of “Cloud Numerics” are based on well-established fundamentals in high-performance scientific computing, it is still a new and rapidly-evolving framework. It is anticipated that future versions of “Cloud Numerics” will support:
- interoperability with Map/Reduce execution frameworks
- a richer set of functionality on distributed arrays
- operations on distributed sparse matrices
- better performance on existing functions
- more user-friendly application deployment wizard
and most importantly, additional features based on end-user feedback.
References
- Blackford, L.S, Choi, J., Cleary, A., et al. “ScaLAPACK Users’ Guide”, SIAM, Philadelphia, PA, 1997.
- Dean, J. and Ghemawat, S., “MapReduce: Simplified data processing on large clusters”, Symposium on Operating System Design and Implementation (OSDI), 2004.
- Gregor, D. and Lumsdaine, A. “Design and implementation of a high-performance MPI for C# and the Common Language Infrastructure”, ACM Principles and Practice of Parallel Programming, pages 133-142, February 2008.
- Lin, J. and Dyer, C., “Data-intensive Text Processing with MapReduce”, Morgan-Claypool, 2010.
- Kang, U., Tsourakakis, C. E. and Faloutsos, C. “PEGASUS: A Peta-Scale Graph Mining System - Implementation and Observations”, IEEE Conference on Data Mining, 2009.
- Oliphant, T., “A Guide to NumPy”, Trelgol Publishing, 2005.
- Owen, S., Anil, R. and Dunning, T. “Mahout in Action”, Manning Press, 2011.
- Snir, M. and Gropp, W., “MPI – The complete reference”, MIT Press, Cambridge, MA, 1998.
- White, T., “Hadoop: The Definitive Guide, 2e”, O’Reilly, Sebastopol, CA, 2008.
- Yu, Y., Isard M., Fetterly, D., et al. “DryadLINQ: A System for General-Purpose Distributed Data-Parallel Computing Using a High-Level Language”. Symposium on Operating System Design and Implementation (OSDI), San Diego, CA, 2008.
Comments
- Anonymous
February 14, 2012
Hello Ronnie, thanks! great overview for a complex topic! I wonder, if you could point me to some more detailed infos about the memory management inside Cloud Numerics? I am especially concerned about the disposal of used storage in conjunction with the nice array operator syntax shown here? Thanks in advance!