Analisar classificação com curvas de características de operação do receptor
Os modelos de classificação precisam atribuir um exemplo a uma categoria. Por exemplo, ele precisa usar características como tamanho, cor e movimento para determinar se um objeto é um caminhante ou uma árvore.
É possível aprimorar modelos de classificação de várias maneiras. Por exemplo, podemos garantir que os dados sejam balanceados, limpos e escalados. Também é possível alterar a arquitetura de modelo e usar hiperparâmetros para maximizar o desempenho dos dados e da arquitetura. Em última análise, não encontramos uma forma melhor de aprimorar o desempenho no conjunto de teste (ou controle) e declarar nosso modelo como pronto.
Esse tipo de ajuste de modelo pode ser complexo, mas há uma etapa final simples a ser seguida para aprimorar ainda mais o funcionamento do modelo. No entanto, para entender isso, precisamos voltar ao básico.
Probabilidades e categorias
Muitos modelos têm vários estágios de tomada de decisão, e o final geralmente é apenas uma etapa de binarização. Durante a binarização, as probabilidades são convertidas em um rótulo rígido. Por exemplo, imagine que o modelo foi fornecido com características e calcula que há uma probabilidade de 75% de que ele tenha visto um caminhante e uma probabilidade de 25% de que tenha sido uma árvore. Um objeto não pode ser 75% caminhante e 25% árvore: ele é um ou outro. Assim, o modelo aplica um limite, que normalmente é de 50%. Como a classe de caminhante é maior que 50%, o objeto é declarado como um caminhante.
O limite de 50% é lógico: significa que o rótulo mais provável de acordo com o modelo é sempre escolhido. No entanto, se o modelo for parcial, esse limite de 50% poderá não ser apropriado. Por exemplo, se o modelo tiver uma pequena tendência a escolher árvores mais do que caminhantes (escolhendo árvores 10% mais frequentemente do que deveria), será possível ajustar o limite de decisão para considerar isso.
Recapitulação sobre as matrizes de decisão
As matrizes de decisão são uma ótima forma de avaliar os tipos de erros que um modelo comete. Isso nos dá as taxas de TP (verdadeiros positivos), TN (verdadeiros negativos), FP (falsos positivos) e FN (falsos negativos)

Podemos calcular algumas características úteis com base na matriz de confusão. Duas características populares são:
- Taxa de verdadeiros positivos (sensibilidade): com que frequência os rótulos "True" são identificados corretamente como "True". Por exemplo, a frequência com que o modelo prevê "caminhante" quando o exemplo mostrado é, na verdade, um caminhante.
- Taxa de falsos positivos (taxa de alarme falso): com que frequência os rótulos "False" são identificados incorretamente como "True". Por exemplo, com que frequência o modelo prevê "caminhante" quando uma árvore é mostrada.
Observar as taxas de verdadeiros positivos e falsos positivos pode ajudar a compreender o desempenho de um modelo.
Considere o exemplo do caminhante. O ideal é que a taxa de verdadeiros positivos seja muito alta e a de falsos positivos seja muito baixa, porque isso significa que o modelo identifica os caminhantes bem e não identifica árvores como caminhantes com muita frequência. Ainda assim, se a taxa de verdadeiros positivos for muito alta, mas a taxa de falsos positivos também for, o modelo será parcial: ele identificará quase tudo o que encontrar como caminhante. Da mesma forma, você não quer um modelo com uma baixa taxa de verdadeiros positivos, porque quando ele encontrar um caminhante, ele o rotulará como uma árvore.
Curvas ROC
As curvas ROC (características de operação do receptor) são um grafo em que plotamos a taxa de verdadeiros positivos versus a taxa de falsos positivos.
Elas podem ser confusas para iniciantes por dois motivos principais. O primeiro motivo é que os iniciantes sabem que um modelo tem apenas um valor para as taxas de verdadeiros positivos e verdadeiros negativos, portanto, um gráfico ROC pode ser semelhante ao seguinte:
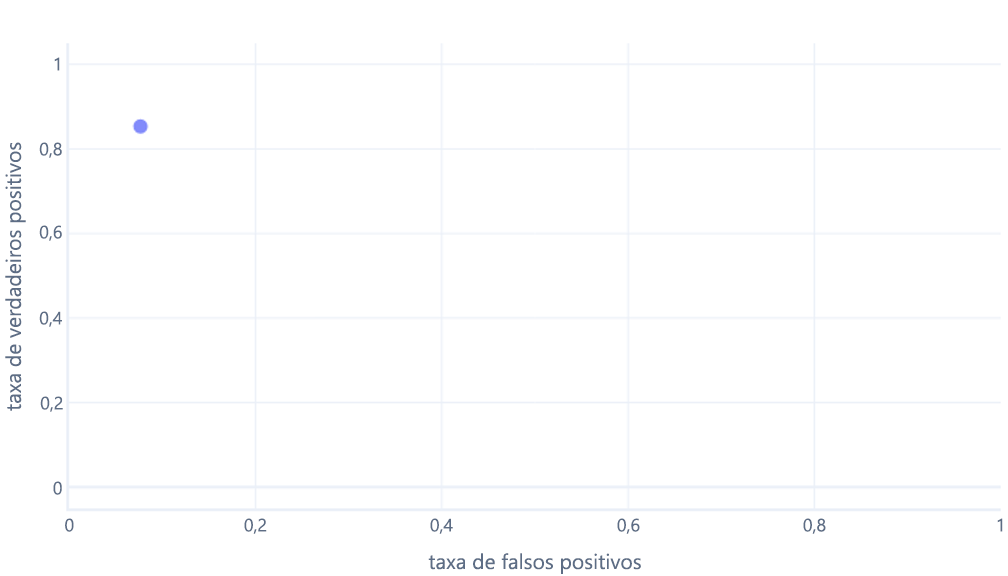
Se você também está pensando assim, acertou. Um modelo treinado só produz um ponto. No entanto, lembre-se de que os modelos têm um limite, normalmente de 50%, que é usado para decidir entre usar o rótulo verdadeiro (caminhante) ou o rótulo falso (árvore). Se alterarmos esse limite para 30% e recalcularmos as taxas de verdadeiros positivos e falsos positivos, obteremos outro ponto:
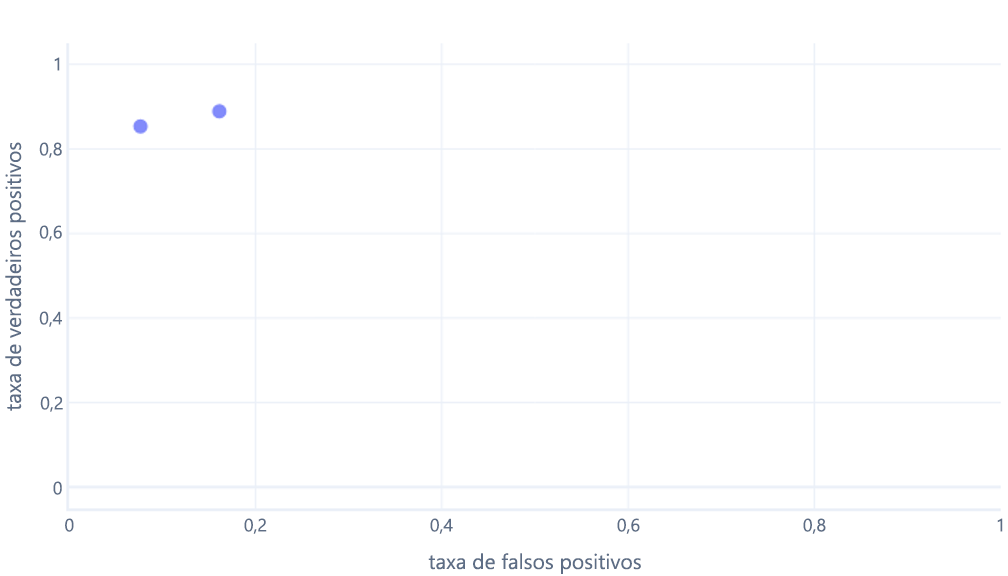
Se isso for feito para os limites entre 0% a 100%, será possível obter um grafo como este:
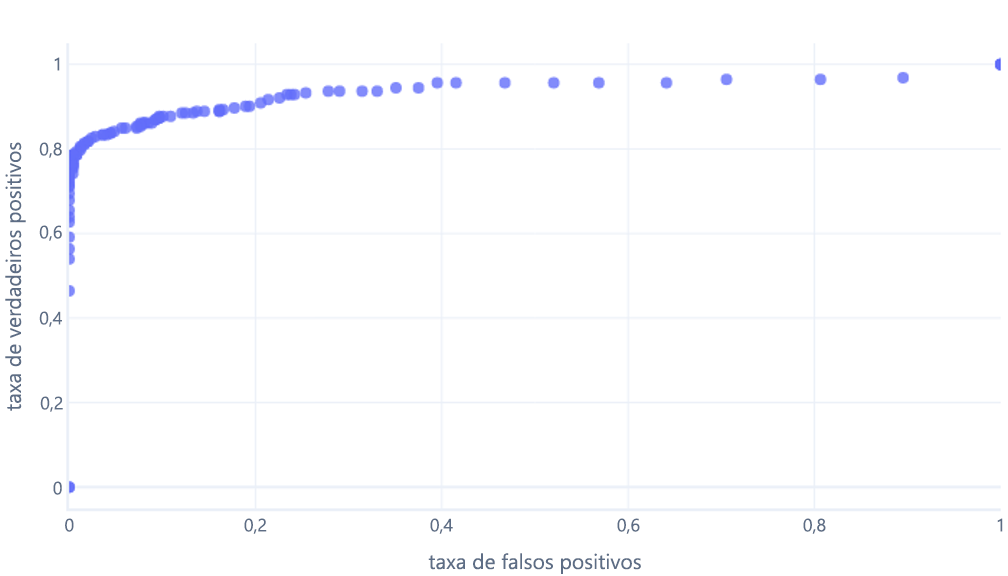
O que geralmente exibimos como uma linha:
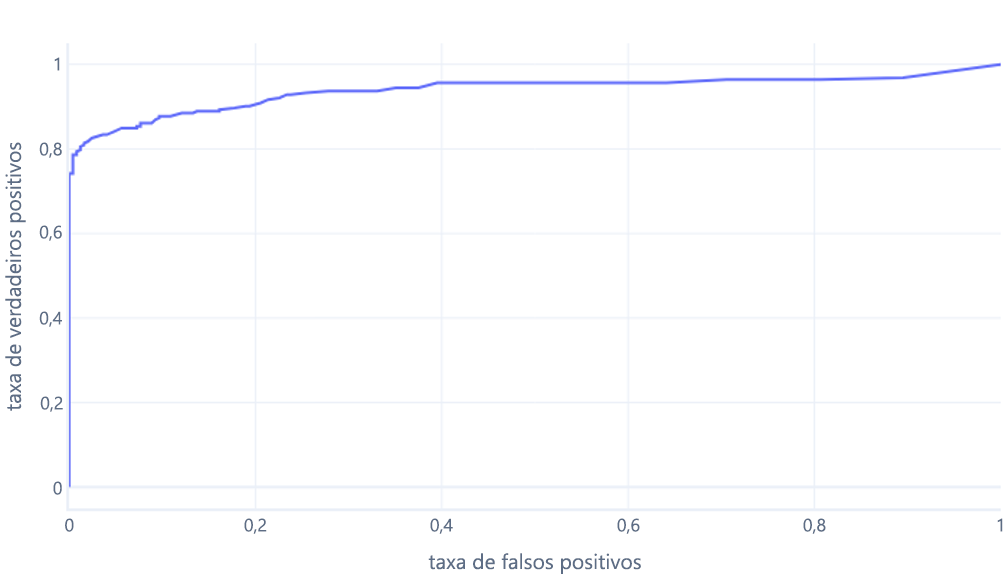
O segundo motivo pelo qual esses grafos podem ser confusos é o jargão envolvido. Lembre-se de que queremos uma alta taxa de verdadeiros positivos (identificar caminhantes como tal) e uma baixa taxa de falsos positivos (não identificar árvores como caminhantes).
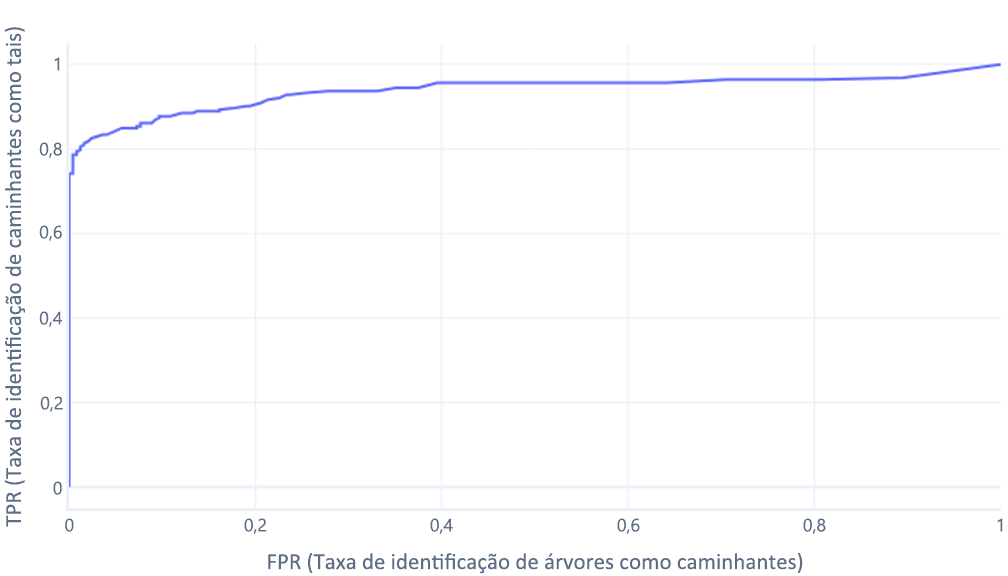
ROC bom, ROC ruim
Entender as curvas ROC que são boas e ruins é algo que é mais bem feito em um ambiente interativo. Quando estiver pronto, vá para o próximo exercício a fim de explorar este tópico.