Comparar e otimizar as curvas ROC
As curvas ROC (características de operação do receptor) permitem comparar modelos entre si e ajustar o modelo selecionado. Veja a seguir como e por que isso é feito.
Como ajustar um modelo
O uso mais óbvio de uma curva ROC é escolher um limite de decisão que ofereça o melhor desempenho. Lembre-se de que os modelos nos fornecem probabilidades, como uma probabilidade de 65% de que o exemplo é um caminhante. O limite de decisão é o ponto acima do qual um exemplo recebe a atribuição de verdadeiro (caminhante) ou abaixo do qual recebe a atribuição de false (árvore). Se o limite de decisão fosse 50%, um percentual de 65% seria atribuído a “true” (caminhante). No entanto, se o limite de decisão fosse 70%, uma probabilidade de 65% seria muito pequena e receberia a atribuição de “false” (árvore).
Você viu no exercício anterior que, ao criar uma curva ROC, você simplesmente altera o limite de decisão e avalia quão bem o modelo funciona. Quando fazemos isso, podemos encontrar o limite que fornece os resultados ideais.
Normalmente, não há um só limite que forneça a melhor TPR (taxa de verdadeiros positivos) e a FPR (taxa de falsos positivos) mais baixa. Isso significa que o limite ideal depende do que você está tentando obter. Por exemplo, neste cenário, é muito importante ter uma alta taxa de verdadeiros positivos, pois se um caminhante não for identificado e uma avalanche ocorrer, a equipe não saberá que deve resgatá-lo. Apesar disso, há uma compensação: se a taxa de falsos positivos for muito alta, a equipe de resgate poderá ser enviada repetidas vezes para resgatar pessoas que simplesmente não existem. Em outras situações, a taxa de falsos positivos é considerada mais importante. Por exemplo, a área da ciência tem uma tolerância baixa para resultados falsos positivos. Se a taxa de falsos positivos de experimentos científicos for maior, haverá uma infinidade de afirmações contraditórias e será impossível entender o que é real.
Como comparar modelos com a AUC
É possível usar curvas ROC para comparar modelos entre si, assim como é feito com funções de custo. Uma curva ROC de um modelo mostra o desempenho dele em uma variedade de limites de decisão. No final das contas, o mais importante em um modelo é saber qual será o desempenho dele no mundo real, em que há apenas um limite de decisão. Então, por que comparar modelos usando limites que nunca serão usados? Há duas respostas para isso.
Em primeiro lugar, comparar as curvas ROC de maneiras específicas é como executar um teste estatístico que nos diz se um modelo se saiu melhor nesse conjunto de teste específico e se é provável que ele continue tendo um desempenho melhor no futuro. Isso não será abordado neste material de aprendizagem, mas vale a pena tê-lo em mente.
Em segundo lugar, a curva ROC mostra, até certo grau, a dependência do modelo em ter o limite perfeito. Por exemplo, se o modelo só tiver um bom desempenho quando tivermos um limite de decisão igual a 0,9, mas muito acima ou abaixo desse valor, esse não será um bom design. Você provavelmente preferiria trabalhar com um modelo que funcionasse razoavelmente bem para vários limites porque saberia que, se os dados reais recebidos fossem ligeiramente diferentes daqueles no conjunto de teste, o desempenho do modelo não necessariamente seria muito prejudicado.
Como comparar os ROCs?
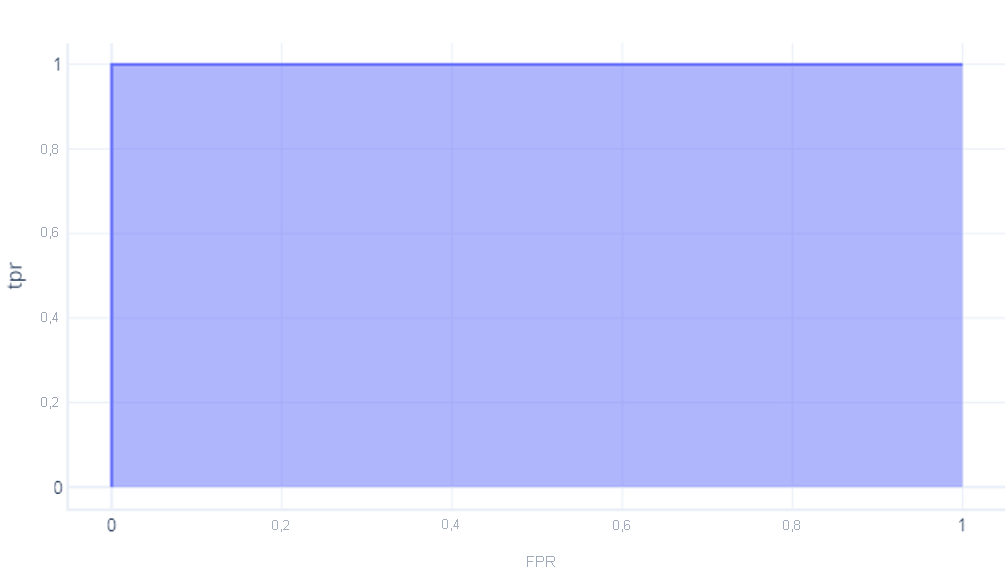
A maneira mais fácil de comparar os ROCs numericamente é usando a AUC (área sob a curva). Literalmente, essa é a área do grafo que fica abaixo da curva. Por exemplo, o modelo perfeito do último exercício tem uma AUC igual a 1:
No entanto, esse modelo que não teve um desempenho melhor do que um palpite tem uma área de cerca de 0,5:
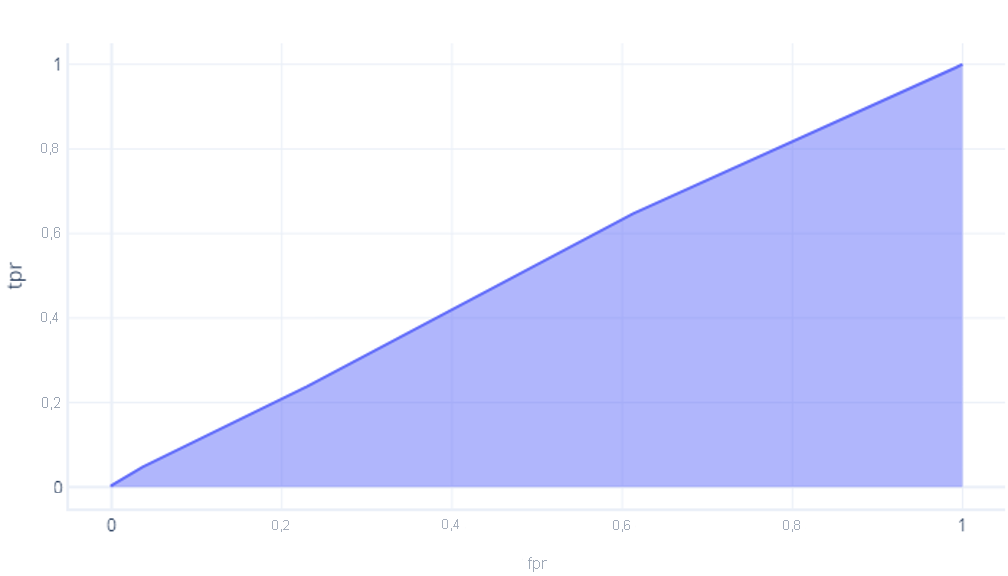
Quanto mais perfeito for um modelo, maior será essa área. Se tivermos um modelo com uma AUC grande, sabemos que ele funcionará bem para vários limites e, portanto, provavelmente tem uma boa arquitetura e foi bem treinado. Por outro lado, um modelo com uma AUC pequena (mais próxima de 0,5) não funciona bem.