Regressão linear múltipla e R-quadrado

• 4 minutos

Nesta unidade, vamos comparar a regressão linear múltipla com aregressão linear simples. Também vamos analisar uma métrica chamada R², que costuma ser usada para avaliar a qualidade de um modelo de regressão linear.

Regressão linear múltipla

A regressão linear múltipla modela a relação entre vários recursos e uma variável. Matematicamente, ela é o mesmo que uma regressão linear simples, e costuma ser ajustada usando a mesma função de custo, mas com mais recursos.

Em vez de modelar uma relação única, essa técnica modela simultaneamente várias relações, que ela trata como independentes umas das outras. Por exemplo, se estamos prevendo a gravidade da doença de um cachorro com base na sua idade e no seu percentual_de_gordura_corporal, encontramos duas relações:

• Como a idade aumenta ou diminui a doença
• Como o percentual_de_gordura_corporal aumenta ou diminui a doença

Se estivermos trabalhando com apenas dois recursos, poderemos visualizar nosso modelo como um plano — superfície 2D plana — assim como podemos modelar a regressão linear simples como uma linha. Exploraremos isso no próximo módulo.

A regressão linear múltipla tem pressupostos

O fato de que o modelo espera que os recursos sejam independentes é chamado de pressuposto do modelo. Quando os pressupostos de um modelo não são verdadeiros, o modelo pode fazer previsões enganosas.

Por exemplo, a idade provavelmente prevê como os cães adoecem, já que cães mais velhos adoecem mais. Ela pode prever também se os cães sabem jogar frisbee; os cães mais velhos provavelmente já sabem jogar frisbee. Se incluíssemos idade e saber_jogar_frisbee como recursos em nosso modelo, ele provavelmente nos informaria que saber_jogar_frisbee é um bom indicador de doenças e subestimaria a importância da idade. Isso é meio absurdo, porque saber jogar frisbee não causa doenças. Por outro lado, raça_do_cachorro também pode ser um bom indicador de doenças, mas não há razões para acreditar que a idade possa prever a raça_do_cachorro. Portanto, é seguro incluir ambos em um modelo.

Bondade de ajuste: R²

Sabemos que as funções de custo podem ser usadas para avaliar se um modelo se ajusta bem aos dados nos quais é treinado. Os modelos de regressão linear têm uma medida especial relacionada chamada R² (R-quadrado). R² é um valor entre 0 e 1 que nos informa como um modelo de regressão linear se ajusta aos dados. Quando se fala em fortes correlações, isso costuma significar que o valor de R² foi alto.

O R² requer matemática que vai além do que pretendemos abordar neste curso, mas podemos pensar nela de forma intuitiva. Vamos considerar o exercício anterior, em que examinamos a relação entre idade e temperatura_interna. Um R² de 1 significaria que a idade medida em anos pôde ser usada para prever com perfeição quem tinha temperatura alta ou baixa. Por outro lado, um 0 significaria que não havia qualquer relação entre o número de anos e a temperatura.

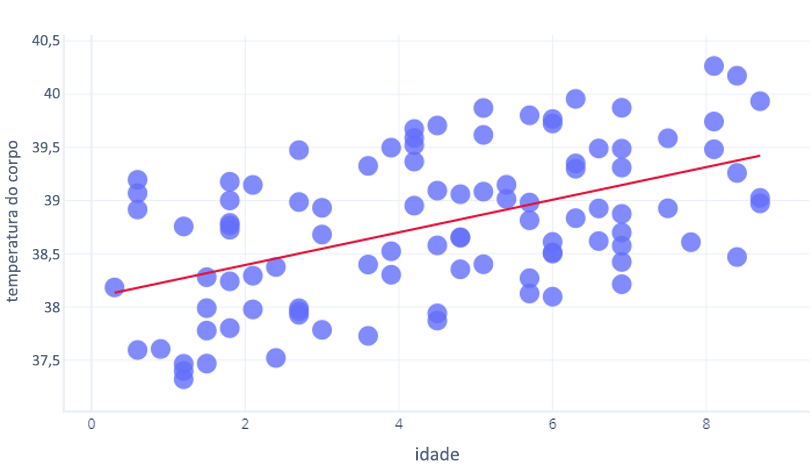
A realidade está em algum ponto desse intervalo. Nosso modelo poderia prever a temperatura até certo modo (portanto, é melhor do que R² = 0), mas os pontos variaram em relação a essa previsão (portanto, o modelo é menor que R²= 1).

O R² é só a metade da história.

Os valores de R² são amplamente aceitos, mas não são uma medida perfeita que podemos usar de maneira isolada. Ele sofre quatro limitações:

• Devido à forma como o R² é calculado, quanto mais amostras tivermos, mais alto será o R². Isso pode nos levar a achar que um modelo é melhor do que outro modelo idêntico simplesmente porque os valores de R² foram calculados usando quantidades diferentes de dados.
• Os valores de R² não nos dizem como um modelo vai funcionar com dados novos e ainda não vistos. Os estatísticos contornam isso calculando uma medida suplementar, chamada valor-p, que não abordaremos aqui. No aprendizado de máquina, costumamos, em vez disso, testar nosso modelo explicitamente com outro conjunto de dados.
• Os valores de R² não mostram a direção da relação. Por exemplo, um valor de R² de 0,8 não informa se a linha é inclinada para cima ou para baixo. Ele também não informa a inclinação da linha.

Também vale a pena ter em mente que não há critérios universais para o que torna um valor R² "bom o suficiente". Por exemplo, na maior parte da física, é improvável que correlações que não sejam muito próximas de 1 sejam consideradas úteis, mas ao modelar sistemas complexos, valores de R² tão baixos quanto 0,3 podem ser considerados excelentes.