series_fit_poly()
Область применения: ✅Microsoft Fabric✅Azure Data Explorer✅Azure Monitor✅Microsoft Sentinel
Применяет полиномиальную регрессию из независимой переменной (x_series) к зависимой переменной (y_series). Эта функция принимает таблицу, содержащую несколько рядов (динамические числовые массивы) и создает наиболее подходящий полиномический многоном для каждой серии с помощью полиномиальной регрессии.
Совет
- Для линейной регрессии равномерного распределения рядов, созданных оператором make-series, используйте более простую функцию series_fit_line(). См . пример 2.
- Если x_series предоставляется, а регрессия выполняется для высокой степени, рассмотрите возможность нормализации в диапазоне [0-1]. См . пример 3.
- Если x_series имеет тип datetime, его необходимо преобразовать в двойной и нормализованный. См . пример 3.
- Эталонная реализация полиномиальной регрессии с помощью встроенного Python см. в разделе series_fit_poly_fl().
Синтаксис
T | extend series_fit_poly( y_series [, степень x_series, ])
Дополнительные сведения о соглашениях синтаксиса.
Параметры
| Имя (название) | Type | Обязательно | Описание |
|---|---|---|---|
| y_series | dynamic |
✔️ | Массив числовых значений, содержащих зависимые переменные. |
| x_series | dynamic |
Массив числовых значений, содержащий независимую переменную. Требуется только для неравномерно размеченных рядов. Если он не указан, он имеет значение по умолчанию [1, 2, ..., length(y_series)]. | |
| градус | Обязательный порядок полиномиального соответствия. Например, 1 для линейной регрессии, 2 для квадратной регрессии и т. д. Значение по умолчанию — 1, указывающее линейную регрессию. |
Возвраты
Функция series_fit_poly() возвращает следующие столбцы:
rsquare: r-квадрат является стандартной мерой качества соответствия. Значение является числом в диапазоне [0–1], где 1 — лучше всего подходит, и 0 означает, что данные не упорядочены и не соответствуют какой-либо строке.coefficients: числовый массив, содержащий коэффициенты наиболее подходящего полиномиального с заданной степенью, упорядоченный от самого высокого коэффициента питания до наименьшего.variance: вариативность зависимой переменной (y_series).rvariance: остаточная дисперсия, которая является дисперсией между входными значениями данных, которые являются приблизительными.poly_fit: числовый массив, содержащий ряд значений наиболее подходящих полиномиальных значений. Длина ряда равна длине зависимой переменной (y_series). Значение, используемое для диаграммы.
Примеры
Пример 1
Пятый порядок полиномиал с шумом на осях x и y:
range x from 1 to 200 step 1
| project x = rand()*5 - 2.3
| extend y = pow(x, 5)-8*pow(x, 3)+10*x+6
| extend y = y + (rand() - 0.5)*0.5*y
| summarize x=make_list(x), y=make_list(y)
| extend series_fit_poly(y, x, 5)
| project-rename fy=series_fit_poly_y_poly_fit, coeff=series_fit_poly_y_coefficients
|fork (project x, y, fy) (project-away x, y, fy)
| render linechart
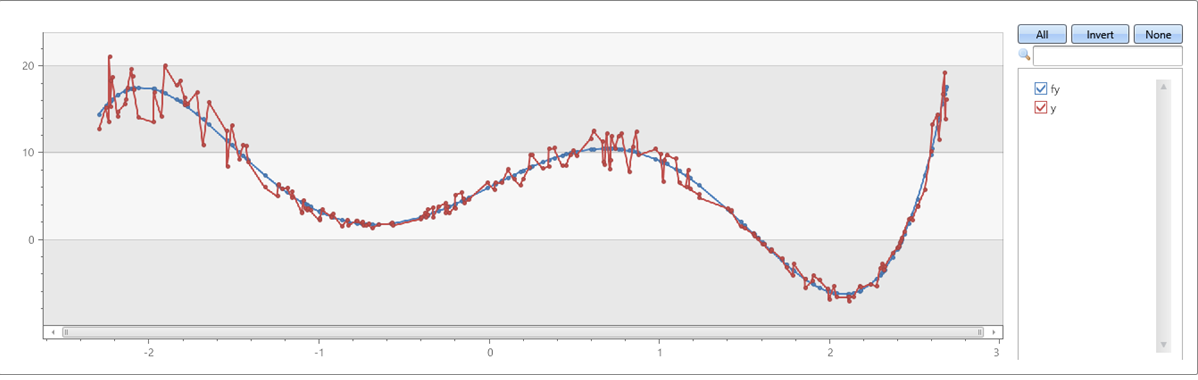
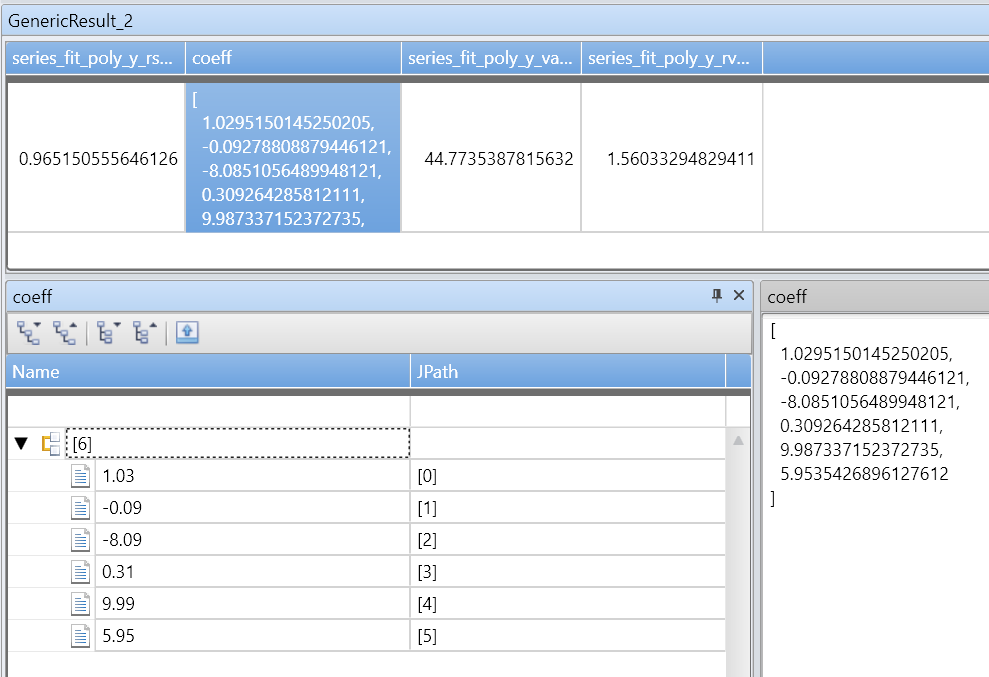
Пример 2
Убедитесь, что series_fit_poly с соответствием degree=1 series_fit_line:
demo_series1
| extend series_fit_line(y)
| extend series_fit_poly(y)
| project-rename y_line = series_fit_line_y_line_fit, y_poly = series_fit_poly_y_poly_fit
| fork (project x, y, y_line, y_poly) (project-away id, x, y, y_line, y_poly)
| render linechart with(xcolumn=x, ycolumns=y, y_line, y_poly)
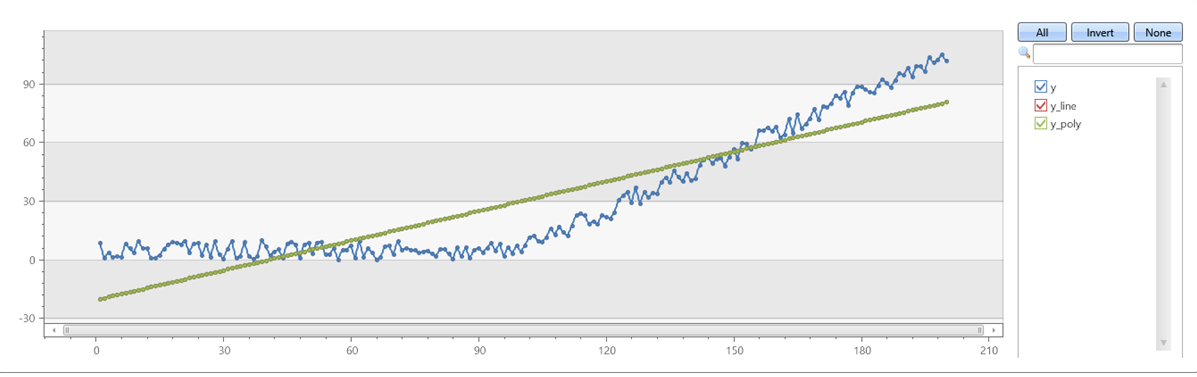

Пример 3
Нерегулярные (неравномерно размеченные) временные ряды:
//
// x-axis must be normalized to the range [0-1] if either degree is relatively big (>= 5) or original x range is big.
// so if x is a time axis it must be normalized as conversion of timestamp to long generate huge numbers (number of 100 nano-sec ticks from 1/1/1970)
//
// Normalization: x_norm = (x - min(x))/(max(x) - min(x))
//
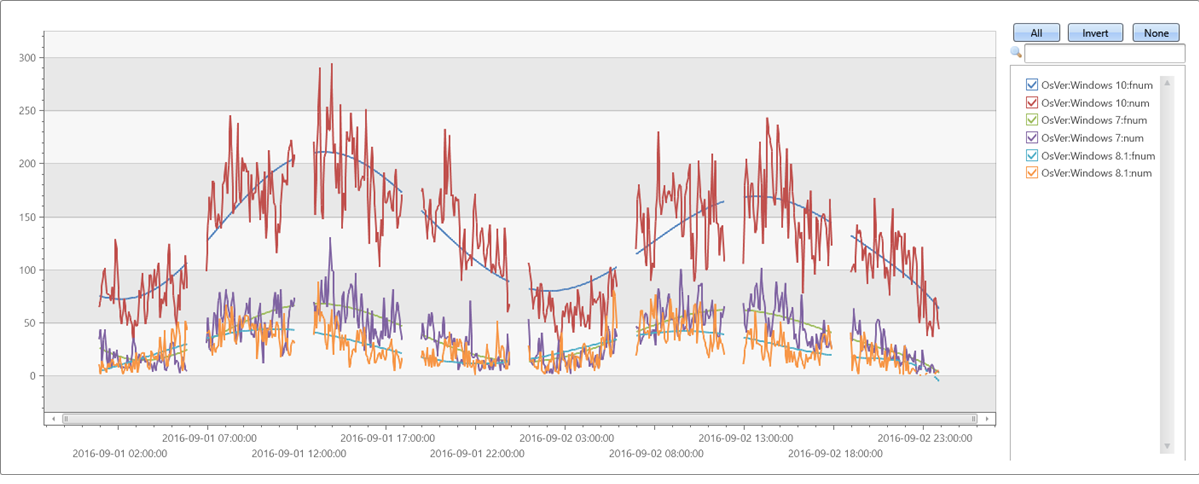
irregular_ts
| extend series_stats(series_add(TimeStamp, 0)) // extract min/max of time axis as doubles
| extend x = series_divide(series_subtract(TimeStamp, series_stats__min), series_stats__max-series_stats__min) // normalize time axis to [0-1] range
| extend series_fit_poly(num, x, 8)
| project-rename fnum=series_fit_poly_num_poly_fit
| render timechart with(ycolumns=num, fnum)