量子運算中的量子位
正如位元是傳統運算中的基礎資訊物件,Q 位元 (量子位元) 則是量子運算的基礎資訊物件。 為了瞭解此對應,本文將探討最簡單的範例:單一量子位。
表示量子位
雖然位或二進位數位可以有 0 或 1 的值,但量子位可以有$值為 0$、$1 或量子迭加 $0$$ 和 $1。$$$$$
單一量子位的狀態可由單位常態的二維數據行向量來描述,也就是說,其專案的大小平方必須加總到 $1$。 這個向量稱為量子狀態向量,會保存描述單一量子位量子系統所需的所有資訊,就像單一位保存描述二進位變數狀態所需的所有資訊一樣。 如需量子運算中向量和矩陣的基本概念,請參閱 向量和矩陣。
具有 norm $1$ 之實際或複數的任何二維數據行向量都代表量子位持有的可能量子狀態。 因此$\begin{bmatrix}\end{bmatrix}$\\\alpha\beta,如果和 $\beta$ 是滿足 $|\alpha|^2 + |\beta|^2 = 1$ 的複數,則表示量子位狀態。$\alpha$ 代表量子位的有效量子狀態向量範例包括
$$\begin{bmatrix}1 \\ 0\end{bmatrix}、 \begin{bmatrix} 0 \\ 1\end{bmatrix}、\\\frac{\begin{bmatrix}{1}{\sqrt{2}}{1}{\sqrt{2}}\end{bmatrix}\frac{、、\begin{bmatrix}\frac{1}{\sqrt{{2}}\frac{\end{bmatrix}{-1}{\sqrt{2}}\\\text{ 和{2}}}\begin{bmatrix}\frac{\frac{1}{\sqrt{\\ i。}{\sqrt{2}}\end{bmatrix}$$
量子狀態向量 $\begin{bmatrix} 1 \\ 0 \end{bmatrix}$ 和 $\begin{bmatrix} 0 \\ 1 \end{bmatrix}$ 扮演特殊角色。 這兩個向量會形成描述量子位狀態的向量空間基礎。 這表示任何量子狀態向量都可以撰寫為這些基礎向量的總和。 具體而言,向量 $\begin{bmatrix} x y \end{bmatrix}$ 可以寫入為 $x \begin{bmatrix} \\ 1 \\ 0 \end{bmatrix} + y \begin{bmatrix} 0 \\ 1 \end{bmatrix}$。 雖然這些向量的任何旋轉都會作為量子位的完全有效基礎,但藉由呼叫量子位來選擇這個特定量子位。
這兩個量子狀態是用來對應至傳統位的兩個狀態,即 $0$ 和 $1$。 標準慣例是選擇
$$0\equiv\begin{bmatrix} 1 \\ 0 \end{bmatrix}, \qquad 1 \equiv\begin{bmatrix} 0 \\ 1 \end{bmatrix},$$
雖然同樣可以採取相反的選擇。 因此,在可能的單一量子位量子狀態向量的無限數目中,只有兩個對應至傳統位的狀態:所有其他量子狀態都不會。
測量量子位
如何說明量子位,可以藉由討論測量概念來取得這些狀態所代表的一些直覺。 測量相當於「查看」量子位的非正式概念,其會立即將量子狀態折疊為兩個傳統狀態 $\begin{bmatrix} 1 \\ 0 \end{bmatrix}$ 或 $\begin{bmatrix} 0 \\ 1 \end{bmatrix}$的其中一個。 測量量子狀態向量$\begin{bmatrix}\end{bmatrix}$\beta\\\alpha指定的量子位時,結果 $0$ 會以機率 $|\alpha|^2$ 取得,而結果 $1$ 則為 probability $|\beta|^2。$ 在結果 $0 上,量子位的新狀態為 $\begin{bmatrix} 1 0\end{bmatrix}$;在結果 $1$ \\ 上,其狀態為 $\begin{bmatrix} 0 \\ 1 \end{bmatrix}$。$ 請注意,由於正規化條件 ^2 + |\beta|^2 = 1,這些機率最多可加總 $1$$。$|\alpha|
測量的屬性也表示量子狀態向量的整體標誌無關。 否定向量相當於 $\alpha\right箭號 -\alpha$ 和 $\beta\right箭號 -\beta$ 。 由於測量 $0$ 和 $1$ 的機率取決於詞彙的大小平方,因此插入這類符號並不會改變機率。 這類階段通常稱為 "global phases"而且更通常可以是 e^{i \phi}$ 格式$,而不只是 $\pm 1$。
測量的最終重要屬性是,它不一定會損害所有量子狀態向量。 如果一個從狀態 $\begin{bmatrix} 1 \\ 0 中的量子位開始,這會對應至傳統狀態 $0\end{bmatrix}$,則測量此狀態一律會產生結果 $0$$,並將量子狀態維持不變。 從這個意義上說,如果只有傳統位(例如,1 \\ 0 \end{bmatrix}$ 或 $\begin{bmatrix}0 \\ 1 \end{bmatrix}$的量子位$\begin{bmatrix}),則測量不會損害系統。 這表示一個人可以在量子計算機上復寫傳統數據,並在量子計算機上操作它,就像在傳統計算機上一樣。 不過,一次將資訊儲存在兩種狀態的能力,就是將量子運算提升到傳統化之外,並進一步搶佔量子計算機不分青紅皂白地複製量子數據的能力,另 請參閱無複制定理。
使用 Bloch 球體可視化量子位和轉換
量子位也可以使用 Bloch 圓球表示法,以 $3D$ 來描繪。 Bloch 球可讓您將單一量子位量子狀態(這是二維複雜向量)描述為三維實值向量。 這很重要,因為它可讓我們可視化單一量子位狀態,進而開發理解多量子位狀態的寶貴推理(可悲的是 Bloch 球體表示法中斷)。 Bloch 球體可以可視化,如下所示:
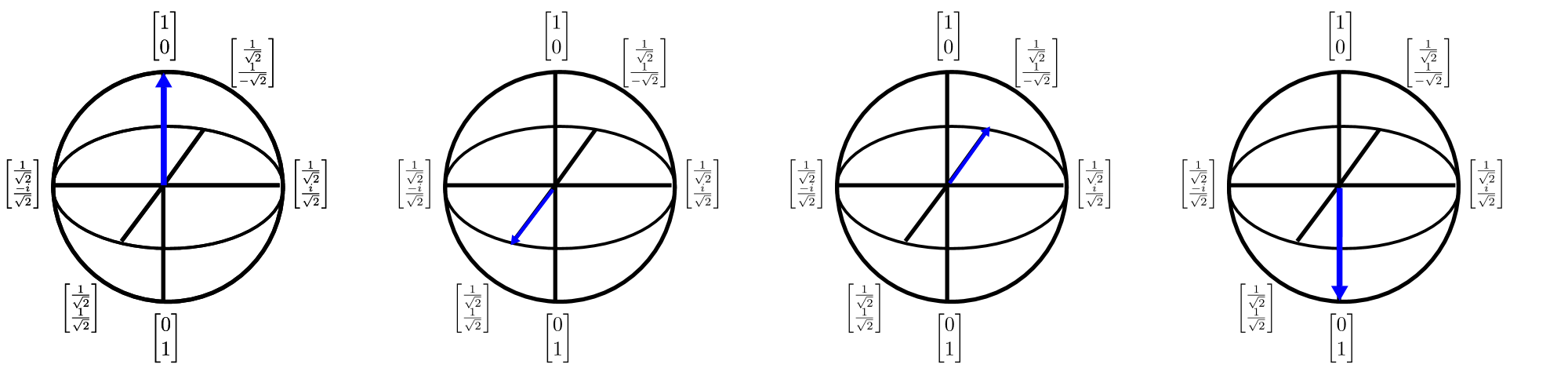
此圖表中的箭號會顯示量子狀態向量指向的方向,而箭號的每個轉換都可以視為一個基數座標軸的旋轉。 雖然將量子計算視為一連串旋轉是一種強大的直覺,但使用此直覺來設計和描述演算法是一項挑戰。 Q# 藉由提供描述這類輪替的語言來減輕此問題。
單一量子位作業
量子計算機會套用一組通用量子網關來處理數據,以模擬量子狀態向量的任何旋轉。 這種通用概念類似於傳統(例如傳統)運算的普遍性概念,如果輸入位的每個轉換都可以使用有限長度電路來執行,網關集就會被視為通用。 在量子運算中,我們允許在量子位上執行的有效轉換是單一轉換和測量。 相鄰 運算 或複雜串連轉置對於量子運算至關重要,因為它需要反轉量子轉換。
單一量子位作業或單一量子位量子網關可分為兩個類別:Clifford 閘道和非 Clifford 閘道。 非克利福德門只 $包含 T$ 門(也稱為 $\pi/8$ 門)。
$$T=\begin{bmatrix} 1 amp; 0 0 &\\ amp; e^{i\pi/4\end{bmatrix}}.& $$
默認包含在 中的 Q#單一量子位 Clifford 閘道標準集合包括
$$H=\frac{{1}{\sqrt{{2}}\begin{bmatrix} 1 & 1 \\ 1 &-1 , \qquad S =\begin{bmatrix} 1 \end{bmatrix} & 0 0 \\ amp; i \end{bmatrix}= T^2, \qquad X=\begin{bmatrix} 0 &&1 1 \\& 0 \end{bmatrix}= HT^4H,$$
$$Y =0 amp; -i &\\ amp; 0 \end{bmatrix}=T^2HT^4 HT^6, \qquad Z=\begin{bmatrix}1&&\begin{bmatrix}0 0\\& amp;-1 \end{bmatrix}=T^4。 $$
在這裡,作業 $X$、 $Y$ 和 $Z$ 特別頻繁使用,並以其創作者沃爾夫岡·保利的名字命名 為 Pauli 運算符 。 這些作業可以與非 Clifford 閘道( $T-gate$)一起組成,以近似單一量子位的任何單一轉換。
雖然先前是用來描述堆棧邏輯層級作業的最常用基本網關(將邏輯層級視為量子演算法的層級),但通常很方便地考慮演算法層級的基本作業,例如,更接近函式描述層級的作業。 幸運的是, Q# 也有方法可用來實作較高層級的一元式,進而允許實作高階演算法,而不會明確地分解所有專案到 Clifford 和 $T-gates$。
最簡單的這類基本類型是單一量子位旋轉。 一般會考慮三個單一量子位旋轉: $R_x$、 $R_y$ 和 $R_z$。 例如,若要可視化旋轉$R_x(\theta)$的動作,想像一下,將右拇指指向 Bloch 球體 X$ 軸的方向$,並透過 \theta/2$ 弧度的角度$旋轉向量。 這種令人困惑的 $2$ 因素源於在 Bloch 球體上繪製時,正交向量 $相隔 180^\circ$ ,但實際上 $以幾何方式相隔 90^\circ$ 度。 對應的單一矩陣如下:
\begin{align*}&R_z(\theta) e^-i\theta Z/2 e^{-i\theta/2\begin{bmatrix}}= amp; 0 0&\\ amp; e^{i\theta/2}\end{bmatrix}}&, \\&{=R_x(\theta) e^{-i\theta X/2=} HR_z(\theta)H =\begin{bmatrix} \cos(\theta/2) & -i\sin(\theta/2)\\ -i\sin(\theta/2) amp; \cos(\theta/2) \end{bmatrix}&, \\& =R_y(\theta) e^-i\theta Y/2}= SHR_z(\theta)HS^\begin{bmatrix}=\dagger \cos(\theta/2&) amp; -\sin(\theta/2) \sin(\theta/2)\\ & \cos(\theta/2) 。 \end{bmatrix}{= \end{對齊*}
就像任何三個旋轉都可以結合在一起,以在三個維度中執行任意旋轉一樣,從 Bloch 球體表示中可以看到任何一元矩陣也可以撰寫為三個旋轉序列。 具體來說,對於每個單一矩陣 $U$ 都有 $\alpha,\beta因此\gamma\delta$$ U=^{i\alpha} R_x()R_z(\beta\gamma)R_x(\delta)。$ 因此 $,R_z(\theta)$ 和 $H$ 也會形成通用閘道集,雖然它不是離散集合,因為 $\theta$ 可以接受任何值。 因此,由於量子模擬中的應用程式,這類連續網關對於量子計算至關重要,特別是在量子演算法設計層級。 為了達成容錯硬體實作,它們最終會編譯成接近這些輪替的離散網關序列。