Application de transformations dans Direct2D

Dans Dessin avec Direct2D, nous avons vu que la méthode ID2D1RenderTarget::FillEllipse dessine une ellipse alignée sur les axes x et y. Mais supposons que vous vouliez dessiner une ellipse inclinée à un angle ?

En utilisant des transformations, vous pouvez modifier une forme des manières suivantes.

• Rotation autour d’un point.
• Mise à l’échelle
• Traduction (déplacement dans le sens X ou Y).
• Skew (également appelé cisaillement).

Une transformation est une opération mathématique qui mappe un ensemble de points à un nouvel ensemble de points. Par exemple, le diagramme suivant montre un triangle pivoté autour du point P3. Une fois la rotation appliquée, le point P1 est mappé à P1', le point P2 est mappé à P2', et le point P3 est mappé à lui-même.

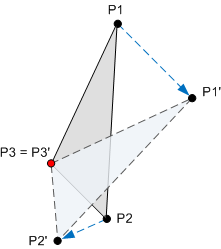
Les transformations sont implémentées à l’aide de matrices. Toutefois, vous n’avez pas besoin de comprendre les mathématiques des matrices pour les utiliser. Si vous souhaitez en savoir plus sur les mathématiques, consultez Annexe : Transformations matricielles.

Pour appliquer une transformation dans Direct2D, appelez la méthode ID2D1RenderTarget::SetTransform . Cette méthode prend une structure D2D1_MATRIX_3X2_F qui définit la transformation. Vous pouvez initialiser cette structure en appelant des méthodes sur la classe D2D1::Matrix3x2F . Cette classe contient des méthodes statiques qui retournent une matrice pour chaque type de transformation :

• Matrix3x2F::Rotation
• Matrix3x2F::Scale
• Matrix3x2F::Translation
• Matrix3x2F::Skew

Par exemple, le code suivant applique une rotation de 20 degrés autour du point (100, 100).

pRenderTarget->SetTransform(
    D2D1::Matrix3x2F::Rotation(20, D2D1::Point2F(100,100)));

La transformation est appliquée à toutes les opérations de dessin ultérieures jusqu’à ce que vous appeliez à nouveau SetTransform . Pour supprimer la transformation actuelle, appelez SetTransform avec la matrice d’identité. Pour créer la matrice d’identité, appelez la fonction Matrix3x2F::Identity .

pRenderTarget->SetTransform(D2D1::Matrix3x2F::Identity());

Dessin des aiguilles de l’horloge

Mettons les transformations à utiliser en convertissant notre programme Circle en horloge analogique. Nous pouvons le faire en ajoutant des lignes pour les mains.

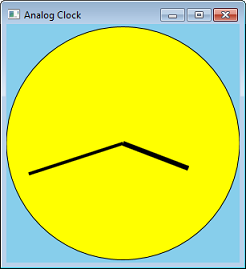
Au lieu de calculer les coordonnées des lignes, nous pouvons calculer l’angle, puis appliquer une transformation de rotation. Le code suivant montre une fonction qui dessine une aiguille d’horloge. Le paramètre fAngle donne l’angle de la main, en degrés.

void Scene::DrawClockHand(float fHandLength, float fAngle, float fStrokeWidth)
{
    m_pRenderTarget->SetTransform(
        D2D1::Matrix3x2F::Rotation(fAngle, m_ellipse.point)
            );

    // endPoint defines one end of the hand.
    D2D_POINT_2F endPoint = D2D1::Point2F(
        m_ellipse.point.x,
        m_ellipse.point.y - (m_ellipse.radiusY * fHandLength)
        );

    // Draw a line from the center of the ellipse to endPoint.
    m_pRenderTarget->DrawLine(
        m_ellipse.point, endPoint, m_pStroke, fStrokeWidth);
}

Ce code dessine une ligne verticale, commençant du centre de la face de l’horloge et se terminant au point point endPoint. La ligne est pivotée autour du centre de l’ellipse en appliquant une transformation de rotation. Le point central de la rotation est le centre de l’ellipse qui forme la face de l’horloge.

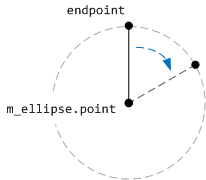
Le code suivant montre comment toute la face de l’horloge est dessinée.

void Scene::RenderScene()
{
    m_pRenderTarget->Clear(D2D1::ColorF(D2D1::ColorF::SkyBlue));

    m_pRenderTarget->FillEllipse(m_ellipse, m_pFill);
    m_pRenderTarget->DrawEllipse(m_ellipse, m_pStroke);

    // Draw hands
    SYSTEMTIME time;
    GetLocalTime(&time);

    // 60 minutes = 30 degrees, 1 minute = 0.5 degree
    const float fHourAngle = (360.0f / 12) * (time.wHour) + (time.wMinute * 0.5f);
    const float fMinuteAngle =(360.0f / 60) * (time.wMinute);

    DrawClockHand(0.6f,  fHourAngle,   6);
    DrawClockHand(0.85f, fMinuteAngle, 4);

    // Restore the identity transformation.
    m_pRenderTarget->SetTransform( D2D1::Matrix3x2F::Identity() );
}

Vous pouvez télécharger le projet Visual Studio complet à partir de l’exemple d’horloge Direct2D. (Juste pour le plaisir, la version de téléchargement ajoute un gradiant radial à la face de l’horloge.)

Combinaison de transformations

Les quatre transformations de base peuvent être combinées en multipliant deux matrices ou plus. Par exemple, le code suivant combine une rotation avec une traduction.

const D2D1::Matrix3x2F rot = D2D1::Matrix3x2F::Rotation(20);
const D2D1::Matrix3x2F trans = D2D1::Matrix3x2F::Translation(40, 10);

pRenderTarget->SetTransform(rot * trans);

La classe Matrix3x2F fournit operator*() pour la multiplication de matrice. L’ordre dans lequel vous multipliez les matrices est important. La définition d’une transformation (M × N) signifie « Appliquer D’abord M, suivi de N ». Par exemple, voici la rotation suivie de la traduction :

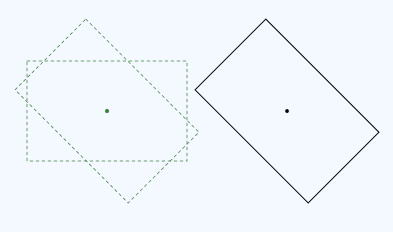
Voici le code de cette transformation :

const D2D1::Matrix3x2F rot = D2D1::Matrix3x2F::Rotation(45, center);
const D2D1::Matrix3x2F trans = D2D1::Matrix3x2F::Translation(x, 0);
pRenderTarget->SetTransform(rot * trans);

Maintenant, comparez cette transformation à une transformation dans l’ordre inverse, traduction suivie d’une rotation.

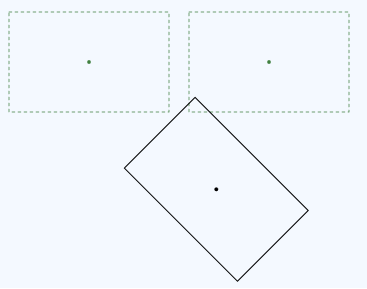
La rotation est effectuée autour du centre du rectangle d’origine. Voici le code de cette transformation.

D2D1::Matrix3x2F rot = D2D1::Matrix3x2F::Rotation(45, center);
D2D1::Matrix3x2F trans = D2D1::Matrix3x2F::Translation(x, 0);
pRenderTarget->SetTransform(trans * rot);

Comme vous pouvez le voir, les matrices sont les mêmes, mais l’ordre des opérations a changé. Cela se produit parce que la multiplication matricielle n’est pas commutative : M × N ≠ N × M.

Suivant

Annexe : Transformations matricielles