Panoramica delle trasformazioni
Le trasformazioni della matrice gestiscono molti calcoli matematici di basso livello della grafica 3D.
Il processo geometrico accetta vertici come input. Il motore di trasformazione applica le trasformazioni di mondo, visualizzazione e proiezione ai vertici, ritaglia il risultato e passa tutto al rasterizzatore.
| Trasformazione e spazio | Descrizione |
|---|---|
| Coordinate del modello nello spazio del modello | All'inizio della pipeline, i vertici di un modello vengono dichiarati rispetto a un sistema di coordinate locale. Si tratta di un'origine locale e di un orientamento. Questo orientamento delle coordinate viene spesso definito spazio del modello. Le singole coordinate sono denominate coordinate del modello. |
| Trasformazione globale nello spazio globale | La prima fase del processo geometrico trasforma i vertici di un modello da un sistema di coordinate locale a un sistema di coordinate utilizzato da tutti gli oggetti in una scena. Il processo di riorientamento dei vertici è denominato Trasformazione globale, che converte dallo spazio del modello a un nuovo orientamento denominato Spazio globale . Ogni vertice nello spazio globale viene dichiarato usando le Coordinate globali. |
| Trasforma la visualizzazione in spazio di visualizzazione (spazio della fotocamera) | Nella fase successiva, i vertici che descrivono il mondo 3D sono orientati rispetto a una fotocamera. In altre parole, l'applicazione sceglie un punto di vista per la scena e le coordinate dello spazio globale vengono spostate e ruotate intorno alla visualizzazione della fotocamera, trasformando lo spazio del mondo nello spazio di visualizzazione (noto anche come spazio della fotocamera). Questa è la Trasformazione della visualizzazione, che converte dallo spazio globale allo spazio di visualizzazione. |
| Trasformazione della proiezione in spazio di proiezione | La fase successiva è la Trasformazione della proiezione, che converte dallo spazio di visualizzazione allo spazio di proiezione. In questa parte della pipeline, gli oggetti vengono in genere ridimensionati in relazione alla loro distanza dal visualizzatore per dare l'illusione di profondità a una scena; gli oggetti vicini vengono creati per apparire più grandi rispetto agli oggetti distanti. Per semplicità, questa documentazione fa riferimento allo spazio in cui esistono vertici dopo la trasformazione della proiezione come Spazio di proiezione. Alcuni libri grafici potrebbero fare riferimento allo spazio di proiezione come spazio omogeneo post-prospettiva . Non tutte le trasformazioni di proiezione ridimensionano le dimensioni degli oggetti in una scena. Una proiezione come questa è talvolta detta proiezione affine or proiezione ortogonale. |
| Ritaglio nello spazio dello schermo | Nella parte finale della pipeline, tutti i vertici che non saranno visibili sullo schermo vengono rimossi, in modo che il rasterizzatore non prenda il tempo necessario per calcolare i colori e l'ombreggiatura per qualcosa che non verrà mai visto. Questo processo è denominato ritaglio. Dopo il ritaglio, i vertici rimanenti vengono ridimensionati in base ai parametri del riquadro di visualizzazione e convertiti in coordinate dello schermo. I vertici risultanti, visualizzati sullo schermo quando la scena viene rasterizzata, esistono nello spazio dello schermo. |
Le trasformazioni vengono usate per convertire la geometria dell'oggetto da uno spazio di coordinate a un altro. Direct3D usa matrici per eseguire trasformazioni 3D. Le matrici creano trasformazioni 3D. È possibile combinare matrici per produrre una singola matrice che include più trasformazioni.
È possibile trasformare le coordinate tra lo spazio del modello, lo spazio globale e lo spazio di visualizzazione.
- Trasformazione globale: converte dallo spazio del modello allo spazio globale.
- Visualizza trasformazione : converte dallo spazio globale allo spazio di visualizzazione.
- Trasformazione di proiezione: converte dallo spazio di visualizzazione allo spazio di proiezione.
Trasformazioni con matrice
Nelle applicazioni che usano una grafica 3D, è possibile usare trasformazioni geometriche per eseguire le operazioni seguenti:
- Esprimere la posizione di un oggetto rispetto a un altro oggetto.
- Ruotare e ridimensionare gli oggetti.
- Modificare le posizioni di visualizzazione, le direzioni e le prospettive.
È possibile trasformare qualsiasi punto (x,y,z) in un altro punto (x', y', z') usando una matrice 4x4, come illustrato nell'equazione seguente.
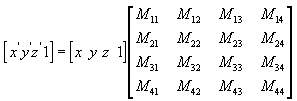
Eseguire le equazioni seguenti su (x, y, z) e la matrice per produrre il punto (x', y', z').
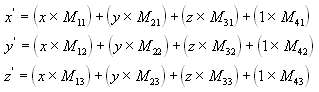
Le trasformazioni più comuni sono traslazione, rotazione e ridimensionamento. È possibile combinare le matrici che producono questi effetti in una singola matrice per calcolare più trasformazioni contemporaneamente. Ad esempio, è possibile creare una singola matrice per tradurre e ruotare una serie di punti.
Le matrici vengono scritte in ordine di colonna di riga. Una matrice che ridimensiona uniformemente i vertici lungo ogni asse, noto come scala uniforme, è rappresentata dalla matrice seguente usando la notazione matematica.

In C++, Direct3D dichiara matrici come matrice bidimensionale, usando una struttura di matrice. Nell'esempio seguente viene illustrato come inizializzare una struttura D3DMATRIX per fungere da matrice di scalabilità uniforme (fattore di scala "s").
D3DMATRIX scale = {
5.0f, 0.0f, 0.0f, 0.0f,
0.0f, 5.0f, 0.0f, 0.0f,
0.0f, 0.0f, 5.0f, 0.0f,
0.0f, 0.0f, 0.0f, 1.0f
};
Traduci
L'equazione seguente converte il punto (x, y, z) in un nuovo punto (x', y', z').
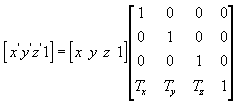
È possibile creare manualmente una matrice di traslazione in C++. Nell'esempio seguente viene illustrato il codice sorgente di una funzione che crea una matrice per convertire i vertici.
D3DXMATRIX Translate(const float dx, const float dy, const float dz) {
D3DXMATRIX ret;
D3DXMatrixIdentity(&ret);
ret(3, 0) = dx;
ret(3, 1) = dy;
ret(3, 2) = dz;
return ret;
} // End of Translate
Scala
L'equazione seguente ridimensiona il punto (x, y, z) in base a valori arbitrari nelle direzioni x, y e z in un nuovo punto (x', y', z').
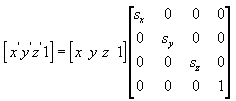
Ruota
Le trasformazioni descritte di seguito sono destinate a sistemi di coordinate sinistrorse, quindi possono essere diverse dalle matrici di trasformazione viste altrove.
L'equazione seguente ruota il punto (x, y, z) attorno all'asse x, producendo un nuovo punto (x', y', z').
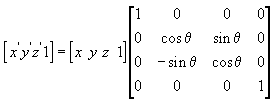
L'equazione seguente ruota il punto attorno all'asse y.
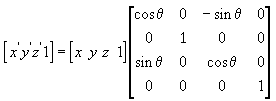
L'equazione seguente ruota il punto attorno all'asse z.
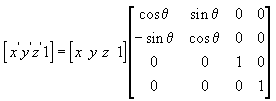
In queste matrici di esempio, la lettera greca theta sta per l'angolo di rotazione, in radianti. Gli angoli vengono misurati in senso orario quando si guarda lungo l'asse di rotazione verso l'origine.
Il codice seguente illustra una funzione per gestire la rotazione sull'asse X.
// Inputs are a pointer to a matrix (pOut) and an angle in radians.
float sin, cos;
sincosf(angle, &sin, &cos); // Determine sin and cos of angle
pOut->_11 = 1.0f; pOut->_12 = 0.0f; pOut->_13 = 0.0f; pOut->_14 = 0.0f;
pOut->_21 = 0.0f; pOut->_22 = cos; pOut->_23 = sin; pOut->_24 = 0.0f;
pOut->_31 = 0.0f; pOut->_32 = -sin; pOut->_33 = cos; pOut->_34 = 0.0f;
pOut->_41 = 0.0f; pOut->_42 = 0.0f; pOut->_43 = 0.0f; pOut->_44 = 1.0f;
return pOut;
}
Concatenazione di matrici
Uno dei vantaggi dell'uso delle matrici è che è possibile combinare gli effetti di due o più matrici moltiplicandoli. Ciò significa che, per ruotare un modello e convertirlo in una posizione, non è necessario applicare due matrici. Si moltiplicano invece le matrici di rotazione e traslazione per produrre una matrice composita contenente tutti i relativi effetti. Questo processo, denominato concatenazione matrice, può essere scritto con l'equazione seguente.
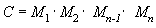
In questa equazione C è la matrice composita creata e M₁ tramite Mn sono le singole matrici. Nella maggior parte dei casi, vengono concatenate solo due o tre matrici, ma non esiste alcun limite.
L'ordine in cui viene eseguita la moltiplicazione della matrice è fondamentale. La formula precedente riflette la regola da sinistra a destra della concatenazione della matrice. Ovvero, gli effetti visibili delle matrici usate per creare una matrice composita si verificano in ordine da sinistra a destra. Nell'esempio seguente viene illustrata una tipica matrice globale. Supponiamo di creare la matrice globale per uno stereotipico sugo volante. Probabilmente l'intento è di ruotare il sugo volante intorno al suo centro, l'asse y dello spazio del modello, e convertirlo in un'altra posizione nella scena. Per ottenere questo effetto, creare prima una matrice di rotazione e quindi moltiplicarla per una matrice di traslazione, come illustrato nell'equazione seguente.
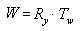
In questa formula, Ry è una matrice per la rotazione sull'asse y e Tw è una traslazione in una posizione nelle coordinate globali.
L'ordine in cui si moltiplicano le matrici è importante perché, a differenza della moltiplicazione di due valori scalari, la moltiplicazione della matrice non è commutativa. La moltiplicazione delle matrici nell'ordine opposto ha l'effetto visivo della conversione del sugo volante nella sua posizione spaziale globale e quindi ruotandola intorno all'origine mondiale.
Indipendentemente dal tipo di matrice che si sta creando, ricordare la regola da sinistra a destra per assicurarsi di ottenere gli effetti previsti.
Argomenti correlati