Transformations (Direct3D 9)

La partie de Direct3D qui envoie la géométrie via le pipeline geometry de fonction fixe est le moteur de transformation. Il localise le modèle et la visionneuse dans le monde, projette les sommets à afficher à l’écran et les clipse sur la fenêtre d’affichage. Le moteur de transformation effectue également des calculs d’éclairage pour déterminer les composants diffus et spéculaires à chaque sommet.

Le pipeline geometry prend des sommets comme entrée. Le moteur de transformation applique le monde, la vue et les transformations de projection aux sommets, clipse le résultat et transmet tout au rastériseur.

En tête du pipeline, les sommets d’un modèle sont déclarés par rapport à un système de coordonnées local. Il s’agit d’une origine locale et d’une orientation. Cette orientation des coordonnées est souvent appelée espace de modèle, et les coordonnées individuelles sont appelées coordonnées de modèle.

La première étape du pipeline geometry transforme les sommets d’un modèle de leur système de coordonnées local en un système de coordonnées utilisé par tous les objets d’une scène. Le processus de réorientation des sommets est appelé la transformation du monde. Cette nouvelle orientation est communément appelée espace mondial, et chaque sommet de l’espace mondial est déclaré à l’aide de coordonnées mondiales.

Dans l’étape suivante, les sommets qui décrivent votre monde 3D sont orientés par rapport à une caméra. Autrement dit, votre application choisit un point de vue pour la scène, et les coordonnées de l’espace monde sont déplacées et pivotées autour de la vue de la caméra, transformant l’espace du monde en espace de caméra. Il s’agit de la transformation d’affichage.

L’étape suivante est la transformation de projection. Dans cette partie du pipeline, les objets sont généralement mis à l’échelle en fonction de leur distance par rapport à la visionneuse afin de donner l’illusion de profondeur à une scène ; les objets fermés sont faits pour apparaître plus grands que les objets distants, et ainsi de suite. Par souci de simplicité, cette documentation fait référence à l’espace dans lequel les sommets existent après la transformation de projection en tant qu’espace de projection. Certains livres graphiques peuvent faire référence à l’espace de projection en tant qu’espace homogène post-perspective. Toutes les transformations de projection ne mettez pas à l’échelle la taille des objets dans une scène. Une telle projection est parfois appelée projection affine ou orthogonale.

Dans la dernière partie du pipeline, tous les sommets qui ne seront pas visibles à l’écran sont supprimés, afin que le rastériseur ne prenne pas le temps de calculer les couleurs et l’ombrage pour quelque chose qui ne sera jamais vu. Ce processus est appelé découpage. Après le découpage, les sommets restants sont mis à l’échelle en fonction des paramètres de la fenêtre d’affichage et convertis en coordonnées d’écran. Les sommets résultants, visibles à l’écran lorsque la scène est rastérisée, existent dans l’espace de l’écran.

Les transformations sont utilisées pour convertir la géométrie d’objet d’un espace de coordonnées à un autre. Direct3D utilise des matrices pour effectuer des transformations 3D. Cette section explique comment les matrices créent des transformations 3D, décrit certaines utilisations courantes des transformations et décrit en détail comment combiner des matrices pour produire une matrice unique qui englobe plusieurs transformations.

• Transformation mondiale (Direct3D 9) : convertir de l’espace de modèle en espace mondial
• Transformation d’affichage (Direct3D 9) : convertir de l’espace du monde en espace d’affichage
• Transformation de projection (Direct3D 9) : conversion de l’espace de vue en espace de projection

Transformations de matrice

Dans les applications qui fonctionnent avec des graphiques 3D, vous pouvez utiliser des transformations géométriques pour effectuer les opérations suivantes :

• Exprimer l’emplacement d’un objet par rapport à un autre objet.
• Faire pivoter et dimensionner des objets.
• Modifier les positions d’affichage, les directions et les perspectives.

Vous pouvez transformer n’importe quel point (x,y,z) en un autre point (x', y', z') à l’aide d’une matrice 4x4, comme illustré dans l’équation suivante.

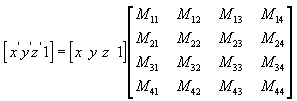
Effectuez les équations suivantes sur (x, y, z) et la matrice pour produire le point (x', y', z').

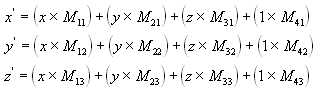
Les transformations les plus courantes sont la traduction, la rotation et la mise à l’échelle. Vous pouvez combiner les matrices qui produisent ces effets en une seule matrice pour calculer plusieurs transformations à la fois. Par exemple, vous pouvez créer une matrice unique pour traduire et faire pivoter une série de points.

Les matrices sont écrites dans l’ordre des colonnes de ligne. Une matrice qui met à l’échelle uniformément les sommets le long de chaque axe, appelée mise à l’échelle uniforme, est représentée par la matrice suivante à l’aide de la notation mathématique.

En C++, Direct3D déclare les matrices en tant que tableau à deux dimensions, à l’aide de la structure D3DMATRIX . L’exemple suivant montre comment initialiser une structure D3DMATRIX pour agir comme une matrice de mise à l’échelle uniforme.

// In this example, s is a variable of type float.

D3DMATRIX scale = {
    s,               0.0f,            0.0f,            0.0f,
    0.0f,            s,               0.0f,            0.0f,
    0.0f,            0.0f,            s,               0.0f,
    0.0f,            0.0f,            0.0f,            1.0f
};

Translate

L’équation suivante traduit le point (x, y, z) en nouveau point (x', y', z').

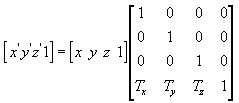
Vous pouvez créer manuellement une matrice de traduction en C++. L’exemple suivant montre le code source d’une fonction qui crée une matrice pour traduire les sommets.

D3DXMATRIX Translate(const float dx, const float dy, const float dz) {
    D3DXMATRIX ret;

    D3DXMatrixIdentity(&ret);
    ret(3, 0) = dx;
    ret(3, 1) = dy;
    ret(3, 2) = dz;
    return ret;
}    // End of Translate

Pour plus de commodité, la bibliothèque d’utilitaireS D3DX fournit la fonction D3DXMatrixTranslation .

Scale

L’équation suivante met à l’échelle le point (x, y, z) en fonction de valeurs arbitraires dans les directions x, y et z vers un nouveau point (x', y', z').

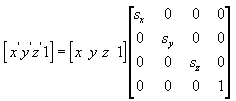
Faire pivoter

Les transformations décrites ici concernent les systèmes de coordonnées gauchers et peuvent donc être différentes des matrices de transformation que vous avez vues ailleurs.

L’équation suivante fait pivoter le point (x, y, z) autour de l’axe des x, produisant un nouveau point (x', y', z').

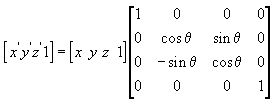
L’équation suivante fait pivoter le point autour de l’axe y.

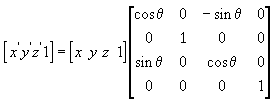
L’équation suivante fait pivoter le point autour de l’axe z.

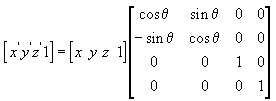
Dans ces exemples de matrices, la lettre grecque ntta représente l’angle de rotation, en radians. Les angles sont mesurés dans le sens des aiguilles d’une montre lorsque vous regardez le long de l’axe de rotation vers l’origine.

Dans une application C++, utilisez les fonctions D3DXMatrixRotationX, D3DXMatrixRotationY et D3DXMatrixRotationZ fournies par la bibliothèque d’utilitaires D3DX pour créer des matrices de rotation. Voici le code de la fonction D3DXMatrixRotationX .

D3DXMATRIX* WINAPI D3DXMatrixRotationX
    ( D3DXMATRIX *pOut, float angle )
{
#if DBG
    if(!pOut)
        return NULL;
#endif

    float sin, cos;
    sincosf(angle, &sin, &cos);  // Determine sin and cos of angle

    pOut->_11 = 1.0f; pOut->_12 =  0.0f;   pOut->_13 = 0.0f; pOut->_14 = 0.0f;
    pOut->_21 = 0.0f; pOut->_22 =  cos;    pOut->_23 = sin;  pOut->_24 = 0.0f;
    pOut->_31 = 0.0f; pOut->_32 = -sin;    pOut->_33 = cos;  pOut->_34 = 0.0f;
    pOut->_41 = 0.0f; pOut->_42 =  0.0f;   pOut->_43 = 0.0f; pOut->_44 = 1.0f;

    return pOut;
}

Matrices de concaténation

L’un des avantages de l’utilisation de matrices est que vous pouvez combiner les effets de deux matrices ou plus en les multipliant. Cela signifie que pour faire pivoter un modèle et le traduire à un emplacement donné, vous n’avez pas besoin d’appliquer deux matrices. Au lieu de cela, vous multipliez les matrices de rotation et de traduction pour produire une matrice composite qui contient tous leurs effets. Ce processus, appelé concaténation matricielle, peut être écrit avec l’équation suivante.

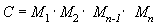
Dans cette équation, C est la matrice composite en cours de création, et M₁ à Mn sont les matrices individuelles. Dans la plupart des cas, seules deux ou trois matrices sont concaténées, mais il n’y a pas de limite.

Utilisez la fonction D3DXMatrixMultiply pour effectuer la multiplication matricielle.

L’ordre dans lequel la multiplication matricielle est effectuée est crucial. La formule précédente reflète la règle de gauche à droite de la concaténation matricielle. Autrement dit, les effets visibles des matrices que vous utilisez pour créer une matrice composite se produisent dans l’ordre de gauche à droite. Une matrice mondiale typique est illustrée dans l’exemple suivant. Imaginez que vous créez la matrice mondiale pour une soucoupe volante stéréotypée. Vous voudriez probablement faire tourner la soucoupe volante autour de son centre - l’axe y de l’espace de modèle - et le traduire à un autre emplacement dans votre scène. Pour accomplir cet effet, vous devez d’abord créer une matrice de rotation, puis la multiplier par une matrice de traduction, comme indiqué dans l’équation suivante.

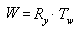
Dans cette formule, R_y est une matrice de rotation autour de l’axe y, et T_w est une traduction vers une position quelconque dans les coordonnées du monde.

L’ordre dans lequel vous multipliez les matrices est important, car, contrairement à la multiplication de deux valeurs scalaires, la multiplication de matrice n’est pas commutative. La multiplication des matrices dans l’ordre inverse a pour effet visuel de traduire la soucoupe volante à sa position spatiale mondiale, puis de la faire pivoter autour de l’origine du monde.

Quel que soit le type de matrice que vous créez, n’oubliez pas la règle de gauche à droite pour vous assurer que vous obtenez les effets attendus.

Rubriques connexes

Prise en main